Gukov on categorification and gauge theory

Between conferences, (because two weeks worth of talks on the week days just wasn’t enough) Sergei Gukov is giving some talks on categorification and gauge theory. Today, we had about 3 hours of talks, which I mostly thought were good, though I’m blanking a little on their content.

Unfortunately, they were somewhat marred by slightly excessive (in my opinion) audience participation. It’s one thing as an audience to ask the speaker to stop an explain something for fully. It’s another to derail the talk for 10 minutes in an attempt to change the topic of the talk.

Anyways, the content was roughly as follows:

Inspired by mathematical physics, people (mostly Witten, but with plenty of others involved) have written down certain gauge theories for 4-manifold, by which I mean a Lagrangian on the space of connections of any principal bundle P over your 4-manifold X, possibly also using extra data, such as a section of the positive spinor bundle (as in the case of Seiberg-Witten theory, perhaps the most famous of these gauge theories) along with the action of gauge symmetries (this is the automorphism gorup of the principal bundle, that is, just smooth sections of G\times X.

You use this Lagrangian to construct a measure on the space of connections (in a very non-rigorous way, but that shouldn’t worry about this for now, since we won’t actually compute any integrals of these). As your parameter \hbar goes to 0, this measure becomes more and more concentrated on the locus where the Lagrangian has a critical point, which turns out to be the set of solutions to a particular differential equation. If you start with the Chern-Simons Lagrangian (this is in 3 dimensions), you end up with the space of flat connections on your 3-manifold. If you do Donaldson theory, (now we’re back in 4-d) you end up with the set of anti-self dual connections on your principal bundle. If you start with Seiberg-Witten theory, you get solutions to the “monopole equations.”

Now, if you quotient out by the action of your gauge symmetries, you end with a space \mu(X) that can be surprisingly nice, usually finite-dimensional, sometimes compact, sometimes smooth, sometimes with more exciting structures, such as symplectic, complex, or hyperkähler ones, which (if you like using confusing physics terminology) you might call “the moduli space of monopoles.”

If you have a 2-manifold S or 3-manifold M, you do dimensional reduction, by taking the product with \mathbb{R}^2 or \mathbb{R} and look at the space of invariant solutions (you also want some kind of vanishing along fibers. I’ll admit, I didn’t quite understand this part), to get a couple of new moduli spaces \mu(S\times\mathbb{R}^2),\mu(M\times\mathbb{R}).

So what does this have to do with categorification? Well, it’s not 100% clear yet. We basically got as far as the list:

closed 4-manifold X\leadsto goes to a -1-category \chi(\mu(X))

closed 3-manifold goes to a 0-category H^*(\mu(M\times\mathbb{R}))

closed 2-manifold goes to a 1-category D^b(\mathrm{Coh}(\mu(S\times\mathbb{R}^2))

so associated to a TQFT, we have a hierarchy of categories. Hopefully, we’ll find out a little more about this tomorrow.

I think the most interesting thing I actually learned was the following somewhat remarkable theorem.

Theorem. Let X be holomorphic symplectic, and let L_1,L_2 Lagrangian holomorphic submanifolds. Then \mathrm{Ext}^\bullet(\mathcal{O}_{L_1} , \mathcal{O}_{L_2}) is naturally isomorphic to the symplectic Floer homology HF^{symp}(L_1,L_2).

Maybe the rest of you aren’t too impressed, but I think this is awesome. It makes me want to go compute intersections between core components of hypertoric varieties. But, instead I’m gonna go sleep.

10 thoughts on “Gukov on categorification and gauge theory”

  2. In the theorem you state, this is an isomorphism as what?
    I don’t understand Floer homology, but if this is just a statement about graded vector spaces it just says that HF(L1,L2) counts intersection points of the Lagrangians (at least after perturbation), no? (which I think is the def. of the morphism spaces in the Fukaya category?) But I guess the problem is that the compositions on the HF’s is not the same as composition of Exts, but involves various discs, in
    particular it is not local at the intersections, right?

  3. Isomorphisms as graded vector spaces.

    It’s true that this statement is easier and has less content than it appears at first, but you either missed a subtlety or are experienced enough with Floer homology it didn’t seem subtle to you. Floer homology is intersection points modulo a bunch of differentials coming from pseudoholomorphic disks which are really hard to count. This theorem says that you don’t have to worry about those if everything is also holomorphic.

  4. Ah right, forgot about the differential (first product)..
    so I guess the statement is there are no quantum corrections coming from two-pointed discs in this case.. cool, thanks.

  5. Did anyone in that talk really say what a (-1)-category is?

    It should be the set \{ \mathrm{true}, \mathrm{false}\}, since that’s the Hom-think of a 0-category.

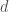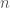    And that makes sense: a d-dimensional extended QFT should assign a (d - n - 1)-category of sections of a (d - n)vector bundle to n-dimensional parts of parameter space.

    So at top level we get a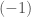 (-1)-category of sections of a 0-vector bundle. A 0-vector bundle is just a function. It has a section if that function is constant. More generally, it has a local section over each subset over which the function is constant.

    It looks to me like “taking the space of (-1)-sections” might hence actually have to be thought of as corresponding to the procedure Lebesgue integration of the corresponding function. #.

  8. I just meant a number (just on the logic “if you decategorify a set, you get a number”).

    Okay, I see. Thanks.

    I was just asking since

    a) in the Baez-ian school there is an attempt to give a precise meaning to the term “(-1)-category” and “(-2)-category” using the logic (alternative to the one you mention), that an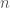 n-category is what a (n+1)-category is enriched over. 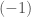Since a set can be regarded as a category enriched over truth values (either there is precisely one morphism between two elements (the identity if both are equal) or there is none), this makes a (-1)-category a truth value.

    b) Something subtle is apparently going on at top level for extended QFTs, concerning the conceptual underpinning (even though it may seem at first sight that top level is easiest, since numbers are easier than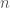 n-categories). It seems as if things in QFT might look more natural, conceptually, if there were a hidden categorical layer which we are missing so far, such that the true value of an extended QFT at top level becomes in fact a 0-category.

  9. Pingback: Not Even Wrong » Blog Archive » Too Much Good Stuff ~

  10. A little more comment/question about the statement of the equality of HF(L_1, L_2) and Ext(O_{L_1}, O_{L_2}). One day last year, I burst into Denis Auroux’s office with this question and we spent some time hashing it out. The idea is that both are isomorphic to H*(L_1 \cap L_2). On the algebraic side, the proof is to go local to global. On the symplectic side, the idea is as Ben mentioned that the fact that L_1, L_2 are holomorphic Lagrangians allows one to control the pseudoholomorphic disks — Denis did give me a nice argument for this which I now forget. (by the way, this was the beginning of the work with Sabin)

    Anyway, the real reason for this post is to ask if anyone know a place where the proof of this theorem is written down?

    (btw, I am back from Japan and soon I will probably make a real post to this blog)

Comments are closed.