Conference on Higher Gauge Theory, Quantum Gravity, and Topological Field Theory

In February there is going to be a workshop and school dedicated to exploring the interactions of Quantum Gravity, Higher Gauge Theory, and Topological Field Theory. I’m excited about the chance to share ideas and hopefully create some new mathematics.

The conference will take place in Lisbon, Portugal, and yours truly will be giving one of the mini-courses for the school (the topic is going to be the classification of extended 2D tqfts, something near and dear to my heart). Of course that makes me really excited, but I am also excited about the other topics too and I think the mix of ideas will be invigorating. For more info look below the break.

New Journal: Quantum Topology

The European Math Society Publishing House (a non-profit publishing company which also publishes the Journal of the EMS, CMH, and half a dozen other journals) just announced a new journal: Quantum Topology. I think this is very exciting as it fills a nice hole in the existing journal options. The list of main topics include knot polynomials, TQFT, fusion categories, categorification, and subfactors. So there should be lots of material of interest to people here.

Extended TFTs

So I’ve finally managed to bang my dissertation into something more or less ready for public consumption. It is basically finished (except for some typos and spell checking).

It is available on my new website.

The title is “The Classification of Two-Dimensional Extended Topological Field Theories”.

Tikz, Slides, and Dissertations

There has been some recent discussion about tikz and beamer and I wanted to throw my two cents into the mix. What better way then by showing off the slides I used last week to talk about my dissertation? I had a lot of pictures, all of which I made entirely in tikz. Here is the link.

Lurie on TFTs

This morning Jacob Lurie posted a draft of an expository paper on his work (with Mike Hopkins) classifying extended (infinity, n)-categorical topological field theories and their relation to the Baez-Dolan cobordism hypothesis.

Should make for some intersting bedtime reading…

TQFTs via Planar Algebras (Part 3)

This is the third and final post in my series about using planar algebras to construct TQFTs. In the first post we looked at the 2D case and came up with a master strategy for constructing TQFTs. In the last post we began carrying out that strategy in the 3-dimensional setting, but ran into some difficulties. In this post we will overcome those difficulties and build a TQFT.

TQFTs via Planar Algebras (Part 2)

In my last post I explained a strategy for using n-dimensional algebraic objects to construct (n+1)-dimensional TQFTs, and I went through the n=1 case: Showing how a semi-simple symmetric Frobenius algebra gives rise to a 2-dimensional TQFT. But then I had to disappear and go give my talk. I didn’t make it to the punchline, which is how planar algebras can give rise to 3D TQFTs!

In this post I will start explaining the 3D part of the talk. I won’t be able to finish before I run out of steam; that will have to wait for another post. But I will promise to use lots of pretty pictures!

TQFTs via Planar Algebras

So today I am giving a talk in the Subfactor seminar here at Berkeley, and I thought it might by nice to write my pre-talk notes here on the blog, rather then on pieces of paper destined for the recycling bin.

This talk is about how you can use Planar algebras planar techniques to construct 3D topological quantum field theories (TQFTs) and is supposed to be introductory. We’ve discussed planar algebras on this blog here and here.

So the first order of buisness: What is a TQFT?

New Photograph

Last Friday, we had a seminar at Berkeley — or rather, at Noah’s house — featuring Mike Freedman and some quantity of beer. Mike spoke about some of the hurdles he had to overcome in writing his recent paper with Danny Calegari and Kevin Walker. One of the main results of this paper is that there is a “complexity function” c, which maps from the set of closed 3-manifolds to an ordered set, and that this function satisfies the “topological” Cauchy-Schwarz inequality.

Here, and are 3-manifolds with boundary . [EDIT: and equality is only achieved if ] This inequality looks like the sort of things you might derive from topological field theory, using the fact that . Unfortunately, it’s difficult to actually derive this sort of theorem from any well-understood TQFT, thanks to an old theorem of Vafa’s, which states roughly, that there’s always two 3-manifolds related by a Dehn twist that a given rational TQFT can’t distinguish. Mike speculated that non-rational TQFT might be able to do the trick, but what he and his collaborators actually did was an end run around the TQFT problem. They simply proved that that the function exists.

I tell you all this, not because I’m about to explain what is, but to explain our new banner picture. We realized after the talk that there were a fair number of us Secret Blogging Seminarians in one place, and that we ought to take a photo.

Geometric Langlands from a TQFT perspective

In my continuing attempts to clear the backlog in my brain, I would like to tell you about the talks of Nadler and Gukov from Miami workshop which I was at a month ago. (Actually I really want to tell you about Kontsevich’s talks but I don’t think that I understand them well enough to do that.)

Ever since the work of Kapustin and Witten a couple of years ago, a TQFT interpretation of geometric Langlands has been available. However, I had never “internalized” it until these talks. It gives a nice conceptual picture which makes some constructions in geometric Langlands less mysterious and hopefully makes the whole subject a bit more accessible.

In this view of things, geometric Langlands concerns the equality of two 4D TQFTs, which will denote by A and B. A and B both depend on the choice of a semisimple algebraic group G. Or more precisely, if we want A = B, then we should have A depending on G and B depending on its Langlands dual group . They are 4D TQFTs, so they assign a number to a (closed) 4-manifold, a vector space to a 3-manifold, a category to a 2-manifold etc and related morphisms to bordisms of such objects.

I will start with a 2-manifold C. The first surprise is that A(C) and B(C) depend on more than just a topological structure for C — in particular we assume that C is actually endowed with the structure of smooth projective algebraic curve. Then we define and . Here 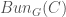is the moduli space of algebraic principal G bundles on C and 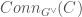is the moduli space of algebraic principal bundles with connection on C. To continue the explanation, D-mod means the category of modules for the sheaf of differential operators (equivalently the category of perverse sheaves) and QCoh means the category of quasi-coherent sheaves.