The decline of quantum algebra (QA)

I was browsing through different category listings on the arXiv today and noting the changes in numbers of papers over the years. As you might expect, there are more and more papers being posted to the arXiv every year. However, one category defies this trends: QA (quantum algebra).

There are actually less papers being posted to QA in the past three years (2010 317, 2009 308, 2008 323), than there were in the late 90s (1998 364, 1997 434, 1996 395). By contrast, there are about 4 times as many AG papers in the past few years compared to the late 90s, about 10 times as many RT papers, and about 5 times as many GT papers.

What do you make of this? Does it represent a trend in the kind of math that people are doing? Or are people just classifying their work differently?

It would be interesting to see if one can use this arXiv category to get a sense of which fields are becoming more and less popular over time.

Passage from compact Lie groups to complex reductive groups

Once again, I’m preparing to teach a class and needing some advice concerning an important point. I’m teaching a course of representation theory as a followup to an excellent course on compact Lie groups, taught this semester by Eckhard Meinrenken. In my class, I would like to explain transition from compact Lie groups to complex reductive groups, as a first step towards the Borel-Weil theorem.

A priori, compact connected Lie groups and complex reductive groups, seem to have little in common and live in different worlds. However, there is a 1-1 correspondence between these objects — for example and are related by this correspondence. Surprisingly, it is not that easy to realize this correspondence.

Let us imagine that we start with a compact connected Lie group and want to find the corresponding complex algebraic group . I will call this process complexification.

One approach to complexification is to first show that is in fact the real points of a real reductive algebraic group. For any particular this is obvious — for example 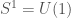is described by the equation . But one might wonder how to prove this without invoking the classification of compact Lie groups. I believe that one way to do this is to consider the category of smooth finite-dimensional representation of the group and then applying a Tannakian reconstruction to produce an algebraic group. This is a pretty argument, but perhaps not the best one to explain in a first course. A slightly more explicit version would be to simply define to b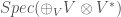e where ranges over the irreducible complex representations of 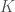(the Hopf algebra structure here is slightly subtle).

In fact, not only is every compact Lie group real algebraic, but every smooth map of compact Lie groups is actually algebraic. So the
the category of compact Lie groups embeds into the category of real algebraic groups. For a precise statement along these lines, see this very well written
MO answer by BCnrd.

A different approach to complexification is pursued in
Allen Knutson’s notes and in Sepanski’s book. Here the complexification of 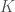is defined to be any such that there is an embedding , such that on Lie algebras 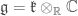. (Actually, this is Knutson’s definition, in Sepanski’s definition we first embed 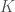into .) This definition is more hands-on, but it is not very obvious why such is unique, without some structural theorems describing the different groups with Lie algebra .

At the moment, I don’t have any definite opinion on which approach is more mathematically/pedagogically sound. I just wanted to point out something which I have accepted all my mathematical life, but which is still somewhat mysterious to me. Can anyone suggest any more a priori reasons for complexification?

Wanted: page of tax info for NSF fellows

So I think something that the world needs is a page with important bits of knowledge and tricks concerning having an NSF graduate or postdoctoral fellowship and paying taxes. The somewhat tricky thing is that you’d need an actual lawyer involved at some point in the process. Is this something one could try to convince the NSF’s accounting department to do? Presumably it’d be easy for the right person to do, and would save a lot of time for NSF Fellows who could then do math instead of trying to figure out taxes.

Here’s some examples of the sort of questions this page could answer:

• In what ways is NSF income taxable? (My understanding, which is not legal tax advice, is that you must pay income tax on this money by writing “SCH $$$” on the dotted line next to box 7, but you do not need to file a Schedule C nor a Schedule SE nor pay FICA/self-employment tax.)
• Is it possible to efile when you have taxable scholarship and fellowship income? Or do you have to print out the form in order to write “SCH $$$” on the dotted line next to box 7? (The rumor in the dept. today was that someone knew how to get TurboTax to enter the SCH thing, but none of us actually there knew.)
• How is the “research allowance” treated? My understanding, which again is not tax advice, is that since this is only for reimbursement it is not income.
• How are health care costs treated? At Columbia they apparently treat your health care as taxable income issuing you a 1099-MISC for non-employee compensation. This seems contrary to my readings of both the 1099-MISC instructions (where one of the criteria for issuing a 1099-MISC is that there were services rendered) and to section III.B.3. of the NSF Postdoctoral Fellowship Solicitation. But presumably Columbia’s accountants know what they’re doing. Nonetheless it’s extremely difficult to figure out what this money means. Is it FICA taxable? Do I have to file a Schedule C? What are my business expenses if it’s a business that didn’t actually do anything but yet was given money for no reason and then spent all its money on my healthcare? Why didn’t Berkeley issue me a 1099-MISC for the portion of my fees that went to medical care in graduate school? Is it possible to know in advance which schools treat health insurance money this way? If it’s self-employment money then I could wind up paying 15% FICA + 9% State and City + 25% Federal of $6K because of Columbia’s accounting.

Anyone have other good questions? Know anywhere to find answers to these questions?

When fine just ain’t enough

If you use sheaves to study differential geometry, one of the basic lemmas you’ll want is the following: Let be a smooth manifold and let be a sheaf of modules over . (For example, might be the sheaf of sections of a vector bundle.) Then all higher sheaf cohomology of vanishes.

The proof of this theorem is basically homological algebra plus the existence of partitions of unity. This gives rise to a slogan “when you have partitions of unity, sheaf cohomology vanishes.” One way to make this definition precise is through the technology of fine sheaves.

As Wikipedia says today, “[f]ine sheaves are usually only used over paracompact Hausdorff spaces”. That means they are not used when working with the Zariski topology on schemes, for example. When I started digging into this, I realized there were good reasons: The technology of fine sheaves (and the closely related technology of soft sheaves) does not include the scheme theory cases which we would want it to.

However, there are theorems of the form “when you have partitions of unity, sheaf cohomology vanishes” on schemes and on complex manifolds. I put up a question at MathOverflow asking whether there were better formulations that included these examples, but I probably didn’t formulate it well. I think spelling out all my issues would be too discursive for MathOverflow, so I’m bringing it over here.

Rhombus tilings and an over-constrained recurrence

I recently visited Robin Pemantle and his student Peter Du at UPenn. We talked about tilings of planar regions, generating functions and asymptotics. Towards the end, we talked about a bit about a very classical example, which is what I want to tell you about today.

In most planar tiling problems, the goal is an asymptotic analysis for tilings of large regions, because there isn’t enough structure to do better. This is the approach taken in the beautiful work of Kenyon, Okounkov, and collaborators.^{1, 2, 3} Sometimes, there is enough structure to give exact solutions with explicit generating functions. This is the situation with Aztec Diamonds, fortresses, and other several other examples.^4,5 The central name here is Jim Propp 6, 7, who has developed this theory together with many undergraduate and graduate students (including me).

And then there is one case: rhombus tilings of a hexagon. These have almost too much structure; more structures than one would expect to be compatibly possible. In this post, I want to talk about this example. In particular, I want to ask you a question which I thought about a bit on the train ride back and see whether any of you have some thoughts.

A (partial) explanation of the fundamental lemma and Ngo’s proof

I would like to take Ben up on his challenge (especially since he seems to have solved the problem that I’ve been working on for the past four years) and try to explain something about the Fundamental Lemma and Ngo’s proof.  In doing so, I am aided by a two expository talks I’ve been to on the subject — by Laumon last year and by Arthur this week.

Before I begin, I should say that I am not an expert in this subject, so please don’t take what I write here too seriously and feel free to correct me in the comments.  Fortunately for me, even though the Fundamental Lemma is a statement about p-adic harmonic analysis, its proof involves objects that are much more familiar to me (and to Ben).  As we shall see, it involves understanding the summands occurring in a particular application of the decomposition theorem in perverse sheaves and then applying trace of Frobenius (stay tuned until the end for that!).

First of all I should begin with the notion of “endoscopy”.  Let be two reductive groups and let be there Langlands duals.  Then is called an endoscopic group for if is the fixed point subgroup of an automorphism of .  A good example of this is to take , .  At first glance these groups having nothing to do with each other, but you can see they are endoscopic since their dual groups are and and we have .

As part of a more general conjecture called Langlands functoriality, we would like to relate the automorphic representations of to the automorphic representations of all possible endoscopic groups .  Ngo’s proof of the Fundamental Lemma completes the proof of this relationship.

Algebraic geometry without prime ideals

The first definition in “Grothendieck-style” algebraic geometry is the affine scheme for any ring . This is a topological space whose set of points in the set of prime ideals in . Then one defines a scheme to be a locally ringed space locally isomorphic to an affine scheme.

The definition of goes against intuition since it involves prime ideals, not just maximal ideals. Maximal ideals are more natural, since if for some alg closed field , then the set of maximal ideals of is in bijection with the vanishing set in the affine space of the ideal . (Of course one can give a geometric meaning to the prime ideals in terms of subvarieties, but it is less natural.)

However, in Daniel Perrin’s text Algebraic geometry, an introduction, he states/implies that one can define affine schemes just using maximal ideals (at least for finitely-generated algebras) and still get a good theory of schemes and varieties. Is this true?  If so why don’t we all learn it this way? (One answer to the this latter question could be that some people are interested in non-algebraically closed fields.)

Quaternions and Tensor Categories

As you can tell from the title of this post, I am trying to drag John Baez over to our blog.

Let be the ring of quaternions, i.e., with the standard relations. Let -mod be the category of left -modules. This has an obvious tensor structure (including duals), inherited from the category of vector spaces. Actually, that structure doesn’t quite work; I’ll leave to you good folks to work out what I should have said.

Let be a quaternion. Anyone who works with quaternions knows that there are two notions of trace. The naive trace, , is the trace of multiplication by on any irreducible -module, using the obvious tensor structure. But there is a better notion, the reduced trace, which is equal to . Similarly, there is a naive norm, , and there is a reduced norm .

This all makes me think that there is a subtle tensor category structure on -mod, other than the obvious one, for which these are the trace and norm in the categorical sense. Can someone spell out the details for me?

By the way, a note about why I am asking. I am reading Milne’s excellent notes on motives, and I therefore want to understand the notion of a non-neutral Tannakian category (page 10). As I understand it, this notion allows us to evade some of the standard problems in defining characteristic cohomology; one of which is the issue above about traces in quaternion algebras.

Combinatorial Question

Here’s something I can prove, but I don’t understand.

Let be the number of trees whose leaves are labeled by , and whose internal vertices all have degree . So counts objects like the tree on the right.

Let . Let be the number of pairings of . So counts objects like the pairing on the left.

Theorem: .

Proof: We have the recursive relations and . (Exercise!)

Of course, it is easy to solve these recursions and compute that . This is sequence A001147 in Sloane’s encyclopedia, the so-called double factorial sequence.

Now, let be the number of trivalent trees with vertices which can be embedded in a disc, with the leaves occurring in circular order on the boundary. And let be the number of pairings of which can be embedded in a disc, with the points occurring in circular order around the boundary. The figures below show that .

Theorem:

Proof: We have the recurrences and . (Exercise!)

These are, of course, the Catalan numbers (Sloane A000108). There is a closed formula, .

So the question is: Why? Is there some bijection between trees and matchings under which the condition of having a planar embedding behaves nicely? Are there other examples where we can go between double-factorial objects, with a symmetric group symmetry and Catalan objects with a dihedral symmetry?

Synergistic what?

So, I’m curious: what do those of you who are pretty vanilla mathematicians list as “synergistic activities” in your NSF bios? At the moment, all I’m coming up with is this blog.