Once again, I’m preparing to teach a class and needing some advice concerning an important point. I’m teaching a course of representation theory as a followup to an excellent course on compact Lie groups, taught this semester by Eckhard Meinrenken. In my class, I would like to explain transition from compact Lie groups to complex reductive groups, as a first step towards the Borel-Weil theorem.
A priori, compact connected Lie groups and complex reductive groups, seem to have little in common and live in different worlds. However, there is a 1-1 correspondence between these objects — for example and
are related by this correspondence. Surprisingly, it is not that easy to realize this correspondence.
Let us imagine that we start with a compact connected Lie group and want to find the corresponding complex algebraic group
. I will call this process complexification.
One approach to complexification is to first show that is in fact the real points of a real reductive algebraic group. For any particular
this is obvious — for example
is described by the equation
. But one might wonder how to prove this without invoking the classification of compact Lie groups. I believe that one way to do this is to consider the category of smooth finite-dimensional representation of the group and then applying a Tannakian reconstruction to produce an algebraic group. This is a pretty argument, but perhaps not the best one to explain in a first course. A slightly more explicit version would be to simply define
to be
where
ranges over the irreducible complex representations of
(the Hopf algebra structure here is slightly subtle).
In fact, not only is every compact Lie group real algebraic, but every smooth map of compact Lie groups is actually algebraic. So the
the category of compact Lie groups embeds into the category of real algebraic groups. For a precise statement along these lines, see this very well written
MO answer by BCnrd.
A different approach to complexification is pursued in
Allen Knutson’s notes and in Sepanski’s book. Here the complexification of is defined to be any
such that there is an embedding
, such that on Lie algebras
. (Actually, this is Knutson’s definition, in Sepanski’s definition we first embed
into
.) This definition is more hands-on, but it is not very obvious why such
is unique, without some structural theorems describing the different groups
with Lie algebra
.
At the moment, I don’t have any definite opinion on which approach is more mathematically/pedagogically sound. I just wanted to point out something which I have accepted all my mathematical life, but which is still somewhat mysterious to me. Can anyone suggest any more a priori reasons for complexification?
It seems to me that, from any of these perspectives, the hard part is to show that a compact Lie group has any nontrivial finite dimensional representations. In the Tannakian persective, how do you know the tensor category isn’t trivial; in Allen/Sepanski’s description, you define it in by assuming that has a unitary rep.
has a unitary rep.
What is the easiest way to get to this fact?
David- Isn’t any unitary irreducible of a compact group finite dimensional for simple topological reasons? Assuming that it’s easy; just decompose $L^2(G)$.
David – Any Lie group has an adjoint representation. If you want a faithful representation of a compact Lie group, take a direct sum of adjoint tensor central character for appropriate central characters.
Ben – I’m not sure about this simple topological reasons part, I thought you needed to use something like spectral theory of compact operators. eg, if is invariant under the adjoint action of G, then it is central, and acts by a compact operator on L^2(G). You find the irreps inside the finite-dimensional eigenspaces for non-zero eigenvectors.
is invariant under the adjoint action of G, then it is central, and acts by a compact operator on L^2(G). You find the irreps inside the finite-dimensional eigenspaces for non-zero eigenvectors.
@Ben Maybe? I don’t know the argument which you are sketching.
@Peter Isn’t there a difficult step being left out there, where you have to relate characters of the Lie algebra and characters of the group? It seems to me that, a priori, I could have![\mathfrak{g}/[\mathfrak{g}, \mathfrak{g}] = \mathbb{R}^n](https://s0.wp.com/latex.php?latex=%5Cmathfrak%7Bg%7D%2F%5B%5Cmathfrak%7Bg%7D%2C+%5Cmathfrak%7Bg%7D%5D+%3D+%5Cmathbb%7BR%7D%5En&bg=ffffff&fg=444444&s=0&c=20201002) for
for  , and yet
, and yet  .
.
The part of my comment that involves central characters is complete nonsense and I don’t know how to fix it.
comment that belongs on meta.sbseminar: Ben’s comment has no number!
a) There’s a subtlety you didn’t mention — there’s a unique _affine_ complexification. S^1 can be complexified to an elliptic curve. (I suppose R has two different complexifications too!)
b) Eckhard.
c) Ben’s numberless comment bugs me too!
d) Fixing the central characters argument would be much like proving Lie’s theorem, no?
About using L^2(G): part of the not-so-obvious part is to define L^2(G) and check that it _is_ a unitary representation… Constructing from scratch the Haar measure of a general compact group is not so easy. And even the continuity of the regular representation on L^2(G) is not purely formal.
Allen – Thanks for catching the spelling mistake.
As far as the affine property goes, I am using the (reasonably standard) terminology that algebraic group means affine algebraic group.
I’ve got a couple of naive questions about the relationship between these things.
a) What is the difference betweeen (1) the 2-category of connected compact Lie groups, and (2) the 2-category of connected complex reductive groups? (A 2-morphism between homomorphisms is given by conjugation by an element.) My guess is that they are nearly equivalent; but I’ve never seen anything like a precise statement. (They aren’t exactly equivalent; the center of $GL_n$ is bigger than the center of $U(n)$.)
b) What if we drop the condition that the groups be connected?
I hope you mean that its numberlessness bothers you, not its content (admittedly, its content is half-baked). When I’m in the WP dashboard, there’s a “reply” option to a comment which adds a numberless comment. I’m not sure what the point of not putting a number is. The point for me is to not to have to go to the page in order to add the comment.
Charles- If you consider the 2-categories where 1-morphisms are isomorphisms between semi-simple compact groups, and isomorphisms between semi-simple complex groups, then you get an equivalence. This is essentially just the fact that compact forms are self-normalizing. If you allow tori or non-isomorphisms, then this won’t work, since you have have non-compact normalizers to images of compact stuff in these situations.
Page 71 of J.P. Serre’s book “Complex Semisimple Lie Algebras” states: “the construction of the affine algebra $A_G$ of $G$ is easy: its elements are the continuous functions $f$ on $K$ whose translates span a finite dimensional vector space. Note that this algebra has a canonical real structure; it therefore defines an algebraic group $L$ over $\mathbb{R}$. The set of real points of $L$ is $K$; its set of complex points $G$.”
In Serre’s book, $K$ is assumed to have a semisimple Lie algebra, but does that matter?
Bart – Thanks for your comment. Serre’s construction is a nicer version of the construction , I mentioned in my post. This is because a function having a finite-dimensional translate is equivalent to it being the matrix coefficient of a finite-dimensional representation.
, I mentioned in my post. This is because a function having a finite-dimensional translate is equivalent to it being the matrix coefficient of a finite-dimensional representation.
I don’t believe that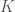 needs to be compact in this construction.
needs to be compact in this construction.
I guess I am agreeing now with David’s first comment that once you know that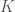 has lots of finite-dimensional representations, then it is not so hard to show that it is algebraic and has a complexification.
has lots of finite-dimensional representations, then it is not so hard to show that it is algebraic and has a complexification.
This suggests that there might be some way to directly prove the following theorem: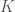 is a closed connected Lie subgroup of
is a closed connected Lie subgroup of  , then it is an algebraic subgroup, i.e. it is a (real) subvariety.
, then it is an algebraic subgroup, i.e. it is a (real) subvariety.
If
I really like the argument in the article on Tannaka duality by Joyal and Street because it really lets you separate out the part of the proof that is “purely formal” (in that it works not just for compact Lie groups but for arbitrary topological monoids), the part that relies crucially on analytic facts about compact groups, and the (extremely small!) part that actually requires the word “Lie.”
Here is a sketch of their proof. Given any topological monoid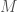 , one can form the following two gadgets. The Tannaka monoid
, one can form the following two gadgets. The Tannaka monoid  consists of those endomorphisms of the forgetful functor
consists of those endomorphisms of the forgetful functor  that are monoidal and self-conjugate. (It is straightforward to show that
that are monoidal and self-conjugate. (It is straightforward to show that  is a compact group for a compact group
is a compact group for a compact group  .) The algebra of representative functions
.) The algebra of representative functions  is the subalgebra of
is the subalgebra of  spanned by the matrix coefficients of representations. This is a bialgebra under the coproduct
spanned by the matrix coefficients of representations. This is a bialgebra under the coproduct  .
.
There’s a natural map , which corresponds to the evaluation. There’s also a natural map
, which corresponds to the evaluation. There’s also a natural map  coming from the action of
coming from the action of 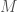 on representations. The map
on representations. The map  can be extended to an operator-valued Fourier transform
can be extended to an operator-valued Fourier transform  , which is an isomorphism of topological monoids.
, which is an isomorphism of topological monoids.
We’d like to show that is an isomorphism (this is Tannaka-Krein duality). This is not true in general, but when
is an isomorphism (this is Tannaka-Krein duality). This is not true in general, but when  is a compact group, we can bring all of our favorite analytic results to bear. Peter-Weyl immediately implies that
is a compact group, we can bring all of our favorite analytic results to bear. Peter-Weyl immediately implies that  is injective. Surjectivity is trickier, but it ultimately boils down to leveraging the orthogonality relations to show first that
is injective. Surjectivity is trickier, but it ultimately boils down to leveraging the orthogonality relations to show first that  induces an equivalence between the representation theories of
induces an equivalence between the representation theories of  and
and  and then that this forces the image of
and then that this forces the image of  to be all of
to be all of  .
.
The only bit that’s missing is showing that is finitely generated. This will be true if
is finitely generated. This will be true if  admits a faithful representation. For a compact Lie group, the set of kernels of representations has a minimal element (since they are closed submanifolds), so Peter-Weyl tells us that there’s a representation with zero kernel. (I suppose this also requires the fact that continuous maps between Lie groups are smooth.)
admits a faithful representation. For a compact Lie group, the set of kernels of representations has a minimal element (since they are closed submanifolds), so Peter-Weyl tells us that there’s a representation with zero kernel. (I suppose this also requires the fact that continuous maps between Lie groups are smooth.)
While this may not be the most accessible proof for a first course, it might be essentially the only way to do it that does not involve already knowing about the structure theory of reductive groups (for instance, to get the uniqueness statement in the Knutson/Sepanski approach you mention). I think this is the price for trying to remove the analytic parts of the proof; the idea of Tannaka duality should probably in principle underlie any proof of this result, and you have the option of doing it in the (hopefully) familiar compact setting or the unfamiliar algebraic setting.
[\operatorname seemed to be causing trouble; I changed them all to \mathrm . DES]
Dear Joel: If you look in Chapter 3 of Bourbaki LIE, they have a section on “complexification”. If $G$ is a connected real Lie group (in the smooth or real-analytic sense, say), one can consider morphisms from $G$ to the underlying real Lie group of a connected complex Lie group. They define a *complexification* of $G$ to be an initial such morphism, and prove that this always exists and has the expected Lie algebra (if I remember correctly). What they do not address is whether this is interesting in specific cases (e.g., no serious examples discussed), and they don’t address when the canonical map to the complexification has trivial kernel (need not). But one can give direct arguments (using facts about compact groups) to show that for compact $G$ it has trivial kernel. Although one doesn’t have a “complexification” operation on real-analytic manifolds akin to what one has on the algebraic side (where extension of scalars always makes sense), the Bourbaki viewpoint is a nice one (e.g., it is not ad hoc) provided that it is supplemented with finer results that address how it works out in various interesting cases (such as compact Lie groups).
@Brian: Your comment is apt, but keep in mind that the anonymous Bourbaki group hardly ever contaminated what they did by serious examples. At least their so-called exercises contain some examples, but their pure and often welcome rigorous theoretical viewpoint is uncompromised by the inconvenient question students usually ask: Why?
Constructing from scratch the Haar measure of a general compact group is not so easy.
Constructing it for compact Lie groups is, though. Pick a volume form at the origin, left-translate to get a left-invariant volume form, use it to define an orientation, integrate, get some finite positive number automagically. Rescale by that to get the left-invariant volume form of total volume 1.
Joel asks whether there is a direct proof of the following:
If is a closed connected Lie subgroup of
is a closed connected Lie subgroup of  , then it is an algebraic subgroup, i.e. it is a (real) subvariety.
, then it is an algebraic subgroup, i.e. it is a (real) subvariety.
I decided to give this a try this morning. Here is my best effort. I am missing the following lemma:
Lemma 1: A closed subgroup of is a smooth submanifold.
is a smooth submanifold.
Assuming that, here is the proof. Let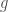 be an element of
be an element of  not in
not in  . Our goal is to construct a polynomial
. Our goal is to construct a polynomial 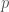 such that
such that  is
is 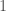 and
and  . This will present
. This will present  as an intersection of infinitely (even uncountable many) polynomials. One could then use a further argument to show that
as an intersection of infinitely (even uncountable many) polynomials. One could then use a further argument to show that  is a finite intersection of polynomials, but I won’t do that.
is a finite intersection of polynomials, but I won’t do that.
Let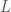 be the closure, in
be the closure, in  , of the subgroup generated by
, of the subgroup generated by  and
and 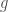 . So
. So 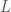 is a closed subgroup of
is a closed subgroup of  . Let
. Let  be the
be the  -dimensional representation
-dimensional representation  of U(n): the direct sum of the standard rep and its dual.
of U(n): the direct sum of the standard rep and its dual.
Lemma 2: Let be a chain of closed Lie subgroups of
be a chain of closed Lie subgroups of  . For
. For 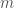 sufficiently large, there is a vector in
sufficiently large, there is a vector in  which is fixed by
which is fixed by  and not by
and not by 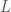 .
.
Proof: Let be the trace function on
be the trace function on  . The character of
. The character of  is then
is then  ; call this function
; call this function  . Note that
. Note that  , that
, that  everywhere else on
everywhere else on  , and that
, and that  drops off quadratically near the identity.
drops off quadratically near the identity.
The space of fixed vectors of
fixed vectors of  has dimension:
has dimension:  where
where  is Haar measure normalized to have volume
is Haar measure normalized to have volume 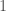 . For
. For 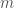 large, the dominant contribution to the integral is from a small neighborhood of the identity.
large, the dominant contribution to the integral is from a small neighborhood of the identity.
Let . Near the identity, this integral is well approximated by
. Near the identity, this integral is well approximated by
 .
. is a constant that’s hard to describe correctly.
is a constant that’s hard to describe correctly.
Here
If is greater than
is greater than  , then the space of fixed vectors for
, then the space of fixed vectors for 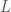 has dimension growing like
has dimension growing like  , which drops off faster than
, which drops off faster than  , so there is a vector fixed by
, so there is a vector fixed by  and not by
and not by 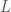 .
.
If and
and 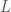 have the same dimension, let
have the same dimension, let  be the index of
be the index of  in
in 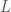 . Then
. Then  so, again, for
so, again, for 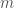 large, there are more vectors fixed by
large, there are more vectors fixed by  than by
than by 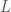 . QED
. QED
OK, that proves the lemma. Let be fixed by
be fixed by  and not by
and not by 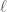 . So
. So  is not fixed by
is not fixed by 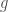 . Normalize
. Normalize  to have length 1. Let
to have length 1. Let  (the Hermitian inner product). Then
(the Hermitian inner product). Then 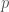 is
is 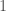 on
on  and not at
and not at 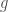 .
.
But, written out explicitly, is a polynomial in the entries of
is a polynomial in the entries of 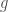 and their complex conjugates. And, since
and their complex conjugates. And, since 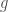 is unitary, the entries of
is unitary, the entries of  are polynomials in the entries of
are polynomials in the entries of 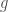 , and in
, and in  . Clearing out determinants from the denominator,
. Clearing out determinants from the denominator,  is distinguished from
is distinguished from 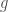 by a polynomial.
by a polynomial.
Wow, David. Nice argument. Just in time too (for my course).
The Lemma 1 you mention is a standard fact: see for example Brocker-tom Dieck Theorem 3.11.
What is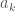 and how do you show the part about the integral being well-approximated?
and how do you show the part about the integral being well-approximated?
Here are the rough details. Since you are teaching the course, you get to find all the two’s and pi’s :).
Let K be a subgroup of U(n), with lie algebra . There are two reasonable volume forms on
. There are two reasonable volume forms on  . One is the Haar measure of
. One is the Haar measure of  , normalized to have integral
, normalized to have integral 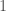 . The other is to take the standard Riemann metric on
. The other is to take the standard Riemann metric on  (translate the Killing form) and restrict it to
(translate the Killing form) and restrict it to  . A Riemann metric gives a natural volume form. The constant
. A Riemann metric gives a natural volume form. The constant  is the ratio of these two, or something like it. In particular, if
is the ratio of these two, or something like it. In particular, if  has finite index in
has finite index in 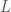 , then the forms gotten by restriction are the same. But the Haar measures obey
, then the forms gotten by restriction are the same. But the Haar measures obey  . So that’s why
. So that’s why  .
.
Now, approximating the integral. Choose small balls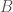 in
in  , and
, and 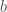 in
in  , where exp is an isomorphism. Find
, where exp is an isomorphism. Find 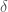 such that
such that  on
on  and such that
and such that  on
on  , where
, where  is the invariant bilinear form gotten by restriction from
is the invariant bilinear form gotten by restriction from  .
.
Then, if I haven't screwed up, and
and  . That deals with the nondominant terms.
. That deals with the nondominant terms.
(continued)
For the dominant terms, you need to bound . We should be able to write
. We should be able to write  , where I may well have the constants wrong. So we need to deal with
, where I may well have the constants wrong. So we need to deal with  .
. and see that your error term is
and see that your error term is  times your main term.
times your main term.
Make the change of coordinates
Approximating integrals of the form , as
, as 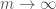 , and where
, and where 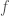 has an isolated simple critical point, is a common task. The approach is always, near that critical point, to write
has an isolated simple critical point, is a common task. The approach is always, near that critical point, to write  , where
, where  is a positive definite quadratic and
is a positive definite quadratic and 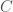 has cubic order. One then makes a linear change of variable to get
has cubic order. One then makes a linear change of variable to get  , where the ellipses is a series that decays with
, where the ellipses is a series that decays with 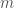 . I thought that Etingof told me this was called the “stationary phase approximation”, but wikipedia seems to think that deals with oscillatory integrals.
. I thought that Etingof told me this was called the “stationary phase approximation”, but wikipedia seems to think that deals with oscillatory integrals.
One bug in the preceeding: at
at  . The easiest fix is probably to use that
. The easiest fix is probably to use that 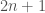 dimensional representation:
dimensional representation:  .
.
The phrase “stationary phase approximation” is sometimes used when “method of steepest descent” is the more appropriate choice.
The easiest argument I have seen about finite-dimensionality for irreducible representations of compact groups is provided by Serge Lang in his book on $SL(2,\mathbf{R})$. It assumes existence of Harr measures and finiteness of volume of $K$, and nothing else.
That is nicely written, thanks! Section II.2, for those who want to look it up.