This is the next in my series of posts on different ways to think about local systems. This time, we will consider an approach where we only build isomorphisms along infinitesimally short paths. If you pursued this line of thought long enough — and thought very hard about finite characteristic issues — you would come to the definition of a crystal. But I don’t plan to go nearly that far; I’ll just give you the intuitions in characteristic zero.
I think this is probably the hardest of the three perspectives I want to explore, but it logically comes second. Things will become a bit easier again when we get to our third perspective, connections.
To try to make this a bit easier, I’ll start with a nonstandard presentation; then reboot and give the actual definitions.
In our last discussion, we took a vector bundle on a space
and, for every path
in
from
to
, we gave an isomorphism
from
to
.
We don’t really need to know the maps for every path
. We only need to know how to deal with short paths, because we can break any long path up into a chain of short paths.
Let’s try to make this notion of “short paths” precise. Let be an open subset of
; intuitively,
will be the set of
such that
is near
. We require that
(1) for every , the diagonal point
is in
.
(2) if and only if
.
(3) for any , the set
is a ball.
For example, if we have a metric on
, we can take
to be
for some sufficiently small
.
Definition B.1: An input of type B.1 consists of a (1) a vector bundle on
and, for every
, an isomorphism
between
and
such that, if
,
and
are all in
, then
.
It will turn out to be worthwhile to rephrase this definition in a way which avoids mentioning the individual points of . Let
.
We have three projections from to
, call them
,
and
. (So
projects onto coordinates
and
and so on.) We have two projections from
to
: call them
and
.
So we can make
Definition B.2 An input of type B.2 is a vector bundle on
, and an isomorphism
of vector bundles on
, such that
.
That formula may look awfully abstract, but if you write it out you’ll see that it simply the formula from definition B.1.
Let’s try to see what looks like in local coordinates. For simplicity, I’ll take
to be one dimensional. Let
and
denote the first and second coordinates on
. So, for
a section of
, instead of writing
and
, I’ll write the more intuitive
and
.
Let be some (local) section of
. We can expand
as a power series
(*)
for some sections of
, each depending on
. Since
has to be trivial on the diagonal, we have to have
. There are many relations between the
‘s, which will come up in later posts.
By the way, if had dimension
, we’d replace
by
. So there is nothing deep there.
Now comes the point that I think a lot of people will find challenging. Above, I worked with an honest open set in
. What we are actually supposed to do is work with a formal neighborhood of the diagonal in
. Intuitively, this means that we work with formal sums like (*). Let’s give a definition along these lines:
Definition B.3 An input of type B.3 is a vector bundle on
, and, on an open cover of
, formal power series like (*), which formally agree on overlaps, formally give linear maps
and formally obey
.
Inputs of type B.1 and B.2 are easily equivalent, but type B.3 is different. We don’t impose that our power series converge, and we identify functions that have the same Taylor series. (Such as and
.) I believe that there is some theorem that we do get equivalent categories in the end, but this isn’t trivial.
In definition B.3, the spaces and
went away. We can get them back, and prettify our definition, by using the notion of the formal neighborhood of the diagonal in
. This requires the toolkit of modern algebraic geometry. Namely, let
denote the sheaf of functions on
. Let
denote the subsheaf of functions vanishing on the diagonal. For every
, there is a closed subscheme
of
, whose underlying topology is the same as
, but where
for any open set
. The formal neighborhood of the diagonal, which I’ll denote by
, is the
inverse direct limit of the . The space
has two maps to
, which we denote
and
. These are both the identity on the underlying topological space, but they pull back functions differently.
Definition B.4 An input of type B.4 is a vector bundle on
, and an isomorphism
of vector bundles on
, such that
.
This is nothing but a repackaging of definition B.3.
There is another mind blowing idea still to come, due to Grothendieck: is the universal infinitesimal thickening of
. What this means is that, given an input of type B.4, a thickening
of
and two maps
and
from
to
, we canonically get an isomorphism between
and
. I think the
-category people will really like this part! But this post is too long, so I’ll save it for another installment.
In the meantime, if you want to prepare for the connection perspective, you might want to think about the following:
Question: We want to be a linear map, so
. What does this tell us about the
‘s? And, similarly, what does the condition
say about the
‘s?
Do you know what happens if you do this with a different Lie algebroid than the tangent bundle, and cook up its own version of the formal neighborhood of the diagonal (it should be dual to the formal group of power series)? This should give a formal ‘connection’ in the sense that moving an infinitesmal amount in a direction given by the Lie algebroid should give an isomorphism on the fibers. Do the corresponding notion of local system and cohomology correspond to anything nice?
There is a functorial way to think of nearby points: We say an S-point is a map from a scheme S to X, and two S-points are “close” if the two maps agree on the reduced subscheme . This leads to an interpretation of
. This leads to an interpretation of 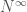 as a left adjoint to killing nilpotents.
as a left adjoint to killing nilpotents.
Also, I think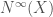 is a direct limit, and it’s usually only representable in a larger category than schemes, like locally ringed spaces.
is a direct limit, and it’s usually only representable in a larger category than schemes, like locally ringed spaces.
Scott: Thanks for the correction. It is indeed a direct limit, not an inverse limit. You are also right that I need locally ringed spaces, not just schemes, to represent it. I’m going to decide that locally ringed spaces are part of “the toolkit of modern algebraic geometry”, so I don’t have to fix that.
The functorial perspective you bring up is interesting. How far can we take it? For example, could I define my input as (1) a vector bundle on
on  and (2) for
and (2) for  any nilpotent thickening of a point and
any nilpotent thickening of a point and  and
and 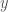 two
two  -valued points of
-valued points of  with the same reduction, an isomorphism between
with the same reduction, an isomorphism between 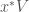 and
and  , obeying certain functorial conditions?
, obeying certain functorial conditions?
Greg: I know of one example like this — the distinction between real and holomorphic connections on a complex manifold. Let be a complex manifold. Let
be a complex manifold. Let 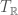 be the tangent bundle to the underlying real manifold;
be the tangent bundle to the underlying real manifold;  the commplexification
the commplexification 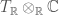 and
and 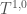 the subbundle of
the subbundle of  consisting of holomorphic vector fields.
consisting of holomorphic vector fields.
Smooth connections on real vector bundles come from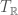 while holomorphic connections come from
while holomorphic connections come from 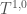 . I’ve been working in algebraic language, which sweeps all of these issues under the rug and starts with
. I’ve been working in algebraic language, which sweeps all of these issues under the rug and starts with 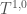 . But I think (don’t quote me!) that a differential geometer would say that
. But I think (don’t quote me!) that a differential geometer would say that 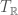 was the tangent bundle, and
was the tangent bundle, and 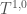 was a Lie algebroid.
was a Lie algebroid.
Some more musing: I see from wikipedia that, when has an action of a group
has an action of a group  , the
, the  -invariant vector fields on
-invariant vector fields on  form a Lie algebroid. Can you get equivariant cohomology in this way?
form a Lie algebroid. Can you get equivariant cohomology in this way?
David,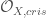 -module.
-module.
I would say that this perspective can be taken very far – you can take families of objects other than vector spaces, and you get nonlinear structures like D-schemes (introduced by Beilinson and Drinfeld). Back to the main point, I think your input works, but I don’t know a proof. (For the benefit of algebraists, “thickening of closed point” is the same as “spectrum of Artinian local ring”.) For some reason, I usually see S-points for S ranging over thickenings of Zariski opens rather than closed points, and the compatibility relations yield the definition of locally free
“For some reason, I usually see S-points for S ranging over thickenings of Zariski opens rather than closed points, and the compatibility relations yield the definition of locally free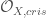 -module. ”
-module. ”
That’s my next post!
Greg: Given any Lie algebroid, one can consider a notion of D-modules for this Lie algebroid. This construction is explained in section A.3 of Frenkel-Ben-Zvi where they concentrate on the example of twisted differential operators.
Also in section A.2 of Frenkel-Ben-Zvi, they discuss the notion of crystalline connections, much as David did in his post. In particular, they give the reformulation that David gives in his comment #3 above. According to F-BZ, the condition on the isomorphisms is extremely simple — just transitivity
is extremely simple — just transitivity 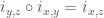 .
.
This crystalline point of view seems extremely similar to D-modules and I guess they agree for smooth varieties in characteristic 0. Will there be a post explaining why they differ in other situations?
Finally, let me just say that this is a great series of posts!
A minor point regarding 2 and 3: the locally ring space N^{\infty} is an example of what is called a formal scheme.
Right, so for a Lie algebroid, you can cook up its (sheaf of) enveloping algebra(s), and then look at to get an cohomology theory that is the same as the deRham cohomology if you take the tangent Lie algebroid. If you start with a Lie group action, and take the associated infinitesmal action Lie algebroid, I believe you get something very close to the equivariant cohomology. In particular, I think its what happens if you try to use the Weyl model to compute equivariant cohomology, and neglect to take invariants under the action of the group, and instead only take the horizontal subcomplex.
to get an cohomology theory that is the same as the deRham cohomology if you take the tangent Lie algebroid. If you start with a Lie group action, and take the associated infinitesmal action Lie algebroid, I believe you get something very close to the equivariant cohomology. In particular, I think its what happens if you try to use the Weyl model to compute equivariant cohomology, and neglect to take invariants under the action of the group, and instead only take the horizontal subcomplex.
I guess I was looking for a crystalline version of this picture, and I think Joel pointed me in the right direction for this.
Also, I’ll second Matthew’s minor point, but not because I love nitpicking. Its worth noting to anyone who hasn’t played with formal schemes before that they correspond to the Spec of topological rings, and that the maps between them must correspond to continuous ring maps. Otherwise, you’ll start contemplating truly ugly objects, like the group of algebra automorphisms of![\mathbb{C}[[x]]](https://s0.wp.com/latex.php?latex=%5Cmathbb%7BC%7D%5B%5Bx%5D%5D&bg=ffffff&fg=444444&s=0&c=20201002) , which is some uncountable product of copies of
, which is some uncountable product of copies of ![\mathbb{C}[[x]]](https://s0.wp.com/latex.php?latex=%5Cmathbb%7BC%7D%5B%5Bx%5D%5D&bg=ffffff&fg=444444&s=0&c=20201002) (since it is uncountably generated as an algebra).
(since it is uncountably generated as an algebra).
Incidentally, is anyone else disappointed by Hartshorne’s treatment of formal schemes? EGA1 actually bothers to define things like Spf (French for “formal spectrum”).