When confusions annihilate

As mathematicians we spend most of our lives confused about something or other. Of course, this is occasionally interrupted by moments of clarity that make it worth it. I wanted to discuss a particularly pleasant circumstance: when two confusions annihilate each other. I’ll give two examples of times that this happened to me, but people are encouraged to provide similar examples in the comments.

In both cases what happened was that I had:

• A question to which I didn’t know the answer
• An answer to which I didn’t know the question

Artin-Wedderburn in fusion categories

In quantum algebra we’re often studying some classical algebraic notion, but instead of working in the category of vector spaces you instead work in a more general tensor category. For example, the theory of finite type knot invariants is roughly the theory of simple Lie algebra objects in symmetric tensor categories, while the theory of subfactors is roughly that of simple algebra objects in unitary tensor categories. The basic question is then which notions from the classical theory generalize to the quantum setting. For example, is there an analogue of Artin-Wedderburn for semisimple algebra objects in fusion categories? The goal of this post is to argue that the following theorem (due to Ostrik, modulo any errors I’ve introduced) gives a satisfactory generalization.

Any semisimple algebra object in a fusion category is isomorphic (as an algebra object) to the internal endomorphisms End(X) for some object X in a semisimple module category over .

First I’ll unpack the definitions in this statement and then I’ll explain how Artin-Wedderburn for semisimple algebras over a fixed field k follows from this statement. I’ve been thinking about this theorem because Pinhas Grossman and I have been using it to classify “quantum subgroups” of the Haagerup fusion categories, but that’s a story for another day.

The decline of quantum algebra (QA)

I was browsing through different category listings on the arXiv today and noting the changes in numbers of papers over the years. As you might expect, there are more and more papers being posted to the arXiv every year. However, one category defies this trends: QA (quantum algebra).

There are actually less papers being posted to QA in the past three years (2010 317, 2009 308, 2008 323), than there were in the late 90s (1998 364, 1997 434, 1996 395). By contrast, there are about 4 times as many AG papers in the past few years compared to the late 90s, about 10 times as many RT papers, and about 5 times as many GT papers.

What do you make of this? Does it represent a trend in the kind of math that people are doing? Or are people just classifying their work differently?

It would be interesting to see if one can use this arXiv category to get a sense of which fields are becoming more and less popular over time.

The Brauer Groupoid

Recall that the Brauer group of a field k consists of central simple algebras over k up to Morita equivalence with the group operation given by tensor product. For example, the Brauer group of the real numbers is Z/2 because the only central simple algebras are matrix algebras over or matrix algebras over the quaternions , and . It is a well-known and fundamental fact that the Brauer group is isomorphic to the second Galois cohomology where is the seperable closure of k.

What I’d like to explain in this post is a follow-your-nose proof of this isomorphism which comes from thinking about fusion categories. Namely, attached to any fusion category there is a very natural object called Brauer-Picard groupoid (introduced by Etingof-Nikshych-Ostrik). For the special case of the fusion category of vector spaces over k the Brauer-Picard groupoid has a point for every seperable extension of k and the group of automorphisms of the point k gives exactly the Brauer group. However, one can also look at the group of automorphisms of other points, in particular the point . The group of automorphisms of that point is instead naturally isomorphic to the Galois cohomology . Since the groupoid is connected we see that the Brauer group coincides with the Galois cohomology. In fact, there’s a natural choice of arrow from to and so a natural choice of isomorphism between the two groups.

This example came up in work in progress with Pinhas Grossman where we compute the Brauer-Picard groupoid of the fusion categories which come from the Haagerup subfactor. As we’ll see the automorphism group of a point in the Brauer-Picard groupoid has a subgroup consisting of certain “outer automorphisms.” I wanted to have a good example in hand where the outer automorphism group of different points were different in order to test certain lemmas. The example in this post is as extreme as things can get, for there are no nontrivial outer automorphisms, while for the whole group consists of outer automorphisms.

Cyclotomic integers, fusion categories, and subfactors (March)

Frank Calegari, Scott Morrison, and I recently uploaded to the arxiv our paper Cyclotomic integers, fusion categories, and subfactors. In this paper we give two applications of cyclotomic number theory to quantum algebra.

1. A complete list of possible Frobenius-Perron dimensions in the interval (2, 76/33) for an object in a fusion category.
2. Given a family of graphs G_n obtained from a graph G by attaching a chain of n edges to a chosen vertex, an effective bound on the greatest n so that G_n can be the principal graph of a subfactor.

Neither of these results look like they involve number theory. The connection comes from a result of Etingof, Nikshych, and Ostrik which says that the dimension of every object in a fusion category is a cyclotomic integer.

A possible subtitle to this paper is

What’s so special about ?

Knot polynomial identities and quantum group coincidences (February)

Scott Morrison, Emily Peters and I have just uploaded to the arxiv our paper Knot polynomial identities and quantum group coincidences. In this paper we prove several new strange identities between certain specializations of colored Jones polynomials and other classical knot polynomials. For example, we prove that for any knot (but not for links!) the 6th colored Jones polynomial at a 28th root of unity is twice the value of a certain specialization of the HOMFLYPT polynomial (for the exact formulas see the first page of the paper).

Each of these identities of knot polynomials comes from a coincidence of small tensor categories involving the even part of one of the 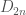subfactors. For example, the above identity comes from an equivalence

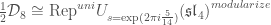
To recover the knot polynomial identity, one computes the Reshetikhin-Turaev invariant for a particular object on the left (getting half the relevant colored Jones polynomial for knots, but something worse for links) and for the corresponding object on the right (getting the specialization of HOMFLYPT).

(In that equation above there’s a lot of technical terms on the right side. “Uni” means we’re using Turaev’s unimodal pivotal structure instead of the usual pivotal structure, and “modularize” means take the Bruguieres-Mueger modularization where you add isomorphisms between the trivial object and all simple objects that “behave like the trivial object.”)

For most of these coincidences we give no fewer than three separate proofs, as well as an exciting diagram which explains the proof in pictures. After the jump I’ll sketch the flavor of these different arguments.

One of the biggest difficulties in writing this paper was getting all our conventions straight because we constantly need to jump between different quantum groups, and knot polynomials. Life becomes very messy if you’re using one convention for q in one place and a different one somewhere else. So one goal of this paper is to be “full of correctness.” We hope that if you ever wanted to know about the relationship between quantum groups and diagramatics you can just look at this paper and have nice consistent conventions for everything. In particular, if you notice even small errors we’d really love to hear about them so that they can be fixed.

TQFTs via Planar Algebras (Part 3)

This is the third and final post in my series about using planar algebras to construct TQFTs. In the first post we looked at the 2D case and came up with a master strategy for constructing TQFTs. In the last post we began carrying out that strategy in the 3-dimensional setting, but ran into some difficulties. In this post we will overcome those difficulties and build a TQFT.

Bleg: testing algebraic integrality by computer.

Update 2: we’ve found a nice answer to our question. Maybe it will appear in the comments soon. –Scott M

Scott, Emily, and I have an ongoing project optimistically called “The Atlas of subfactors.” In the long run we’re hoping to have a site like Dror Bar-Natan and Scott’s Knot atlas with information about subfactors of small index and small fusion categories. In the short run we’re trying to automate known tests for eliminating possible fusion graphs for subfactors.

Right now we’re running into a computational bottleneck: given a number that is a ratio of two algebraic integers how can you quickly test whether it is an algebraic integer? Mathematica’s function AlgebraicIntegerQ is horribly slow, and we’re not sure if that’s because it’s poorly implemented or whether the problem is difficult. So, anyone have a good suggestion? After the jump I’ll explain what this question has to do with tensor categories (and hence subfactors which correspond to bi-oidal categories as I’ve discussed before).

To whet your appetite, here’s an example. Is , where

and where is the largest real root of

an algebraic integer? Mathematica running on Scott’s computer (using the builtin function AlgebraicIntegerQ) takes more than 5 minutes to decide that it is.

Update: Thanks to David Savitt for pointing out that both this example and an earlier one are answered instantly by MAGMA. Blegging is already working. But what’s the trick? Is it something we can teach Mathematica quickly? –Scott M

Group rings arrr commutative

If you are familiar with group rings, you might think that the title of this post is false. If G is a nonabelian group, multiplying the basis elements g and h in can yield , so we have a problem. In general, if you have a problem that you can’t solve, you should cheat and change it to a solvable one (According to my advisor, this strategy is due to Alexander the Great). Today, we will change the definition of commutative to make things work.

Reference Hunt I

Does anyone know where the following useful facts were first proved? A lot of papers just say, "It is known that…" and I’d like to give proper attribution in some future work.

Let A be an abelian group, and let denote the monoidal category of A-graded complex vector spaces. Then:

1. Equivalence classes of braided structures on are classified by elements of .
2. also classifies -valued quadratic forms on A.
3. , where the right side is "Eilenberg-MacLane abelian group cohomology" (defined in MacLane’s 1950 ICM address).

There is an additional neat interpretation involving double loop maps and multiplicative torsors on A, but I don’t need that level of sophistication for the near future.