Reference Hunt I

Does anyone know where the following useful facts were first proved? A lot of papers just say, "It is known that…" and I’d like to give proper attribution in some future work.

Let A be an abelian group, and let Vect^A denote the monoidal category of A-graded complex vector spaces. Then:

  1. Equivalence classes of braided structures on Vect^A are classified by elements of H^4(K(A,2),\mathbb{C}^\times).
  2. H^4(K(A,2),\mathbb{C}^\times) also classifies \mathbb{C}^\times-valued quadratic forms on A.
  3. H^4(K(A,2),\mathbb{C}^\times) = H^3_{ab}(A, \mathbb{C}^\times), where the right side is "Eilenberg-MacLane abelian group cohomology" (defined in MacLane’s 1950 ICM address).

There is an additional neat interpretation involving double loop maps and multiplicative torsors on A, but I don’t need that level of sophistication for the near future.

9 thoughts on “Reference Hunt I”

  1. Hey Scott, you lucked out. It just so happens I’ve been thinking about the same sort of things.

    So Part 3 is in Eilenberg and MacLane’s series of 1950 papers: “On The Groups H(pi, n) I, II, III. These papers give me a little headache reading because this was all done before simplicial sets were around. They spend a lot of time explaining what a “FD-complex” is which is really just a simplicial set. Their construction is basically an iterated version of the bar resolution, but applied to simplicial abelian groups (you get bisimplicial sets and take the diagonal). I think nowadays this also goes under the name “W-construction”.

    Part 2 follows immediately from the Whitehead exact sequence and universal coefficients. This goes back to Whiteheads 1950 paper: “A Certain Exact Sequence”. This is a long exact sequence which in this case splits as:

    0 = \pi_4\to H_4 \to \Gamma_3(A) \to \pi_3= 0

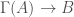
    Here \Gamma_3(A) = \Gamma(A) is Whitehead’s Gamma functor. It takes an Abelian group and constructs the universal quadratic form for it, i.e. \Gamma(A) is a group which satisfies the following universal property: linear maps \Gamma(A) \to B
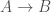    are the same as quadratic maps A \to B. Whitehead gives an explicit construction of generators and relations for \Gamma(A) in terms of the elements of A. Once you have this isomorphism, you need to use universal coefficients to show,

    H^4(K(A,2), \mathbb{C}^\times) = hom( \Gamma(A), \mathbb{C}^\times)

    This follows because H_3(K(A,2) = 0. Why is it zero you ask? Well you probably remember the Hurewicz map:

    h: \pi_k \to H_k

    (for simply connected spaces) this is an isomorphism for the first non-trivial group, but it is still surjective for the next group. In this case \pi_3 = 0, so H_3 = 0.

    Part 1 is more tricky. I don’t know a reference, but here is a proof. First you need a lemma which says that the braided monoidal structures on Vect^A are determined by their restriction to the A-graded lines. I doubt this lemma is true as stated. What you need is a condition which says the monoidal structure is compatible with the direct sum in the obvious way. Once you have this, I believe that you could reduce to the case of lines, since every A-graded vector space is a direct sum of A-graded lines. You still have to be careful that when you tensor two A-graded lines together, you get an A-graded line. I guess since you are fixing the monoidal structure at the beginning this isn’t such an issue.

    So this reduces the problem to finding the braidings on the subcategory of A-graded lines. There is no problem just using invertible morphisms. So what you are dealing with is a picard groupoid (the monoidal groupoid of A-graded lines) (aka a weak 2-group) and you’re asking what are the braidings on this? There are several ways to precede at this point.

    One way is see that the associator and pentagon identity really just give you a cocycle in H^3(A; \mathbb{C}^\times), plus a braiding which is a map A \otimes A \to \mathbb{C}^\times which satisfies some conditions. If you look hard at Eilenberg and MacLane’s papers you see that their cocycles for H^3_{ab} are exactly the same data (mod coboundaries).

    Another approach is to use the equivalence between braided 2-groupoids and spaces with only non-trivial \pi_2 =A and \pi_3 = \mathbb{C}^\times. If you fix the homotopy groups a little obstruction theory shows these are classified by an element in H^4(K(A,2), \mathbb{C}^\times). This element is called the k-invariant.

  2. I should point out that the k-invariant in H^4(K(A,2), \mathbb{C}^\times) doesn’t really classify braidings. What it really classifies are the combination of an associator together with a compatible braiding. If you’re just interested in the braidings compatible with a fixed associator a, you’re going to have to look at the fiber over a of the map,

    H^4(K(A,2) ; \mathbb{C}^\times) \to H^3(A; \mathbb{C}^\times)

  3. Thanks, Chris. That was really helpful.

    I’m pretty sure H^4(K(A,2), \mathbb{C}^\times) is what I want, because I’m looking for equivalence classes of braided category structures, rather than explicit braidings. As far as I can tell, two maps A \otimes A \to \mathbb{C}^\times from the Eilenberg-MacLane data produce equivalent braided categories if they yield the same quadratic form on A.

    Here’s a sketchy homotopy theoretic justification: A braided tensor structure on Vect^A is the same as a double loop map A \to K(\mathbb{Z},3), since the target space classifies categories (or slightly more rigorously, Vect-bundles), and double loop maps are precisely those that preserve E_2 structure. Delooping twice, we want homotopy classes of maps K(A,2) \to K(\mathbb{Z},5).

  4. Glad I could help. Right. what I meant was that H^4(K(A,2); \mathbb{C}^\times) classifies equivalence classes of pairs: associator + compatible braiding.

    More precisely, Eilenberg and MacLane’s so called abelian group cohomology cycles consist of exactly this data: a specific 3-cocycle (the associator) and a specific map b:A \otimes A \to \mathbb{C}^\times. The counboundaries take care of when two such things give equivalent braided monoidal structures. In this sense H^4(K(A,2); \mathbb{C}^\times) classifies equivalence classes of pairs of data.

    In terms of this data the map to hom(\Gamma(A), \mathbb{C}^\times) is given as follows. By the universal property such a homomorphism is the same as a quadratic map A \to \mathbb{C}^\times. From the above cocycle data we get such a map by a \mapsto b(a,a). The amazing thing is that this association is an isomorphism,

    H^4(K(A,2); \mathbb{C}^\times) \cong hom(\Gamma(A), \mathbb{C}^\times)

    So yes you are basically correct. Two braidings are equivalent when they produce the same quadratic map A \to \mathbb{C}^\times. My point is that if you choose a quadratic map and a map A \otimes A \to \mathbb{C}^\times which induces the quadratic map, it might not come from a braiding. And even if it does come from a braiding it might need some strange associator which you don’t want.

    (Also I was thinking \mathbb{C}^\times as a discrete group. You have to be a little careful if you want to translate this to \mathbb{Z}-cohomolgy. Is there a topology on A?).

  5. Chris,

    I don’t see where discreteness of \mathbb{C}^\times is necessary here. If we’re taking cohomology with coefficients in a constant sheaf, the topology of the fiber is irrelevant (unless you want to do further manipulations on the cohomology groups later on).

    My abelian group A is actually finite and rather small, but I phrased the question in more generality, because I figured someone who lived and breathed U_q(\mathfrak{g}) would know about this stuff. I guess it didn’t matter, since you answered most of the question.

  6. The discreteness of C* is relevant to passing between cohomology with Z coefficients and C* coefficients. The exponential sequence Z -> C -> C* gives you a boundary map comparing them, but it isn’t an isomorphism unless you can make cohomology with C coefficients go away. If you have a finite group, it certainly does. But not in general, which suggests that you might want some modification to C* to make K(Z,5)=B^5(Z)=B^4(C*).

    Also, there’s the question of what you really want, although it’s probably not clear, since your group is finite. If you use discrete C* coefficients, you probably get precisely what you originally asked for, whereas, if you use continuous C* coefficients, you probably get a braided monoidal homotopy theory, suited to vector bundles, but not an honest category. In your argument identifying K(Z,3) as a classifying space for Vect-bundles, they are bundles of categories like the category of vector bundles, not the category of local systems.

    I would not say that “If we’re taking cohomology with coefficients in a constant sheaf, the topology of the fiber is irrelevant,” but rather that constant coefficents means discrete topology on the fibers. Instead you could use the sheaf of continuous functions to your topological group. This does not change the Z part, but the sheaf of functions to C is now fine so it has no higher cohomology, so the boundary map is an isomorphism.
    I would rather work with sheaves with values in topological abelian groups (or chain complexes), up to homotopy equivalence. That way, the global continuous functions to C or C* are small homotopy types rather than big sets, but this won’t change anything else.

    Anyhow, this modification gives you an isomorphism between cohomology with Z coefficients and shifted cohomology with continuous C* coefficients, but it no longer matches the discrete quadratic form picture. Universal coefficients says that quadratic forms with values in Q/Z still show up (and the roots of unity was the only part of C* that mattered in the old version), but now there’s an extra part, the dual of the fifth homology of the Eilenberg-MacLane space.

  8. My understanding which I learnt from John Baez is that 1 – the result about equivalence classes of braidings on Vect^A – came up in Joyal and Street’s original paper (not the published version)… though I’m not sure if this was the first time it was treated:

    André Joyal and Ross Street, Braided monoidal categories,
    Macquarie Mathematics Report No. 860081, November 1986. Pdf link.

    See this discussion at the n-category cafe.

  9. Thanks Bruce. Now all of my questions have been answered. This has been a very satisfying blog experience.

Comments are closed.