Poncelet’s Porism

One of my hobbies is collecting examples of theorems which are geometry in the sense that Euclid would understand the term, yet illustrate ideas of modern algebraic geometry. I’m going to start posting explanations of some of these results here. My first example is a nineteenth century result known as Poncelet’s Porism.

Poncelet’s Porism
Let C and D be two conics. Carry out the following process. Take a point p_0 on C. Draw a tangent to D through p_0, and let p_1 be the other point where this tangent meets C. Now, draw the other tangent to D passing through p_1 and let p_2 be the point, other than p_1, where this tangent line meets C. Continuing in this fashion, define p_3, p_4 and so forth. Now, suppose that p_N=p_0. In that case, if we had started the process at some other point p'_0 on C, and defined p'_0, p'_1, p'_2 in the same manner, then we would also have p'_N=p'_0.

Here is an excellent animated picture, from Mathworld, of the points p_i sliding around as we move p_0.

Image of Poncelet's porism

From a modern perspective, Poncelet’s Porism is interesting because it is one of the few theorems of classical geometry which involves a non-rational variety — namely a genus one curve.

One of the basic tools of modern algebraic geometry is to set up incidence varieties which describe how various figures relate to each other. In this case, let X be the space of pairs (p, \ell) so that the point p is contained in the line \ell, the point p is contained in C and the line \ell is tangent to D. (One of the great things about the modern approach is that I can talk about this object without discussing what projective space it lives in.) Let \sigma be the involution of X which sends (p, \ell) to (p', \ell) where p' is the other point, besides p, where \ell meets C. Similarly, let \tau be the involution sending (p, \ell) to (p, \ell') where \ell' is the other tangent, besides \ell, to D passing through p. Our geometric construction is just repeatedly alternating between \sigma and \tau. What we want to show is that, if (\sigma \tau)^N has a fixed point, then (\sigma \tau)^N must be the identity.

In differential geometry, X is simply a disjoint union of two circles (if the conics are nested), and there is no reason that (\sigma \tau)^N might not have some complicated collection of fixed points. However, in algebraic geometry, we get to see these two circles as the real points of a complex curve, and the complex geometry of this curve is much more restrictive. So, let us now think about the construction of X with complex coordinates instead of real ones and ask what kind of curve X is. Let D^* denote the dual conic to D, that is, the space of lines tangent to D. Then, by definition, X embeds into C \times D^*. Recall that a conic is a genus zero curve, which we might as well think of as \mathbb{C} \mathbb{P}^1, so X embeds into \mathbb{C} \mathbb{P}^1 \times \mathbb{C} \mathbb{P}^1.

Next, check that X is smooth. This is trickier than it seems, because once we move to looking at complex points, there are four points of X where projection onto C does not give a local coordinate. Namely, at the preimages of the four intersection points of C and D. Similarly, there are four points at which projection onto D^* does not give a local coordinate. (Can you see what they are? Hint: draw the two conics to meet at four real points and the picture will be easier to visualize.) When the conics are drawn in a nested configuration, these eight bad points on X have complex coordinates, so it is easy to ignore them, but they do affect the geometry. In any case, it turns out that, at every point of X, either projection to C or projection to D^* gives a local coordinate, so X is smooth.

Now, over a generic point of C, there are two points of X. And, over a generic point of D^*, there are also two points of X. So X is a smooth hypersurface in \mathbb{C} \mathbb{P}^1 \times \mathbb{C} \mathbb{P}^1 of degree (2,2). Here’s an exercise for those who’ve just taken an algebraic geometry course: check that X is a curve of genus one. Here is a harder exercise: obtain the same result by embedding X into the flag variety of pairs (p,\ell).

Now, a genus one curve is topologically a torus S^1 \times S^1. If we pick a point on X to call the origin, then it naturally acquires an abelian group law, where the group is also S^1 \times S^1. In terms of this group law, every involution of X is of the form x \mapsto y-x for some y \in x. So, \sigma(x)=y-x for some y and \tau(x)=z-x for some z. We compute that (\sigma \tau)(x)=(y-z)+x. In other words, \sigma \tau is a translation on X. So (\sigma \tau)^N is also a translation on this group. In any group G, if translation by g has a fixed point, then g is the identity element and every point is fixed under translation by G. This was the desired conclusion. QED

Two final notes. First, choosing a base point to call zero on X was unnecessary. The morally correct argument proceeds in terms of principal homogenous spaces. Exercise: give this argument.

Second, there is a very interesting classical problem posed by Poncelet’s porism when the two conics are circles. Let the radii of the circles be R and r, and the distance between their centers be d. Give conditions, in terms of R, r and d, for when the construction cycles with period N. One of the nifty things that we get almost for free from modern algebraic geometry is that this relation will be given by a polynmial. For N=3, the explicit polynomial is d^2 =R^2 - 2 Rr; this formula was found by Euler and is proven here. The formulas grow more and more complex as N grows; Mathworld has a list for N up to 20, with some gaps. I notice that the formula for N=11 was much harder to find than those for 4, 5, 6, 7, 8, 9, 10, 12, 14, 16, 18 and 20. The modular curve X_0(11), which parameterizes genus one curves with a translation by a point of order 11, is not rational, whereas the modular curves for all of these other values of N are. (I am cheating a bit in my description of X_0(11).) This is surely not a coincidence…

16 thoughts on “Poncelet’s Porism”

  2. Wow! I’ve been looking for an explanation of this since I started gradschool. Thanks David.

  3. David,

    That was a lot of fun to read. I’m looking forward to the next one.

    You didn’t leave me with any unanswered questions, so instead let me add this: The wikipedia page on Porism does not in fact answer the question of what the term “porism” means, but it’s interesting reading anyways.

  4. I saw a talk by Hitchin in 1994 relating this result to finding algebraic solutions to Painleve VI (which has mostly transcendental solutions). Hitchin had some crazy slides, one being a discussion of this problem in an American math journal from, if I recall, the 18th century. At the time, all the figures were collected at the end of the journal. (Another slide was a political cartoon skewering Painleve!)

  5. That’s a really nice post (and I’ve never seen this theorem before – or at least I don’t remember…). I hope you will continue with a series along these lines!

  7. Gavin — that’s a really nice question that I don’t know the answer to. Another way to put the problem is that, given two points (p,l) and (r,n), we want to construct the image of (q,m) under the involution that swaps (p,l) and (r,n). Does anyone have an idea what that involution ought to be?

  8. David – I think you have given me the key. Let l and n touch D at s and t. Let P be the intersection of the line joining p and r with the line joining s and t. Then P can be chosen as a focus of involution on C and D. The involution takes (q,m) to (q’,m’) where the line from q to P meets S again at q’ and where m’ is the tangent to D at the point where the line from P to the point of contact of D with m meets D again.
    This has to be the right construction, but there is the little matter of demonstrating that q’ lies on m’. I could probably have done all this in seconds when I was in my teens (Roseveare was our maths teacher’s name) but I have forgotten it all now. We used to cook up projective methods for proving trivialities of Euclidean geometry – a sort of joke to squash peanuts with a sledgehammer. But this was back in the early 50s.

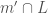  9. Gavin — Your solution feels wrong to me because it doesn’t respect the self dual nature of the picture. Your recipe for constructing q’ (which I like) is to take the other point in C \cap qP for some fixed point P. This suggests to me that m’ should be the other tangent to D from m' \cap L for some fixed L.

    As you say, though, the real test is to determine whether or not q’ lies on m’.

  10. Actually, neither your solution nor my modification can be right. There is an irritating reason for this, which I thought of when I first thought about this question a few weeks ago and then forgot. Let i be the involution we are trying to compute, and let p be the projection from the elliptic curve X to the conic C. Then p(x) does not determine p(i(x)). So any rule which builds q’ by looking only at q and not at m has to be wrong.

  11. Yes, my failing attempts to show that q’ lies on m’ had damped my belief in the construction.
    There are so many objects generated by the pair (C,D). I need to get a tighter grip on the symmetries of the situation, to rule out the dross.

  12. Here is another go. I came across interesting communications between David Madore and Ilya Zakharevich which might be relevant. They show that the 4 points of intersection of C and D have the same cross-ratio on C as the 4 common tangents of C and D on D.
    Choose (x1,y1),(x2,y2) on X. Let E be the conic through the 4 points of intersection of C and D and [y1y2]. Let y0 be its tangent at [y1y2]. Let F be the conic inscribed by the 4 common tangents of C and D and [x1x2], and let x0 be its point of contact with [x1x2]. Now consider involution on C through x0 and involution on D along y0. So if (a,b) is a point of X let a’ be the _other_ intersection of [ax0] with C and let b’ be the _other_ tangent to D from [by0].
    Does the fact quoted about cross-ratios tell us that a’ lies on b’?
    I am trying to get my head round my scrappy diagrams. Help, somebody!

  14. A very simple indeed proof of Poncelet’s porism is to be found in:
    AMS’ Mathematical World volume 20:
    Ueno, Shiga, Morita:
    A mathematical gift II, pp. 117-127

Comments are closed.