The meaning of knot homology

What I left out of my post on knot homology was, perhaps, the elevator pitch (if you’re in an elevator with a mathematician who already has some background). I’m giving a talk tomorrow which should include this stuff, and so one possibility is to just drop the slides for that on you, and let that speak for itself. Especially recommended are slides 12 and those past 18 (the rest is more standard quantum topology and categorification stuff).

But I’m not so sure that’s a wise plan. So let me try to say something more bloggy:

A hunka hunka burnin’ knot homology

One of the conundra of mathematics in the age of the internet is when to start talking about your results. Do you wait until a convenient chance to talk at a conference? Wait until the paper is ready to be submitted to the arXiv (not to mention the question of when things are ready for the arXiv)? Until your paper is accepted? Or just until you’re confident you’ve disposed of any major errors in your proofs?

This line is particularly hard to walk when you think the result in question is very exciting. On one hand, obviously you are excited yourself, and want to tell people your exciting results (not to mention any worries you might have about being scooped); on the other, the embarrassment of making a mistake is roughly proportional to the attention that a result will grab.

At the moment, as you may have guessed, this is not just theoretical musing on my part. Rather, I’ve been working on-and-off for the last year, but most intensely over the last couple of months, on a paper which I think will be rather exciting (of course, I could be wrong).

Man and machine thinking about SPC4

I’ve just uploaded a paper to the arXiv, Man and machine thinking about the smooth 4-dimensional Poincaré conjecture, joint with Michael Freedman, Robert Gompf, and Kevin Walker.

The smooth 4-dimensional Poincaré conjecture (SPC4) is the “last man standing in geometric topology”: the last open problem immediately recognizable to a topologist from the 1950s. It says, of course:

A smooth four dimensional manifold homeomorphic to the 4-sphere is actually diffeomorphic to it, .

We try to have it both ways in this paper, hoping to both prove and disprove the conjecture! Unsuprisingly we’re not particularly successful in either direction, but we think there are some interesting things to say regardless. When I say we “hope to prove the conjecture”, really I mean that we suggest a conjecture equivalent to SPC4, but perhaps friendlier looking to 3-manifold topologists. When I say we “hope to disprove the conjecture”, really I mean that we explain an potential computable obstruction, which might suffice to establish a counterexample. We also get to draw some amazingly complicated links:

New Journal: Quantum Topology

The European Math Society Publishing House (a non-profit publishing company which also publishes the Journal of the EMS, CMH, and half a dozen other journals) just announced a new journal: Quantum Topology. I think this is very exciting as it fills a nice hole in the existing journal options. The list of main topics include knot polynomials, TQFT, fusion categories, categorification, and subfactors. So there should be lots of material of interest to people here.

More slides

My tendency to write slideshows instead of actual posts continues. If you like to see oodles of subtle variations on the same talk, you can see my slides from speaking at ARTIN in Glasgow (which just happened to be coincidentally scheduled during the breaks of the categorification conference there), which is the 8th time I’ve given that talk this year (I’m giving a talk today which will be my 13th total talk of 2009. You can see why I’ve been spending more time with Beamer than on the blog).

However, if you’re looking for something newer, this time you have a chance to see the slideshow before the people coming to the talk. I’m speaking on my work with Geordie in about 45 minutes, and made a Beamer show to accompany part of the talk.

Notably, this is the first Beamer I’ve made with Tikz. I’m particularly proud of the picture on slide 17, which I’ve posted under the cut:

Interpreting the Hecke Algebra II: the sheafification

A while back, David wrote a post describing how to produce the Hecke algebra, and I described in comments (very tersely) how David’s description can be categorified. I thought I would expand on that a bit for selfish reasons that will soon become apparent. Not only is some beautiful geometry involved, there’s also a bonus connection to knot homology.

Symplectic duality slides

I’ve been too lazy to write in detail about the progress in my research (well, I am writing six papers and applying to jobs, so it isn’t entirely due to laziness), but I did recently speak in the symplectic seminar at MIT, and have posted the slides on my webpage. Obviously, they’re less useful without someone to explain them, but given the current lack of an overarching paper on the subject (that’s no. 5 on the list, I promise), I thought it might be edifying. Executive summary below the cut.

Hot’n’fresh from the arXiv: 2-block Springer fibers

So, in my first paper based on a blog post (well, loosely adapted), Catharina Stroppel and I have finally posted our paper on 2-block Springer fibers. It was longer in coming than I had expected, but I’m certainly glad that it’s up there now.

Kronheimer on “Knot Groups and Lie Groups”

So, I’m in lovely Edinburgh, Scotland (everyone I’ve told about this said “Scotland? In November?” but it’s not actually worse than New Jersey) in advance of the Maxwell Colloquium on Knot Homology.

By sheer luck, my trip here happened to overlap with the University of Edinburgh’s Whittaker Lecture which is a bit like the Bowen Lectures at Berkeley, except that there’s only one of them. By even more luck, the speaker with Prof. Peter Kronheimer (from Harvard) and the topic was “Knot Groups and Lie Groups.”

Components of Springer fibers, category O, and Khovanov’s “functor valued invariant of tangles”

I’ll just note at the beginning, this post is a bit of an experiment. At this point, it is about a semi-finished research thought of mine (which I’m not 100% sure is original, but I’m putting it out on the internet at least in part hoping that the internet will be able to tell me whether it’s original or not), and will consequently probably be a bit more technical than the average post on this blog, but hopefully, at least a few of you will be able to follow me.

As many of you know, my co-blogger Joel recently posted a preprint (with Sabin Cautis), which constructs a knot homology theory using the geometry of coherent s heaves and Fourier-Mukai transforms on convolutions of minuscule orbits in the affine Grasmannian of .

On the other hand, last year, Catharina Stroppel published a couple of papers on the relationship between Khovanov’s original construction of “a functor valued invariant of tangles” and various flavors of category O. From what I understand, underlying this is a philosophy that the version of Khovanov-Rozansky will be related a block to category O that lies on a dimension 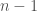-dimensional wall of the Weyl chamber of (where 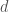is a number relating to the number of strands in your tangle diagram).

One natural question leaps to mind: how are these related?