Last Friday, we had a seminar at Berkeley — or rather, at Noah’s house — featuring Mike Freedman and some quantity of beer. Mike spoke about some of the hurdles he had to overcome in writing his recent paper with Danny Calegari and Kevin Walker. One of the main results of this paper is that there is a “complexity function” c, which maps from the set of closed 3-manifolds to an ordered set, and that this function satisfies the “topological” Cauchy-Schwarz inequality.
Here, 
and 
are 3-manifolds with boundary 
. [EDIT: and equality is only achieved if 
] This inequality looks like the sort of things you might derive from topological field theory, using the fact that 
. Unfortunately, it’s difficult to actually derive this sort of theorem from any well-understood TQFT, thanks to an old theorem of Vafa’s, which states roughly, that there’s always two 3-manifolds related by a Dehn twist that a given rational TQFT can’t distinguish. Mike speculated that non-rational TQFT might be able to do the trick, but what he and his collaborators actually did was an end run around the TQFT problem. They simply proved that that the function 
exists.
I tell you all this, not because I’m about to explain what is, but to explain our new banner picture. We realized after the talk that there were a fair number of us Secret Blogging Seminarians in one place, and that we ought to take a photo.
Secret Blogging Seminar 
What, no one’s GIMPing in the zombie face?
I usually interpret theorems like Vafa’s as a statement that the definition of TQFT could or should be refined, i.e., one may want the target category to have more structure than just Hilbert spaces. I don’t actually have a candidate replacement in mind, although some of the structures in Beilinson’s topological algebras paper look very appealing.
The function c reminds me of some of the pathological counterexamples I saw in a decision theory class I took as an undergraduate. Apparently, some economists really like nonseparable preference systems, but I was never convinced that they were useful for whatever it is that economists do.
Perhaps you could identify the people in the photograph? I’m going to guess Noah Snyder at the far left, then A.J. Tolland, and from there on I’m even less sure.
Actually, Noah is the one
with the big bald spotin the middle with the fleece. Joel is the one in the long pink shirt, A. J. in the hat, David in the middle with the green shirt, and Emily Peters (a friend of the blog) on the far right.So Noah keeps a whiteboard in his yard for just such occasions? You seminarians are certainly dedicated to your trade.
Having been to the talk, I have a question.
What is a rational TQFT? Does it mean that on 2-manifolds the TQFT takes values in Q-vector spaces?
I like the question next to Noah’s head. Is there some interesting context, or possibly an answer?
The short answer was it depends. Sometimes 2-spheres are good and sometimes they’re bad.
Joel,
By a rational TQFT I mean one constructed from a rational 2d CFT, which you should think of as more or less the same thing as a modular tensor category. I’m not sure that this is standard terminology: A “rational TQFT” is really just what mathematicians call a TQFT. The idea is that there should be some more general thing that deserves to be called a TQFT.
My recollection of what Mike said was that Vafa’s result only held when your modular tensor category was semisimple.
I know people address 3dTFTs coming from modular tensor categories by the names of their discoverers: Reshitikhin-Turaev. “Consider the Reshitikhin-Turaev 3d TQFT functor defined by the modular tensor category C…”. I can’t quite recall people saying “rational” for these, even though of course one important point is that these RT-3d TQFT functors allow you to describe rational 2d CFT — if we agree that modular tensor category means: finitely many isomorphism classes of simple objects (= “primary CFT fields”).
I am also only going from my memory of the talk. The reason that rational TQFT’s couldn’t distinguish everything had something to do with roots of unity. (Specifically, with twisting kn times, where we were working with nth roots of unity.) That’s compatible with Urs’ statement above that rational TQFT’s should have finitely many isomorphism classes of simple object. It seems very restrictive though — surely topologists work with quantum groups at general values of q all the time, yes?
In general I wouldn’t know what you might want to mean by an “object of a TQFT” (I could make up a sensible definition, but maybe it would not coincide with what you have in mind here).
The way the finiteness assumption enters most directly into the Reshitikhin-Turaev construction is as follows: the RT 3-functor is defined not just on 3d cobordisms, but on “extended 3d-cobordisms” which are equipped with extra data: each 2-d surface may have “marked points” which are colored by a simple object of the modular tensor category. Then inside the 3-d cobordisms there are ribbons running which connect these marked points (the Wilson lines of CS theory!).
The way the Reshitikhin-Turaev 3d TFT functor is defined goes like this: to each surface with marked points it assigns the vector space
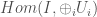of morphisms in the modular category from the tensor unit to the direct sum of the labelling simple objects.
Given a 3-d manifold, the functor is evaluated on it by first determining the surgery of the 3-sphere needed to obtain that manifold. Then there is a rule for how this surgery induces a certain knot to be drawn inside the 3-spere. That knot is included with the Wilson line ribbons we had previosuly. Then there is a formula which tells you how to label all these ribbons by morphisms in the modular tensor category, sum up the result, and finally obtain a linear map
from input to output given by postcomposition with that sum of morphisms in C.
It’s a rather unilluminating procedure, I must say. In any case, it involves summing over isomorphism classes of simple objects. If there are finitely many such, everything is well defined and one proves that the result really defines a cobordism rep. If not, nobody knows how to make sense of this prescription.
So that’s, as far as I understand, where semisimplicity enters the RT 3d TFT. I don’t know what it would mean to take an arbitrary TFT and ask if it is “rational” or “semisimple”. But that’s just me, probably somebody does have a sensible definition for that.
Sorry, I misspoke: Reshitikhin-Turaev don’t have a 3-functor, but a 1-functor on 3-d cobordisms, of course.
(But there should be a 3-functor refining it…)
Noah,
My source (Bakalov & Kirrilov) defines modular tensor categories as semisimple ribbon categories with finitely many simple objects satisfying blah blah. Perhaps this is abnormal. But I think the concepts here are clear enough; we seem to be confused only about terminology.
David,
This point has always confused me, but I think Schechtman and Varchenko showed that the braiding in quantum groups “comes from” the KZ equation, which lives on a configuration space of points (or boundary circles) on a curve. Dehn twists are loops in M_g, and the braiding doesn’t see that part of the fundamental group of the universal curve. You can get connections on the base by Beilinson-Bernstein descent, but I don’t know what relation that has to your choice of q.
It’s clear, but just for the record: it’s finitely many isomorphism classes of simple objects.
Urs,
Right. Thanks!
Scott, David, Joel,
Part of the confusion comes from the fact that topologist study both knots and three manifolds. These are intimately related, but are not exactly the same thing.
If you are interested in invariants of knots and links (let’s say framed links) then what you want is to look at ribbon categories. There is a general construction that lets you get link invariants out of such categories. Basically the usual “graphical calculus” will give you an invariant of a “colored” (framed) link via its projection to the plane. Here we color the link by the objects of our category. If our category had finitely many simple objects we could do some sort of summation over simples to get (framed) link invariants. For this quantum groups at general q work, and this is one way you get things like the Jone’s polynomial.
But now let’s suppose that you like 3-manifolds and not knots. What can you do? Well if you are given a framed link, you can view it in the 3-sphere and do surgery to get a 3-manifold. Maybe our invariant of a link is an invariant of the 3-manifold? The problem is that different links can give the same 3-manifold. You’ll need an invariant which is invariant under the Kirby calculus moves. So already you see that we need more then just a ribbon category. Let’s go for the gold and ask that our invariant is actually part of a TQFT, can we do this?
The answer is “yes” and “no”. If what you want is an honest invariant and an honest functor from the category of bordisms to vector spaces, then the answer is usually no. But if you allow for projective TQFTs (which I won’t explain yet), then there is a general machine. The input is a special kind of ribbon category called a modular tensor category and the construction of the TQFT is similar to the link invariant construction above. It also generalizes to more exotic situations where you have 3-manifolds with colored (framed=ribbon) links inside them. This is what Urs was alluding to in 12.
So now, how do we get such MT categories? We’ll as far as I understand it quantum groups at general q don’t work. However at a root of unity you can do something. At a root of unity, the representation category is bad, but it has a nice quotient. This quotient is a MT category and so feeds into the general machine to give a TQFT.
Urs, Noah, A. J.,
There is also a notion of modular tensor category where you don’t require things to be semi-simple. Is it possible to build TQFTs out of these? The answer is “kinda”.
The construction I’m thinking of is described in the book “Non-semisimple Topological Quantm Field Theories for 3-Manifolds with Corners” by Kerler and Lyubashenko.
Part of the problem is that this is all tied up “projective” TQFTs and what sort of “projective anomalies” you allow. As I understand it, in the non-semisimple case you need really bad ones which can make your TQFT take unexpected zero values. For example, one of these TQFTs gives zero for the value of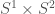
.
For those less savvy in 3D TQFTs the value of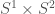
should be the trace of the identity map on the vector space for 
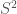. In their example it vanishes because of this weird “half-projective” anomaly.
There is more to say, maybe I should write a post on 3D TQFTs…
Thanks. I wasn’t aware of that.
Please do, I’d be intersted.
When thinking about 3d TQFT’s whose associated braided tensor categories are not semisimple, the best example is Rozansky-Witten theory, as y’all probably know. References are “Rozansky-Witten Theory” (arXiv:math/0112209) by Justin Roberts as well as “On the Rozansky-Witten weight systems” (arXiv:math/0602653) by said Mr Roberts and my good supervisor Simon Willerton.
In Rozansky-Witten theory, you fix a holomorphic symplectic manifold X, and the category associated to the circle is the graded derived category D(X). The theorem is that this can be given a ribbon structure… but its not semisimple. So its an example of a “non-semisimple” modular category… even though that doesn’t make sense according to the traditional definition, of course.
This stuff isn’t completely understood… at least I certainly don’t understand it! But it’s clear that Rozansky-Witten forms a great example of a “non-semisimple 3d TQFT” and we need to make sure that any new definitions we make will fit this example.
I don’t know much about the TQFT aspect, but nonsemisimple versions of modular tensor categories seem to arise from logarithmic conformal field theories. The term “logarithmic” here comes from the log q terms that may appear in the characters of nontrivial extensions of modules over, say, a vertex algebra describing the theory. Presumably, one could get such a vertex algebra from something like chiral differential operators on a holomorphic symplectic manifold X (see Bruce’s comment), but I’m very fuzzy on this.
Normally, the characters are found by a weighted trace of an operator L_0 (more precisely, it is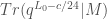
) coming from the conformal structure, but nontrivial extensions allow L_0 to act with nontrivial Jordan blocks, and this is accounted for using log terms. A more geometric interpretation is that characters of modules (conjecturally) span the space of q-expansions of genus one conformal blocks (possibly with an eta-function multiplier). The conformal blocks form a bundle with (projective) connection on the space of genus one curves, and as the curves degenerate to a nodal cubic, the flat sections can be written as formal solutions to some differential equations.
There is a hypothesis of factorization that identifies some of these solutions as characters of modules, by specifying an isomorphism between the genus one conformal blocks near the boundary of the moduli space and genus zero blocks with dual module insertions at the preimage of the node under the normalization map. Much of this has been proved in special cases, but the general picture is still sketchy. I suspect nonsemisimplicity is related to nonvanishing higher chiral homology on a genus zero curve, but there doesn’t seem to be any literature on that.
Bruce,
thanks a lot for the useful remark about Rozansky-Witten.
Concering that remark I made
at the end of 12 I should add that in saying so, I was thinking of the 1-functorial formulation where data is assigned only to top and top minus one dimension.
In our comment you essentially say that when we have actually an extended TQFT, which assigns data to manifolds of all dimensions, we can say it is semisiple if the categories it assigns to top minus two dimensional manifolds is.
Okay, good. In that case let’s go one step further:
we should admit then that if an abelian monoidal category is semisimple, it may be regarded as a 2-vector space of finite dimension. That’s of course a major emphasis of your (Bruce’s) work, I am just saying it for the record here.
So if we are talking about extended TQFT, we might actually want to say:
Definition An extded n-dimensional TQFT is finite dimensional if all the k-vector spaces assigned to (n-k)-dimensional manifolds are of finite dimension.
(i.e. the usual notion of finiteness in representation theory, keeping in mind that an extended TQFT is a representation of a cobordism n-category.)
And then we say: “suppose we have a finite dimensional TQFT” instead of: “suppose we have a semisimple TQFT”.
Dear moderators,
I just sent another message which apparently did not pass the spam filter’s scrutiny. I’d be grateful if you could resurrect it.
(I am wondering what about my commenting style it is that makes the robot suspect that all I really want is to sell [something I can’t name lest this message won’t go through either] to you all…)
I think the issue of semisimplicity is a reflection of trying
to make TFTs in an abelian setting, rather than following
the physicists lead and making them in a derived setting.
(as far as I know Chern-Simons is about the only example
in physics of a TFT which is not formulated in a differential
graded fashion). More precisely TFTs (such as Rozansky-Witten,
Seiberg-Witten, “geometric Langlands”, etc) arise
typically from twisting supersymmetric quantum field theories,
meaning we have an underlying graded (or at
least Z/2 graded) vector space with a differential Q,
which is part of our SUSY algebra that’s survived the twisting.
This means that in codim one you really have a dg vector
space, in codim two a dg category, etc.
In an abelian setting you can find that the
modules associated to codim one manifolds are forced to be
surjective, and some kind of semisimplicity is forced
in codimension two.
But if you look at TFTs in a dg or other suitably homotopical
setting there are no such restrictions. Fully extended TFTs
always satisfy some strong “finite dimensionality” (or more
precisely, dualizability) hypotheses, but for example
the derived category of coherent sheaves
on any smooth projective variety satisfies a strong
form of these and is far from semisimple.
On the other hand, it is also not quite natural to restrict attention to TQFTs and to QFTs of low dimension, only because these are the more accessible examples.. Every QFT should come from a rep of cobordisms with suitable extra structure.
So in particular the 2d SCFTs which give rise, via twists, to 2d TFTs are themselves cobordisms reps (namely of 2-cobordisms with conformal structure — for the bosonic rational case this has been made fully precise, the susy and non-rational cases are bound to work in a similar fashion).
This gives another large class of examples of cobordism reps which take values in things that are not dg-enriched.
And in principle, even though nothing much seems to be known about it, one has Chern-Simons theories in higher dimensions, each of them coming from a transgressive cohomology class on the group in question. And each of these (as also suggested by physics, for that matter) should have a “holographically” related higher dimensional CFT “on its boundary”. And, while precise details are essentially unknown, there does not seem to be a reason to expect that any of these higher CS/CFT pairs live in the dg-world a priori.
What I am lacking is a good general intuition for what the twisting of susy CFTs to topological theories means on general abstract grounds. It’s usually introduced as a trick: “look, we can do the following and the result is interesting” without much or any motivation for what it means to “do the twist”.
Well, you possibly have more insight here than I do. But I am just thinking that understanding what twisting really means might go a long way towards explaining how dg-enrichment fits into the grand picture. After all, dg-enrichment can be regarded as enrichment over infinity-vector spaces, so if we have a sequence
dg-category , dg-2-category, etc.
we really seem to be looking at a categorificatoin in two different directions, as with bisimplicial sets.
That must mean something more profoundly than seems to be apparent. I don’t know what. Maybe you do.
I don’t think there’s anything mysterious about twisting —
it’s basically a physicist’s way of saying that we start with
a naive theory (one “in coordinates”), and then we realize
we can make the fields live in various natural bundles
(ie ones associated to the symmetry group of the theory,
typically some superPoincare or superconformal group)
rather than being plain scalars or spinors etc.
A mathematician might skip the 0-th step and just say
consider a theory with the following fields living in
various bundles.
Given such a (“twisted”) supersymmetric theory,
we can then study what are the conserved supercharges Q.
The space of these Q’s tells us all the ways in particular
to make a topological field theory from our SUSY QFT,
and the result comes in a dg flavor by construction.
I have learned only very recently (embarrassing!) to appreciate
the incredible depth and importance of the
study of the possible supersymmetric field theories,
which the physicists have done so well. It really seems
to cover so much of the math we’re interested in, eg
the study of SUSY gauge theories really seems to know
ALL the structures we care about in representation theory
in characteristic zero. So I personally don’t see much motivation
to work in greater generality than what the physics already gives
us, rather than to try to understand the structures we’re given.
Witten has explained for example
how all the subtlest aspects of geometric Langlands
come from classifying supersymmetries and twistings
in N=4 d=4 super-Yang-Mills, but that this is only
a pale reflection of a superconformal 6d CFT,
which itself is but a pale reflection of 10d strings
or 11d M-theory. I think just understanding
the implications of this for representation theory
will take longer than I can dream.
Regarding dg structure: I don’t know anything about
nontopological QFT, but the point is that
cobordism categories are topological, and differential
graded structure is the simplest way we know
to algebraize topological spaces (in characteristic zero).
From this POV dg stuff is completely interchangeable
with any other context that’s rich enough to sense
topology. To understand nontopological
field theory one would have to have a good idea
of how to measure spaces of cobordisms with
complex structures or metrics or so on the way
we know how to measure topology, which
is certainly beyond what I can understand.
Urs, I agree with you about finite-dimensional abelian categories, etc., but we should also remember that in these 3d TQFTs like Rozansky-Witten theory, the category we want to associate to the circle is not an abelian category, its the derived category. I don’t really know what that really means, but it indicates we will have to rethink a bit the Baez-Dolan `Extended TQFT Hypothesis part II’ which says that extended TQFT’s are n-functors from nCob into nHilb. In the most naive reading of that hypothesis, it would mean that the category associated to the circle should be some kind of abelian category, which is not the case. Something somewhere needs to be jigged a bit.
Bruce – an appropriately homotopically “jigged version” of the extended TQFT hypothesis was presented by Jacob Lurie in the Morse lectures at the IAS (notes at http://www.math.utexas.edu/users/benzvi/GRASP/lectures/IASterm.html)
— Hopkins and Lurie have proved this version in dimensions 1 and
2 (where it generalizes a theorem of Costello by replacing
the target of the functor 2Cob–> dg-categories by
an arbitrary 2-category), and have tentatively
announced (in the last lecture) they expect a proof in arbitrary dimension… exciting times!
Just to prevent miscommunication, I think you mean (oo,2) category, right? Though I assume everyone will be dropping the infinity-commas in the nearish future :).
David,
Thanks for putting up the notes. They are very helpful. Unfortunately, when I read them on my mac, the images are confined to the bottom left quarter of each page, so I have to squint or zoom in. Is this a known problem?
Jacob’s rephrasing of the Baez-Dolan hypothesis is pretty neat, since the target is made essentially irrelevant. If framed nCob is freely generated by one object, the endomorphisms of that object should form an interesting n-category with respect to universal properties, since it acts on all TQFTs.
Aaron – yes, I mean (oo,2)-category (yes I agree
before we know it we will be meaning (oo,-) in front of everything,
and dropping it!)
Scott – I think it should work better with Firefox maybe?
I use firefox on the PC and there’s no such issue but other
browsers do funny things. The problem is I do something
incredibly stupid with the notes — I write them on the tablet
in Windows Journal format (jnt), save it as tiff, and
then convert it to pdf brutally, resulting in huge files..
suggestions welcome!
Thanks for pointing me to these notes David, they are a treasure trove! There are a few points my philosophy differs slightly though. It seems to me that Jacob Lurie’s programme is very much a generators/relations programme. In the first lecture, he paraphrases the Baez-Dolan cobordism hypothesis to say that
Cobordism hypothesis (paraphrased): Extended TQFTs are “easy to describe and build”.
By the way, as far as I know Baez and Dolan didn’t explicitly write down a “Cobordism hypothesis”, although perhaps they should have. Instead they wrote down the “Extended TQFT hypothesis I” which is a bit confusing. If we rename that to the “Cobordism hypothesis”, then it basicaly says:
Cobordism hypothesis (original, basically): The n-category nCob is the free stable weak n-category with duals on one object.
Personally, I would disagree a bit with Jacob Lurie’s paraphrasing of it… I view the Cobordism hypothesis as a statement of the equivalence of topological concepts (manifolds, cobordisms, etc.) with algebraic ones (higher categories with duals). Each side can inform the other, but I don’t think the Cobordism hypothesis makes it appreciably easier to explicitly understand nCob. In particular I don’t think it makes it any easier to write down a TQFT… in dimension greater than 3 at least, because that’s where the generators/relations game becomes too difficult.
Instead, I go along with the viewpoint which Dan Freed also stresses in the MSRI talk available on his webpage. Namely, that in the realm of TQFTs it is better to write down what he calls “a priori” TQFTs, instead of using a generators/relations argument. In other words, one should write down a geometric construction which a priori captures the gluing laws of the path integral for any manifold (and some other laws perhaps yet to be elucidated)… and then you will have an extended TQFT. At THAT point you check what it assigns to the circle (not the other way round).
Let me summarize my point. It is often said, for instance, that “2d TQFTs come from Frobenius algebras”. Instead I think it is better to say “2d TQFTs give rise to Frobenius algebras”.
Above, I meant “dimension greater than or equal to 3”, sorry about that.
Here is a question I have arising from Jacob Lurie’s notes, perhaps someone here can help me out. In the last lecture, near the end, he points out, roughly, that the target 2-category of a TQFT should have duals for objects, morphisms and 2-morphisms.
Now, he says that dgCat_k has duals for morphisms provided we restrict our dg-categories to those of the form QCoh(X) where X is smooth and proper. Now this is something I’d love to get to the bottom of, since I have come across it a lot. My understanding is that by “dual for morphism in a 2-category” in this TQFT setting, we mean a morphism which has a simultaneous left and right adjoint… because that is the case in 2Bord.
But that doesn’t hold for these morphisms between dg-categories of the form QCoh(X), right?
My bible on this is the paper by Willerton and Calderaru on the Mukai pairing. There they employ the 2-category Var (which it seems to me Jacob Lurie is essentially restricting to), and show that the Serre kernel allows us to equip every morphism with a left and right adjoint (but these aren’t the same). So Var is not a 2-category with duals… in the strong sense we apparantly need.
Bruce,
I think Jacob is claiming this makes TFTs much easier to write down –
if you are given an (infty,n) category with duals in an appropriately strong sense, then to give a TFT valued in it in any dimension
is equivalent to just giving a single object, no other relations.
But maybe I misunderstood your objection – it is indeed
hard to find categories with all these duals..
I also am not sure what you meant about Jacob restricting to the
2-category Var – by a theorem of Toen functors between QC(X)
and QC(Y) are given by QC(X x Y) for X,Y arbitrary varieties, so there is no restriction.. for smooth projective varieties the same is true
for coherent sheaves.
You raise a very interesting/troubling point about the fact that adjoints of functors between QC(X) and QC(Y) – the left and right don’t agree, but they differ by an orientation (Serre duality). The last couple of pages in the notes was things he was saying informally at
the blackboard after the talk and I probably misunderstood..
in the 2d field theory case then we want a Calabi-Yau variety,
which guarantees left and right adjoints agree up to a shift
(which you can incorporate into your structure using a 2-gerbe
as he says, or as Costello says in a slightly different way).
Of course we don’t actually need CY varieties, the 2-category of CY categories (ones that look like sheaves on CYs) will be an example
of a 2-category with strong duals in the sense we need (up to twisting by this 2-gerbe). In general the left and right adjoints will differ by an orientation (Serre functor) for smooth proper varieties, and you’d have to twist this away in some way to get a TFT..
Ok, thanks David I see your point now. I indeed had some misconceptions… Lurie’s philosophy is indeed not about generators and relations, as I was suggesting. I have learnt something here.
But I think there is a nugget of truth to what I was saying. It seems to me that the cobordism hypothesis only makes extended TQFTs easier to write down when the dimension is low enough (less than or equal to 2) so that we can explicitly understand the n-category in which the single object is living. However, for 3d TQFTs this means our object (the object assigned to a point) will be living in a 3-category. For example, in Rozansky-Witten theory, the gismo assigned to a point is something like “the 2-category of coherent stacks on X” (whatever that means!); this 2-category is itself an object in some “3-category of gismos”…. this is the 3-category with duals that we are talking about. My point is that its pretty darn tough to understand these things precisely… what on earth is a 3-category with duals, for instance? Remember, we need the fully weak versions of these things, because that’s what arises in geometrical situations. Luckily that’s where the $(\infty, n)$ homotopy methods can probably help out.
The reason all these complications about 3-categories and so on don’t show up in Lurie’s talk, is that he takes 3d TQFTs and “dimensionally reduces” them to 2d TQFTs by setting $Z’ (M) = Z(M \times S^1)$. For instance, he simplifies Chern-Simons theory into a 2d TQFT which assigns to the circle the twisted equivariant K-theory of G (in the full 3d Chern-Simons theory this is what is assigned to the torus). That’s fine, and its an important simplification, but if we are to generate any new quantum invariants of 3-dimensional manifolds, we really want 3d TQFTs, and then we have to deal with 3-categories and so on.
In other words, the Cobordism hypothesis only helps us to write down TQFTs if we truly have a good grip on the theory of higher categories with duals (here “higher” means $n \geq 3$). My understanding though is that we are far from that point; I had the impression that even Lurie’s methods have yet to really “tame” these guys. Maybe I am a few years behind the times.
By the way, thanks for your comments on duals:
“the 2-category of CY categories (ones that look like sheaves on CYs) will be an example of a 2-category with strong duals in the sense we need (up to twisting by this 2-gerbe).”
That’s great, that’s what I was hoping, that there was some way to get this to work. Now I need to understand some deeper abstract formulation of this “twisting by the 2-gerbe” mechanism…
Was offline for a while, so much has happened here.
Bruce wrote:
Is this just taken from David’s comment or is there a document describing what exactly this is about?
It should be the return to Freed’s “a priori TQFT” picture: Chern-Simons theory (if that’ still what we are talking about) is given by a Chern-Simons 2-gerbe with connection on BG and the Chern-Simons TQFT is obtained by “quantizing” that.
If one first discusses this for a CS 2-gerbe of trivial class then passing to nontrivial classes afterwards looks like one is “twisting” the trivial case. (By the way, I’d second Jim Stasheff here: if we can, we should not say “twist”. There are billions of things that deserve to be called twists. So none does. It is just not descriptive enough. In my himbe experience, when we have a structure and find that we need to “twist” it, it is an indication that we are still missing a bigger picture. )
I think that the general picture of Freed’s “a priori QFTs” (which we could just call “Sigma-models”!) involves starting with a differential cocycle on some target space and turning that into a differential cocycle on some abstract cobordism. The assignments to circles, tori, etc, are then obtained from taking the corresponding holonomies of that latter differential cocycle.