A few weeks ago, I e-mailed Will Sawin excitedly to tell him that I could extend the new bounds on three-term arithmetic progression free subsets of 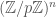 to
to  . Will politely told me that I was the third team to get there — he and Eric Naslund already had the result, as did Fedor Petrov. But I think there might be some expository benefit in writing up the three arguments, to see how they are all really the same trick underneath.
. Will politely told me that I was the third team to get there — he and Eric Naslund already had the result, as did Fedor Petrov. But I think there might be some expository benefit in writing up the three arguments, to see how they are all really the same trick underneath.
Here is the result we are proving: Let 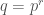 be a prime power and let
be a prime power and let 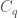 be the cyclic group of order
be the cyclic group of order  . Let
. Let 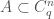 be a set which does not contain any three term arithmetic progression, except for the trivial progressions
be a set which does not contain any three term arithmetic progression, except for the trivial progressions 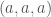 . Then
. Then
![\displaystyle{|A| \leq 3 | \{(m^1, m^2, \ldots, m^n) \in [0,q-1]^n : \sum m^i \leq n(q-1)/3 \}|.}](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle%7B%7CA%7C+%5Cleq+3+%7C+%5C%7B%28m%5E1%2C+m%5E2%2C+%5Cldots%2C+m%5En%29+%5Cin+%5B0%2Cq-1%5D%5En+%3A+%5Csum+m%5Ei+%5Cleq+n%28q-1%29%2F3+%5C%7D%7C.%7D&bg=ffffff&fg=444444&s=0&c=20201002)
The exciting thing about this bound is that it is exponentially better than the obvious bound of  . Until recently, all people could prove was bounds like
. Until recently, all people could prove was bounds like  , and this is still the case if
, and this is still the case if  is not a prime power.
is not a prime power.
All of our bounds extend to the colored version: Let 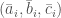 be a list of
be a list of  triples in
triples in 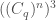 such that
such that  , but
, but 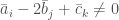 if
if 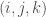 are not all equal. Then the same bound applies to
are not all equal. Then the same bound applies to  . To see that this is a special case of the previous problem, take
. To see that this is a special case of the previous problem, take 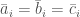 . Once the problem is cast this way, if
. Once the problem is cast this way, if  is odd, one might as well define
is odd, one might as well define 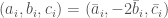 , so our hypotheses are that
, so our hypotheses are that 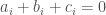 but
but 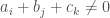 if
if 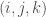 are not all equal. We will prove our bounds in this setting.
are not all equal. We will prove our bounds in this setting.
My argument — Witt vectors
I must admit, this is the least slick of the three arguments. The reader who wants to cut to the slick versions may want to scroll down to the other sections.
We will put an abelian group structure  on the set
on the set  which is isomorphic to
which is isomorphic to 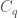 , using formulas found by Witt. I give an example first: Define an addition on
, using formulas found by Witt. I give an example first: Define an addition on 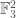 by
by
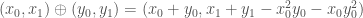
The reader may enjoy verifying that this is an associative addition, and makes 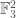 into a group isomorphic to
into a group isomorphic to  . For example,
. For example, 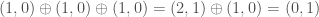 and
and 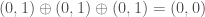 .
.
In general, Witt found formulas
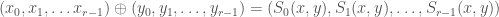
such that  becomes an abelian group isomorphic to
becomes an abelian group isomorphic to 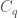 . If we define
. If we define 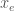 and
and  to have degree
to have degree 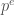 , then
, then  is homogenous of degree
is homogenous of degree 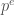 . (Of course, Witt did much more: See Wikipedia or Rabinoff.)
. (Of course, Witt did much more: See Wikipedia or Rabinoff.)
Write
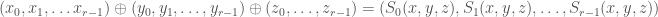 .
.
and set
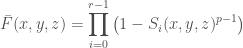 .
.
For example, when 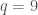 , we have
, we have
 .
.
So 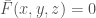 if and only if
if and only if 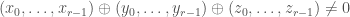 in
in 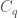 .
.
We now work with 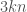 variables,
variables,  ,
, 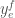 and
and 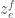 , where
, where  and
and  . Consider the polynomial
. Consider the polynomial
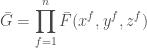 .
.
Here each 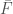 is a polynomial in
is a polynomial in  variables.
variables.
So 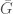 is a polynomial on
is a polynomial on 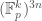 . We identify this domain with
. We identify this domain with 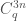 . Then
. Then 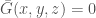 if and only if
if and only if 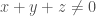 in the group
in the group 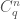 .
.
We define the degree of a monomial in the  ,
, 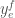 and
and 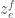 by setting
by setting 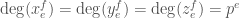 . In this section, “degree” always has this meaning, not the standard one. The degree of
. In this section, “degree” always has this meaning, not the standard one. The degree of  is
is 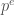 ; the degree of
; the degree of 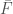 is
is 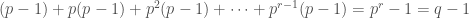 and the degree of
and the degree of 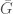 is
is 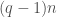 .
.
From each monomial in 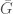 , extract whichever of
, extract whichever of 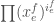 ,
, 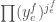 or
or 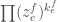 has lowest degree. We see that we can write
has lowest degree. We see that we can write
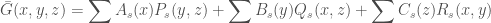
where 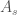 ,
, 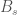 and
and  are monomials of degree
are monomials of degree 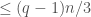 .
.
The now-standard argument (I like Terry Tao’s exposition) shows that  is bounded by three times the number of monomials
is bounded by three times the number of monomials 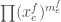 of degree
of degree 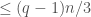 . One needs to check that the argument works when the “degree” of a variable need not be
. One needs to check that the argument works when the “degree” of a variable need not be 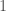 , but this is straightforward.
, but this is straightforward.
Except we have a problem! There are too many monomials. To solve this issue, let 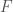 be the polynomial obtained from
be the polynomial obtained from 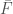 by replacing every monomial
by replacing every monomial 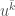 by
by 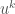 where
where 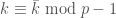 with
with 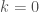 if
if  and
and 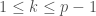 if
if  . So
. So 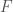 coincides with
coincides with 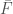 as a function on
as a function on  , but
, but 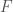 uses smaller monomials. For example, the reader who multiplies out the expression for
uses smaller monomials. For example, the reader who multiplies out the expression for 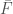 when
when 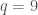 will find a term
will find a term 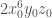 . In
. In 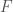 , this is replaced by
, this is replaced by 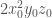 . The polynomial
. The polynomial 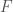 does not have the nice factorization of
does not have the nice factorization of 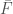 , but it is much smaller. For example, when
, but it is much smaller. For example, when 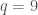 ,
, 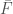 has
has 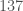 nonzero monomials and
nonzero monomials and 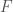 has
has 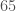 . Replacing
. Replacing 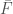 by
by 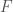 can only lower degree, so
can only lower degree, so 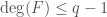 . Now rerun the argument with
. Now rerun the argument with 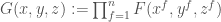 . Our new bound is three times the number of monomials
. Our new bound is three times the number of monomials 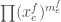 of degree
of degree 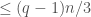 , with the additional condition that all exponents
, with the additional condition that all exponents 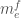 are
are  .
.
Now, the monomial  has degree
has degree 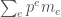 . Identify
. Identify ![[0,p-1]^r](https://s0.wp.com/latex.php?latex=%5B0%2Cp-1%5D%5Er&bg=ffffff&fg=444444&s=0&c=20201002) with
with ![[0,q-1]](https://s0.wp.com/latex.php?latex=%5B0%2Cq-1%5D&bg=ffffff&fg=444444&s=0&c=20201002) by sending
by sending 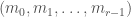 to
to 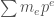 . We can thus think of
. We can thus think of ![[0,p-1]^{rn}](https://s0.wp.com/latex.php?latex=%5B0%2Cp-1%5D%5E%7Brn%7D&bg=ffffff&fg=444444&s=0&c=20201002) as
as ![[0,q-1]^n](https://s0.wp.com/latex.php?latex=%5B0%2Cq-1%5D%5En&bg=ffffff&fg=444444&s=0&c=20201002) . We get the bound
. We get the bound ![N \leq 3 | \{(m^1, m^2, \ldots, m^n) \in [0,q-1]^n : \sum m^i \leq n(q-1)/3 \}|](https://s0.wp.com/latex.php?latex=N+%5Cleq+3+%7C+%5C%7B%28m%5E1%2C+m%5E2%2C+%5Cldots%2C+m%5En%29+%5Cin+%5B0%2Cq-1%5D%5En+%3A+%5Csum+m%5Ei+%5Cleq+n%28q-1%29%2F3+%5C%7D%7C&bg=ffffff&fg=444444&s=0&c=20201002) , just as in the prime case.
, just as in the prime case.
Naslund-Sawin — binomial coefficients
Let’s be much slicker. Here is how Naslund and Sawin do it (original here).
Notice that, by Lucas’s theorem, the function 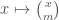 is a well defined function
is a well defined function 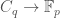 when
when  . Moreover, using Lucas again,
. Moreover, using Lucas again,
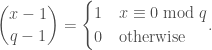
Define a function  by
by
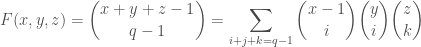
 .
.
Here we have expanded by Vandermonde’s identity and used 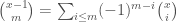 .
.
Define a function  by
by 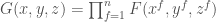 just as before. So
just as before. So 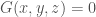 if and only if
if and only if 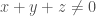 in the abelian group
in the abelian group 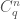 . Expanding
. Expanding 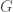 gives a sum of terms of the form
gives a sum of terms of the form 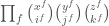 . Considering such a term to have “degree”
. Considering such a term to have “degree” 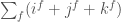 , we see that
, we see that 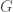 has degree
has degree  .
.
As in the standard proof, factor out whichever of 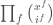 ,
,  or
or 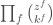 , has least degree. We obtain
, has least degree. We obtain
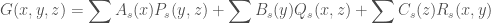
where 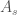 ,
, 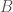 and
and 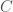 are products of binomial coefficients and, taking
are products of binomial coefficients and, taking 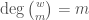 , we have
, we have 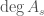 ,
, 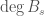 and
and 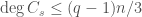 .
.
We derive the bound ![N \leq 3 | \{(m^1, m^2, \ldots, m^n) \in [0,q-1]^n : \sum m^f \leq n(q-1)/3 \}|](https://s0.wp.com/latex.php?latex=N+%5Cleq+3+%7C+%5C%7B%28m%5E1%2C+m%5E2%2C+%5Cldots%2C+m%5En%29+%5Cin+%5B0%2Cq-1%5D%5En+%3A+%5Csum+m%5Ef+%5Cleq+n%28q-1%29%2F3+%5C%7D%7C&bg=ffffff&fg=444444&s=0&c=20201002) , exactly as before.
, exactly as before.
Group rings — Petrov’s argument
I have taken the most liberties in rewriting this argument, to emphasize the similarity with the other arguments. The reader can see the original here.
Let 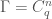 . Let
. Let 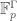 be the ring of functions
be the ring of functions 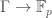 with pointwise operations, and let
with pointwise operations, and let ![\mathbb{F}_p[\Gamma]](https://s0.wp.com/latex.php?latex=%5Cmathbb%7BF%7D_p%5B%5CGamma%5D&bg=ffffff&fg=444444&s=0&c=20201002) be the group ring of
be the group ring of 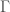 . We think of
. We think of ![\mathbb{F}_p[\Gamma]](https://s0.wp.com/latex.php?latex=%5Cmathbb%7BF%7D_p%5B%5CGamma%5D&bg=ffffff&fg=444444&s=0&c=20201002) acting on
acting on 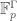 by
by 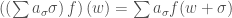 .
.
Let  ,
, 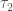 , …,
, …, 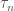 be generators for
be generators for 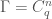 . Let
. Let  the functions annihilated by the operators
the functions annihilated by the operators 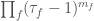 where
where 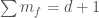 . For example,
. For example, 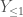 is the functions
is the functions 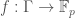 which obey
which obey 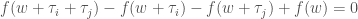 for any
for any 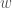 ,
,  and
and 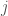 . We think of
. We think of 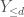 as polynomials of degree
as polynomials of degree 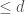 , and the dimension of
, and the dimension of 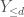 is the number of monomials in
is the number of monomials in 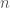 variables of total degree
variables of total degree 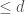 where each variable has degree
where each variable has degree 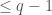 .
.
Define 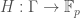 by
by 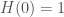 and
and  otherwise. Define
otherwise. Define 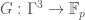 by
by  .
.
We write 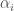 ,
,  and
and  for the generators of the three factors in
for the generators of the three factors in 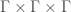 .
.
Then we have
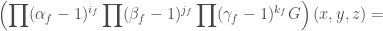
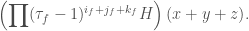
So, if 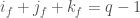 , then
, then 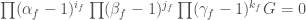 as a function on
as a function on  .
.
On the other hand, we can expand 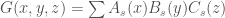 for
for 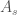 ,
, 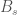 and
and  in
in 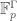 . We see that, if
. We see that, if 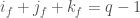 , then
, then
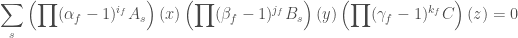 .
.
We make the familiar deduction: We can write 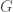 in the form
in the form
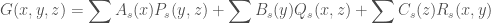
where 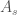 ,
, 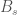 and
and  run over a basis for
run over a basis for  .
.
Once more, we obtain the bound  .
.
Petrov’s method has an advantage not seen in the other proofs: It generalizes well to the case that 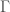 is non-abelian. For any finite group
is non-abelian. For any finite group 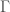 , let
, let 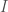 be a one-sided ideal in
be a one-sided ideal in ![\mathbb{F}_p[\Gamma]](https://s0.wp.com/latex.php?latex=%5Cmathbb%7BF%7D_p%5B%5CGamma%5D&bg=ffffff&fg=444444&s=0&c=20201002) obeying
obeying 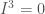 . In our case, this is the ideal generated by
. In our case, this is the ideal generated by 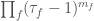 with
with 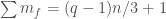 . Then we obtain a bound
. Then we obtain a bound ![N \leq 3 \dim \mathbb{F}_p[\Gamma]/I](https://s0.wp.com/latex.php?latex=N+%5Cleq+3+%5Cdim+%5Cmathbb%7BF%7D_p%5B%5CGamma%5D%2FI&bg=ffffff&fg=444444&s=0&c=20201002) for sum free sets in
for sum free sets in 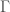 .
.
What’s going on?
I find Petrov’s proof immensely clarifying, because it explains why the arguments all give the same bound. We are all working with functions 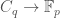 . I write them as polynomials in
. I write them as polynomials in  variables
variables 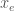 , Naslund and Sawin use binomial coefficients
, Naslund and Sawin use binomial coefficients 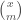 . The formulas to translate between our variables are a mess: For example, my
. The formulas to translate between our variables are a mess: For example, my 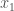 is their
is their 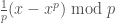 . However, we both agree on what it means to be a polynomial of degree
. However, we both agree on what it means to be a polynomial of degree 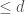 : It means to be annihilated by
: It means to be annihilated by  .
.
In both cases, we take the indicator function of the identity and pull it back to  along the addition map. The first two proofs use explicit identities to see that the result has degree
along the addition map. The first two proofs use explicit identities to see that the result has degree  . The third proof points out this is an abstract property of functions pulled back along addition of groups, and has nothing to do with how we write the functions as explicit formulas.
. The third proof points out this is an abstract property of functions pulled back along addition of groups, and has nothing to do with how we write the functions as explicit formulas.
I sometimes think that mathematical progress consists of first finding a dozen proofs of a result, then realizing there is only one proof. My mental image is settling a wilderness — first there are many trails through the dark woods, but later there is an open field where we can run wherever we like. But can we get anywhere beyond the current bounds with this understanding? All I can say is not yet…