Local systems: the path groupoid approach

This is the first of the series of posts I promised, on different ways of getting local systems.

In this section, we’ll explain the approach which leads to étale sheaves. I’ll start out by describing the analogous ideas in the topological setting; and then sketch how to make them fully algebraic.

I’ve realized that I need a word for the data which I use to obtain a local system. Because I’m feeling uncreative, I’ll call it the input. Again, X is a space of some sort on which we want to build a local system.

For any two points x and y in X, let [x,y] denote the set of paths from x to y, modulo homotopy. By concatenating paths, we get a multiplication *: [x,y] \times [y.z] \to [x,z]. In particular, [x,x] is the fundamental group \pi_1(X, x).

Definition A.1: An A.1 input consists of a vector bundle V on X and, for every x and y in X and every path \gamma from x to y, an isomorphism \phi_{\gamma} : V_x \to V_y, such that \phi_{\gamma} \circ \phi_{\gamma'} = \phi_{\gamma * \gamma'}.

Let \mathcal{V} be an A.1 local system and let U be an open subset of X. Define \Gamma(U,\mathcal{V}) to be the vector space of sections \sigma : U \to \mathcal{V}|_U such that \phi_{\gamma}(\sigma(u)) = \sigma(v), for u and v are any two points of U and \gamma is any path from u to v that stays within U. Notice that, if U is a ball, then the dimenion of \Gamma(U,\mathcal{V}) is the rank of \mathcal{V}. Also, V \supset U is a containment of two balls, then the restriction map \Gamma(U, \mathcal{V}) \to \Gamma(V, \mathcal{V}) is an isomorphism.

There is a general philosophy in mathematics that a bundle can be recovered from knowing its sections over open sets. The key technical definition here is that of a sheaf.
So here is a definition which uses the \Gamma‘s.

Definition A.2 An A.2 input of rank n is the data of (1) for U any open subset of X, a vector space \Gamma(U) and (2) for any inclusion U \supset V of open sets, a map \rho_{UV}: \Gamma(U) \to \Gamma(V). It is required that (1) (\Gamma, \rho) satisfy the axioms of a sheaf (2) whenever U is a ball, \Gamma(U) is an n-dimensional vector space and (3) whenever U \supset V is a containment of balls, \rho_{UV} is an isomorphism.

This is the definition wikipedia gives for a local system.

Making this definition algebraic: To make this definition algebraic, one modifies definition A.2. Open sets are replaced by étale maps.

When working over \mathbb{C}, we can describe an étale map as an algebraic map i: U \to X such that, for any u \in U, we have some open neighborhood V of u such that i: V \to i(V) is a homeomorphism. (Notice that this definition is local on the source; if we made the definition local on the target, we’d be defining a covering space.)

The reason to introduce étale maps is that there aren’t enough Zariski open sets to “see” the topology of X but there are enough étale maps. For example, let X be \mathbb{C}^* and let’s try to see the nontrivial cycle. We cannot find Zariski open sets U_1, U_2 and U_3 with nonempty pairwise intersections, but triplewise empty intersection. However, we can find the N-fold cover of \mathbb{C}^* by itself. This latter étale map let’s us see that X has a cycle.

One has to rework the definition of a sheaf to work with maps rather than open sets. This is abstract but not difficult; the precise definition you need is that of a sheaf on a Grothendieck topology.

You’ll notice that there was no reason to work with real vector spaces here; vector spaces over a finite field would have done just as well in the topological discussion, and turn out to do much better once we shift to the fully algebraic setting. It is common to take X to be an algebraic variety over a field of characteristic p and V to be a bundle of vector spaces over a field of a different characteristic \ell. When you hear people talking about \ell-adic methods, that’s what they are talking about.

Finally, I’ll remark that there is a definition of the étale fundmental groupoid, and one could use this to mimic definition A.1. If you unfold what that definition means, however, you’ll see that you are really just working with definition A.2.

8 thoughts on “Local systems: the path groupoid approach”

  1. I have put a similar comment to the following on the ncatlab.

    Local systems for singular cohomology can also be seen as a special case of cohomology with coefficients in a crossed complex, and so related to homotopy classes of maps of spaces. Section 7. of the second paper below

    61. (with P.J. HIGGINS), “Crossed complexes and chain complexes
    with operators”, {\em Math. Proc. Camb. Phil. Soc.} 107 (1990)
    33-57.

    71. (with P.J.HIGGINS), “The classifying space of a crossed
    complex”, {\em Math. Proc. Camb. Phil. Soc.} 110 (1991) 95-120.

    is on local systems. The first paper relates crossed complexes and chain complexes with a groupoid of operators. The second paper proves a homotopy classification theorem, and in fact gives information on function spaces. Crossed complexes can be seen as giving the first step towards nonabelian cohomology.

    A module M over a groupoid G gives rise to a crossed complex K(M,n;G,1) which has M in dimension n and G in dimension 1, and trivial boundaries. But the category of crossed complexes has many conveniences, for example it is monoidal closed, and so has convenient notions of homotopy and higher homotopies.

    The above are downloadable from
    http://www.bangor.ac.uk/r.brown/publicfull.htm

  2. Pingback: Three ways of looking at a local system: Introduction and connection to cohomology theories « Secret Blogging Seminar ~

  3. When you redo everything for etale maps, what is the notion of ball? Affine schemes seems the most natural, but then there are pesky non-free projectives with flat connection, whose sections might not be of full dimension. Is it better to work with local schemes, or complete local schemes (the latter because of how nicely they play with the etale topology)?

  4. Greg,

    I think the correct analogue of balls is the formal neighborhoods of individual points. Of course, arguments of the form “I do everything on balls and then glue” have to be done a bit more carefully in this context, using infinitesimal information as well, so you end up having to think about flat connections on jet schemes and Harish-Chandra torsors. There’s a long discussion of this in the paper of Bezrukavnikov and Kaledin on algebraic Fedosov quantization.

  5. I’d like to elaborate just a bit. The notion of path translates well to the spectrum of a Henselian local ring, and one of the many equivalent formulations of the condition for a map to be formally étale (namely that deformations lift uniquely) is analogous to the uniqueness of path lifts for covering spaces. Actually, since the deformations in question don’t have to be from maps of points, it’s more like a general homotopy lifting property. Your typical affine scheme is too big to be contractible like a path [Edit: or a ball]. For example, if you puncture the affine line a couple times, it admits a lot of nontrivial local systems.

  6. Pingback: A semana nos arXivs… « Ars Physica ~

  7. @ David,

    Just a couple of typos:

    • In “Definition A.2” there is a $n$ when you probably meant to have a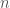 n; &

    • Two paragraphs below that, there’s a $u$ that should read u.

    Otherwise, excellent series!

    Cheers.

  8. Pingback: Three ways of looking at a local system: the infinitesimal perspective « Secret Blogging Seminar ~

Comments are closed.