Farey fractions, Ford circles, and SL_2.

The topic of this post came up during a conversation with some physicists about the fractional quantum Hall effect (which is quite fascinating, but I don’t feel particularly qualified to discuss).  I have decided to set it down here in the hope that, as long as I have an internet-capable device with me, I won’t have to rederive it in front of people again.  Some of this material appears in Apostol’s Modular functions and Dirichlet series in number theory and Conway’s The sensual form. I’d be happy to hear about other good treatments.

 

For each positive integer n, the Farey sequence F_n is the increasing sequence of rationals in [0,1] with denominator at most n. For example:

  1. F_1 = (0,1).
  2. F_2 = (0, \frac12 , 1)
  3. F_3 = (0, \frac13, \frac12, \frac23, 1)
  4. F_4 = (0, \frac14, \frac13, \frac12, \frac23, \frac34, 1)
  5. F_5 = (0, \frac15, \frac14, \frac13, \frac25, \frac12, \frac35, \frac23, \frac34, \frac45, 1)

It is a standard exercise in basic problem-solving classes to prove that they have the following two remarkable properties:

  1. Two rationals a/c > b/d in the unit interval are neighbors in some Farey sequence if and only if they satisfy ad-bc=1.
  2. If a/c and b/d are neighbors in the Farey sequence F_{\max(c,d)}, then they will remain neighbors in successive Farey sequences until they are separated by the fraction \frac{a+b}{c+d} in the sequence F_{c+d}.

These properties are typically proved using direct algebraic methods, but I’d like to describe a way to look at them geometrically. The geometric context is provided by Ford circles. Given a pair of coprime integers a,c, the Ford circle C(a,c) is the circle of radius \frac{1}{2c^2} centered at \frac{a}{c} + \frac{i}{2c^2} in the complex plane (except when c=0, where I will decree that it is the line \mathbb{R}+i together with an additional point called \infty). There is a minor ambiguity in identifying circles, since C(a,c) and C(-a,-c) are the same Ford circle. If we ignore the infinite case, the circle C(a,c) is tangent to the real line at the rational point a/c, and each rational number is contained in a unique circle.

There is an immediate connection between Ford circles and Farey fractions: the Farey sequence F_n is in bijection with the set of Ford circles that are tangent to the real line on the interval [0,1] and have radius at least \frac{1}{2n^2}. A less immediate connection is that Ford circles only intersect at tangent points (whose locations can be explicitly computed). We end up with the following geometric interpretation of the two properties of Farey sequences:

  1. If we have rationals a/c > b/d, then C(a,c) \cap C(b,d) is nonempty (and indeed a singleton) if and only if ad-bc = 1. That is, Farey neighbors correspond precisely to tangent pairs of Ford circles. Here, we adopt the convention that fractions are in lowest terms, and negative signs never appear in denominators.
  2. If the Ford circles C(a,c) and C(b,d) are tangent to each other, then the Ford circle C(a+b,c+d) is the unique circle that is tangent to the real line and the other two Ford circles.

The purpose of this post is to point out that these properties (and many more) follow straightforwardly from a natural action of the group SL_2(\mathbb{Z}), which we call \Gamma, on the set of Ford circles. Even though the properties I described are proved with relatively short calculations, I think it doesn’t hurt to have a broader organizing principle in mind.

Recall that \Gamma = SL_2(\mathbb{Z}) is made out of integer matrices \left( \begin{smallmatrix} a & b \\ c & d \end{smallmatrix} \right) satisfying ad-bc = 1. This is a group under matrix multiplication, and it has the notable property that its rows and columns are made out of coprime pairs of integers. It also acts on the complex upper half-plane by Möbius transformations: \left( \begin{smallmatrix} a& b \\ c & d \end{smallmatrix} \right) yields the transformation z \mapsto \frac{az+b}{cz+d}. One has the two distinguished generators T = \left( \begin{smallmatrix} 1 & 1 \\ 0 & 1 \end{smallmatrix} \right), and S = \left( \begin{smallmatrix} 0 & -1 \\ 1 & 0 \end{smallmatrix} \right). That is, any element of \Gamma can be made by composing a word made from these two elements and their inverses. We can say that T acts by Translation z \mapsto z+1, while S Spins the upper half-plane around i by a distorted half-rotation: z \mapsto \frac{-1}{z} (this really is a half-rotation if you use the Cayley transformation to turn the half-plane to a disc).

Claim 1: The set of Ford circles has a transitive action of \Gamma by Möbius transformations. In particular, given a matrix \left( \begin{smallmatrix} a& b \\ c & d \end{smallmatrix} \right) \in \Gamma, the corresponding Möbius transformation takes the infinite Ford circle C(1,0) = \mathbb{R}+ i to the Ford circle C(a,c).

Proof: There are many ways to prove the second sentence, and I will say more general things about transforming circles and lines at the end of this post. Here, it is probably easiest to verify directly: Apply the Möbius transformation to points x + i to get \frac{ax+ai + b}{cx+ci+d}, and check that the resulting points lie in C(a,c). To show that this map from the line (plus the point at infinity) to the circle is a bijection, you can check that the derivative is nonvanishing, and note that image points approach the real axis as |x| becomes large. To prove the first sentence, we note that by Euclid’s algorithm, any coprime pair of integers (a,c) admits a pair (b,d) such that ad-bc = 1. This implies all Ford circles lie in the \Gamma-orbit of C(1,0).
QED

By applying the claim to the transformation S, we find that \left( \begin{smallmatrix} a& b \\ c & d \end{smallmatrix} \right) \in SL_2(\mathbb{Z}) takes C(0,1) to C(b,d). Note that the line C(1,0) is (setwise) stabilized by the infinite group \pm \left( \begin{smallmatrix} 1 & 1 \\ 0 & 1 \end{smallmatrix} \right)^{\mathbb{Z}}, and the other circles are stabilized by conjugates.

In the proof of Claim 1, I gave a direct calculational basis for the fact that Möbius transformations take circles and lines to circles and lines. There are other explanations, for example using elementary inversive geometry, but I would be interested to see a solution that avoids calculation altogether. Another interesting question is: If instead of the direct definition we used, we were to define the Ford circles recursively by demanding that they are tangent to circles with smaller denominator, why should we expect their radii to depend only on the denominators? I only know how to motivate this using the group action.

Claim 2: The action of \Gamma on the set of Ford circles induces an action on the set of ordered pairs C(e,f), C(g,h) of Ford circles, preserving |eh-fg|.

Proof: The vectors (e,f) and (g,h) generate a subgroup of \mathbb{Z} \times \mathbb{Z}, and the corresponding quotient of \mathbb{R}^2 has area equal to the index of the subgroup. We need to show that this area is preserved by the \Gamma action and is equal to |eh-fg| when finite. For the first part, we use the previous claim, where we saw that the action of \Gamma on Ford circles induces an action on the corresponding integer row vectors by right multiplication, and the induced action on \mathbb{R}^2 preserves area. The second part follows from the standard theory of cross-products. QED

Now we can prove the Ford circle versions of the claims:

  1. We wish to show that for a/c \in \mathbb{Q}, the set of coprime integer pairs (h,k) satisfying h/k < a/c and C(a,c) \cap C(h/k) \neq \emptyset is precisely the set of pairs satisfying ak-hc = 1. By radius considerations, all Ford circles tangent to C(1,0) have the form C(n,1) for some integer n, and by Claim 1, there exists \left( \begin{smallmatrix} a& b \\ c & d \end{smallmatrix} \right) \in \Gamma that takes C(1,0) to C(a,c). Therefore, C(h,k) is tangent to C(a,c) if and only if it is the image of some C(n,1) under this transformation. By Claim 2, this holds if and only if |ak-hc|=1. The absolute value sign can be removed, since we have chosen a suitable orientation.
  2. We wish to show that if C(a,c) and C(b,d) are tangent to each other and to the real line, then C(a+b,c+d) is tangent to both of them. Since the conclusion is symmetric with respect to switching the circles and changing signs, we may assume that the corresponding fractions have positive denominator and that a/c > b/d. Then \left( \begin{smallmatrix} a& b \\ c & d \end{smallmatrix} \right) \in \Gamma produces the following maps C(1,0) \mapsto C(a,c), C(0,1) \mapsto C(b,d), C(1,1) \mapsto C(a+b,c+d). The claim then follows from the fact that C(1,1) is tangent to C(1,0) at 1+i and to C(0,1) at \frac{1+i}{2}.

There are several useful corollaries to the use of group symmetry. For example, from the fact that C(1,0) \cap C(0,1) = \{ i \}, we can immediately conclude that if ad-bc = 1, then C(a,c) \cap C(b,d) = \left\{ \frac{ai+b}{ci+d} \right\}. We can also see that if cd \neq 0, then this point of intersection lies on the semicircle whose diameter is the real interval [a/c, b/d], since the semicircle in question is the image of the positive imaginary ray i\mathbb{R}_{>0} under the transformation \left( \begin{smallmatrix} a& b \\ c & d \end{smallmatrix} \right). There is also a connection to continued fractions: Given a real number \alpha, we can decree that a rational number a/c is a good approximation of \alpha if |\alpha - a/c| \leq \frac{1}{2c^2}. The set of good rational approximations to \alpha corresponds to the set of Ford circles C(a,c) that intersect the line \alpha + i\mathbb{R} nontrivially. The sequence of circles hit by the line as one approaches the \mathbb{R} from above correspond precisely to the convergents of the signed continued fraction expansion of \alpha. The signed continued fraction expansion of a convergent a/c yields its expansion in terms of the generators S, T \in \Gamma.

13 thoughts on “Farey fractions, Ford circles, and SL_2.”

  2. Thank you for pointing out the Stern-Brocot tree. I had ignored it mostly because I couldn’t think of a good way to fit it in to the discussion of symmetry. Although it has a lot of nice structure, it is missing the group action that you see with Ford circles.

    If you take the orbit of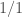 1/1 under the action of the free submonoid of 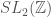SL_2(\mathbb{Z}) generated by \binom{11}{01} and \binom{10}{11}, you produce all of the positive rationals, but the structure you get from left-multiplication is the Calkin-Wilf tree. 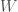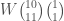In order to get the Stern-Brocot tree, you may use the same monoid, but you have to describe the action by a kind of insertion: Given a word W in the monoid, the corresponding tree element is the rational corresponding to the vector W\binom{1}{1}, and the descendents are W\binom{11}{01}\binom{1}{1} and W \binom{10}{11}\binom{1}{1}. The distinction is essentially the monoid version of right versus left actions of groups on Cayley graphs (or perhaps, Cayley graphs of opposite groups).

    For the Stern-Brocot tree, the right-multiplication of a generator corresponds to adding 1 to the end of an unsigned continued fraction expansion of an entry. For Ford circles, one may also right-multiply words in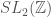 SL_2(\mathbb{Z}) by generators, but this corresponds to operations on signed continued fractions.

  9. Nice post! One small comment, to make matrices in line look smaller you can try using the “smallmatrix” command. For example, \left(\begin{smallmatrix}1 & 0\\ 1 & 1\end{smallmatrix}\right) produces \left(\begin{smallmatrix}1 & 0\\ 1 & 1\end{smallmatrix}\right).

    I apologize if you were already aware of this.

Comments are closed.