There is a rumor circulating here in Japan, to the effect that S. Mochizuki has proved the ABC conjecture. My understanding is that blogs are for spreading such things.
Apparently, he had predicted some years ago that he would finish a proof in 2012, so I suppose this is an “on-time delivery”. It is certainly no secret that his research program has been aiming at the conjecture for several years.
Our very own Noah Snyder did some original work on the function field version of this conjecture, when he was a high-school student.
Update (Sept 4, 2012): This rumor seems to be true! You can find the four “Inter-universal Teichmuller Theory” papers on the very bottom of his papers page.
Secret Blogging Seminar 
What is the status of the proof of Shapiro, at CUNY, and a few other claims?
My understanding is that Szpiro’s (and not Shapiro…) argument was wrong; I am really curious about this rumour. What is it based on?
Did Mochizuki announce a proof? And which version of the ABC conjecture is that (is it `for any epsilon there is a constant…’ or an explicit constant for a fixed and explicit epsilon..)?
does anybody know what happened with Yuhan Zha’s claimed proof using arakelov geometry?
I wondered what he thinks:
http://mathoverflow.net/questions/852/what-is-inter-universal-geometry
He wrote 2009: “I think that it may take another 10 years or so until there exist sufficiently introductory texts”, so more readable explanations may come in 7 years… but such scribblings as linked to in MO can be quite stimulating at least.
is the preprint available somewhere?
What’s happening to David Speyer’s post “What if primes hated to start with nine?” it looks vanished…
Read the man’s words here: http://www.kurims.kyoto-u.ac.jp/~motizuki/thoughts-english.html
In particular the most recent, but dated, post:
“2012-01-23
・Let me report on my progress in writing up the series of papers on
IUTeich. The task of writing up and making a final check on the
contents of the series of papers is proceeding smoothly, and it
appears that the four papers in the series will come to a total of
about 500 pages. Previously (cf. the entry made on 2009-10-15) I
stated that I hope to finish this project by the summer of 2012;
although it is not clear whether or not I will be able to meet
this summer deadline, I do hope to finish by the latter half of the
year 2012. (Nevertheless, of course, I am not able to guarantee
anything at the present time.)”
@zochongzhi I hit publish by accident before the post was ready. It’s mostly finished now, but I still want to generate some pretty graphs to show how zeroes of the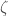
function effect the distribution of primes.
As a total non-expert I’m naturally curious about how this will play out, given the tendency over many generations for people to claim prematurely that they have “proved” some famous old conjecture. Aside from that curiosity, there is the question of how “mainstream” media might try to cover a verified proof. I recall how even a NY Times science writer found it impossible to write down a correct statement of FLT (aside from the more understandable impossibility of explaining to the general public what was actually going on in the work of Wiles, Taylor, and others).
hrd –frm vry srs src– tht thr s n clmd prf.
[Vowels removed by S.C.]
Where can one find the proof?
(Hat tip to Jordan Ellenberg): http://www.kurims.kyoto-u.ac.jp/~motizuki/Inter-universal%20Teichmuller%20Theory%20IV.pdf
Thanks, Richard! It looks very interesting and very difficult.
n th 3rd ppr, p.59, th scnd frml s clrly ncrrct.
[Vowels removed by S.C.]
For the benefit of everyone else, there is no second formula on page 59 of the 3rd paper, unless by ‘formula’ kite meant something other than an equation.
Hopefully, Kite will clarify so experts can examine this purported mistake.
t s mzng hw ppl cn sprd rmrs abt smthng thy cn chck b thmslvs, bt wtht vn chckng… Jst t b clr: thr s n 2nd frml n p.59 f th 3rd ppr. nd t b vn mr clr: th pprch mks lt f sns. nd ths wld nt b th frst tm whn \p_1 tchnqs gv dphntn rslt. Thr s ppr b Km gvng cncrt ncndtnl pplctn f p_1 tchnqs t dphntn gmtry (r-prvng thrm f Sgl).
[Vowels removed by S.C.]