Musings on D-modules

Here in Berkeley, we are having a small learning seminar on D-modules, trying to read Bernstein’s notes. Thursday we had an organizational meeting and on Monday Anton is giving the first talk.

If I had been more organized, I would have given a motivational talk on Thursday trying to explain why D-modules are interesting. Here is what I would have said.

First, just so that we are on the right page, let me explain the basic concepts. The ring D_X is the (sheaf of) ring(s) of algebraic differential operators on a smooth algebraic variety and a D-module is a (sheaf of) module(s) over this ring. For example, we could take X to be the affine line over \mathbb{C}, in which case D_X = \mathbb{C}\langle x, \partial \rangle / \partial x - x \partial = 1. Here \partial is the differential operator d/dx and x is multiplication by x. In general the ring D_X is a kind of universal enveloping algebra of vector fields over functions.

So here are three reasons why D-modules are interesting.

1. They give an algebraic way of studying differential equations. More specifically, systems of linear partial differential equations. In algebraic geometry, we study systems of polynomial equations and the way we do it is to take the ring of polynomials and quotient by the ideal generated by the equations. Similarly, here if we have some linear PDEs, we can quotient the ring D by these equations, to get a D-module. For example, if we want to study the equation f' = f, we would take M := D_X/D_X(\partial - 1) .

Then a solution of our differential equation is just a D-module homomorphism from M to a D-module of functions O . Compare this to points in an algebraic variety. Note that while we are working with algebraic differential operators, any sheaf of smooth functions O is a D-module. So we can study algebraic, analytic, or smooth solutions to our equations.

Anyway, this is the story you always hear. I wonder if anyone actually studies PDEs in this way. I’d be glad to know if someone has a reference or more information.

2. D-modules are an easy case of non-commutative algebraic geometry. Of course the ring D_X is non-commutative, but more interesting is to observe that it has a filtration (by order of the differential operator) such that its associated graded is commutative. For example, in our case of the affine line, when you take associated graded you get rid of the lower order term “1” in the defining relation, so you are just left with x and \partial commuting, and so just a polynomial ring in two variables.

In general, associated graded of D_X is nothing but the ring of functions on the cotangent bundle of X . So D_X is a non-commutative version of the cotangent bundle and in studying D-modules you are doing non-commutative geometry. This has some applications, because if you find a filtration of your module which is compatible with the filtration of D_X , then you can take the associated graded of the module to get a coherent sheaf on the cotangent bundle. This leads to the concept of characteristic variety.

3. D-modules are related to perverse sheaves. Perverse sheaves are a somewhat mysterious abelian subcategory of the derived category of constructible sheaves on X, viewed with the complex topology. In particular, the category of perverse sheaves is an interesting _topological_ invariant of X. The Riemann-Hilbert correspondence gives us an equivalence of categories between the category of regular, holonomic, D-modules and the category of perverse sheaves. A special case of this is the well-known relation between vector bundles with flat connection and representations of the fundamental group. This correspondence gives us a nice way of thinking about perverse sheaves and also shows that the category D-modules is a topological invariant.

14 thoughts on “Musings on D-modules”

  1. 4. D-modules are sheaves with flat connections.

    An O-module F is a D-module if we have a recipe for acting on it with vector fields V which satisfies the following conditions:
    1) {[}a_V,a_f] = a_{[V,f]}
    2) {[}a_V,a_V'] = a_{[V,V']}
    where a indicates the action of functions/vector fields on sections of $F$.

    A recipe for acting with vector fields is a connection if it satisfies equation 1, which is basically the Leibniz rule for differenting the product of a function and a section. A connection is flat if its curvature vanishes, which is exactly what equation 2 says.

    So D-modules are interesting if you think flat connections are interesting, e.g. you are interested in D-branes.

    5. D-modules are in some ways a substitute for transcendental functions. There’s no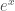 e^x in algebraic geometry, but there is the D-module \mathbb{C}[x,\partial]/(1 - \partial).

  2. 6. D-modules are representations of Lie algebras.

    D is a version of the enveloping algebra of
    vector fields on X, so D-modules are (local versions of) representations of this Lie algebra.
    When a group G acts on a space X, its Lie algebra
    maps to vector fields, and so (global sections of)
    D-modules on X provide a geometric construction of reps of
    the Lie algebra. This leads to Beilinson-Bernstein’s
    theory of localization of representations, one of the most
    powerful tools in rep theory.

    7. D-modules on X are a version of “A-branes” on T^*X.

    There is a (not yet fully understood) close relation
    between D-modules on X and the Fukaya category of T^*X, or more precisely its expanded version involving coisotropic branes — these are D-branes for the A-model of topological strings on the symplectic manifold T^*X. (This comes out of ideas of Kapustin& Witten on the physics side, expanded on mathematically by Nadler and Zaslow)

  3. A side remark: among D-modules there
    are the “smallest” ones (aka holonomic)
    and these are the ones that relate to perverse sheaves/topology, by the Riemann-Hilbert correspondence
    (which sends flat vector bundles to their monodromy).
    Thus as Joel commented the category of [regular holonomic] D-modules is a topological invariant.

    It is however an interesting question to what extent
    the full category of D-modules is a topological invariant.
    Tom Nevins and I showed something like that under
    maps of varieties which are homeomorphisms but are allowed to create cusps. On the other hand I was told recently that Dima Orlov has a result saying something like the statement that you can recover a smooth algebraic variety from the category of (algebraic) D-modules on it [sorry if I’m misquoting, hearsay only!] — so in fact the category of D-modules is the opposite of a topological invariant in some sense.

    [..which is one reason to take with a grain of salt the relation between nonholonomic D-modules and A-branes — one must presume that the topological field theory of Kapsutin-Witten deals with some kind of analytic, not algebraic, D-modules, or some such correction.]

  4. 8. D-modules are related to local cohomologies of sheaves of O-modules. It is actually hard to compute if certain local cohomology vanish or if it’s coherent (most of the time they are not coherent sheaves). D-modules provide the most powerful computational techniques to compute this.

    Also, since you can compute local cohomologies with cech and Kozul complexes, it turns out that local cohomologies of holonomic D-modules are again holonomic. So the connection is more between local cohomologies and “holonomic” D-modules.

  5. so, I realize this is a really old post, but how come, in the first part, you don’t quotient out by like Dx(d/dx – 1)?

  6. Mark – I’m not sure what you mean by the “first part”, but looking at my post again, I see that the D-module related to the equation f’ = f should be D/D(d/dx -1). I don’t know why I put in the x. I’ll fix it.

  7. oh, sorry. came across this post on google. incidentally, it’s one of the top results for “d module of an equation”. trying to learn some of this, mostly interested for the microlocal connection.

  8. Riemann-Hilbert correspondence

    I have seen this phrase in several contexts and I don’t really know what it means. What problem were Riemann and Hilbert solving that led to a correspondence, what corresponds to what, and how has their construction been generalized or strengthened since then?

  9. I don’t really know what Riemann and Hilbert did on the problem, but I can do my best to answer to summarize the correspondence and it’s generalizations.

    The original one correspondence goes:
    Smooth vector bundles on a manifold M with flat connection

    Representations of the fundamental group of M

    Now, to generalize, I’m going to switch to a complex algebraic variety X and algebraic vector bundles with flat connection (to be called flat vector bundles).

    If X is proper:
    Flat vector bundles on X

    Representations of the fundamental group of X

    For X general, this won’t work and Deligne introduced flat vector bundles with regular singularities (RS) — which mean they extend to a vector bundle on \bar(X) with regular singularities.

    RS flat vector bundles on X

    Representations of the fundamental group of X

    Now, let us think of flat vector bundles as D-modules and representations of the fundamental group as locally trivial sheaves of vector spaces on X(C). So we will now generalize as follows — at the same time introducing some categorical language.

    Abelian category of holonomic RS D-modules on X

    Abelian category of perverse sheaves on X

    Derived category of holonomic RS D-modules on X

    Derived category of perverse sheaves on X = Derived category of constructible sheaves on X

    In all cases we have a functor from left to right. This functor can be thought of as looking for “solutions” to the D-module — which generalizes looking for flat section of a flat vector bundle.

    The holonomic property of the D-module means that the corresponding sheaf is constructible. On the other hand the RS property allows us to invert the functor.

  10. Wikipedia’s article speaks a bit to what the Riemann-Hilbert correspondence has to do with Riemann and Hilbert. Basically Hilbert posed a version of the correspondence as his 21st problem and said that it was a problem that Riemann had in mind. See these two articles.

  11. I think the original Riemann-Hilbert problem refers to Hilbert’s 21st problem, asking for existence of linear differential equations having prescribed monodromy on the complex plane. I had been told that Deligne solved it in Springer lecture notes 163, but the wikipedia article seems to indicate that the situation is more complicated. The equivalence of categories that Joel described is due to Mebkhout and Kashiwara.

    There is another problem which falls under the same name, involving contours and factorizations of holomorphic matrix functions. I had seen it used in some work of Connes and Kreimer on perturbative renormalization, but I don’t understand its relation to the original problem.

  13. By the way, there is a precise sense in which a smooth vector bundle with arbitrary connection on a smooth space X is precisely a representation of the path groupoid of X.

    Here by “path groupoid” I mean the groupoid whose objects are the points of X and whose morphisms are thin-homotopy classes of paths in X.

    There is a canonical functor from the path groupoid to the fundamental groupoid of X: the morphisms of the latter are full homotopy classes of paths.

    A vector bundle with connection is flat precisely if, as a representation of the path groupoid, it factors through the fundamental groupoid.

    So flat vector bundles on X are precisely the representations of the fundamental groupoid of X.

    If X is connected, then the fundamental groupoid is equivalent to the fundamental group, regarded as a one-object groupoid.

    This way the theorem that smooth flat vector bundles on connetced spaces are the same as representations of the fundamental group arises as a special case of the theorem which says that smooth vector bundles with arbitrary connection are representations of the path groupoid.

    And this perspective generalizes: smooth 2-vector bundles with connection are 2-representations of the path 2-groupoid.

    And so on.

  14. “An Introduction to Intersection Homology Theory” F. Kirwan 1988 also has a nice introduction to the Riemann-Hilbert problem.

Comments are closed.