Spheres in Higher Dimensions

I just reread this problem on the Harvey Mudd Math Fun Facts website. It’s about your basic intuition in higher dimensions. I remember when I first heard it I was so shocked.

Suppose you have a square in the plane. Cut it into four quadrants, then inscribe a circle in each. Finally add a fifth circle which is just tangent to the other circles.

Square with inscribed circles.

As you can see, it is much smaller then the other circles and the square.

You can repeat this in higher dimensions. For example, you can cut the cube into octants and inscribe eight spheres in these, then add a last final sphere, tangent to the eight inscribed spheres.

So how does the volume of this final sphere change with respect to the volume of the cube when we change dimensions? How does its size compare? It’s always smaller right? WRONG!

As you increase dimension, the final sphere gets bigger and bigger. In dimension 9 it is tangent to the original n-cube and in dimensions bigger than 9 it pushes outside the original cube. Eventually as the dimension increases, the volume of the final sphere exceeds that of the n-cube!

The details are pretty easy and can be found here:
Su, Francis E., et al. “High-Dimensional Spheres in Cubes.” Mudd Math Fun Facts. http://www.math.hmc.edu/funfacts.

There are all sorts of other cool math fun facts on this webpage. You should check it out.

10 thoughts on “Spheres in Higher Dimensions”

  2. This phenomenom also manifests as higher-dimensional lattices which seem like they should be good at sphere packing, but in fact have large holes. In such cases, you can often add a whole additional copy of the lattice translated by some amount. This is particularly interesting since I know a couple really interesting lattices that are made this way.

    First is D_4, the root lattice corresponding to the D_4 Dynkin diagram. To make this lattice, start with the integer points in 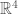\mathbb{R}^4, and think of a sphere of radius 1/2 centered at each lattice point. As you mention above, this is a crappy sphere packing; as a new sphere can fit at any point whose coordinates are all half-integers. Then D_4=\{\mathbb{Z}^4,\mathbb{Z}^4+(1/2,1/2,1/2,1/2)\}. 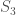I should mention D_4 is interesting because it has an extra S_3 compared it its sibling $late D_n$’s, as you can see from its Dynkin diagram. 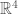This symmetry comes from a quaternionic structure you can put on \mathbb{R}^4.

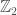    Another nifty lattice you can make this way is the Leech lattice, which is notable both for its excellence at sphere packing and for its relationship to sporadic groups. One starts with the extended Golay code, which is a sublattice in \mathbb{Z}_2^{24} which is excellent at the \mathbb{Z}_2 analog of sphere-packing. This lifts to a lattice in \mathbb{Z}^{24} which is periodic mod 2. This lattice has a LOT of holes in which you can fit spheres… so add another copy of the lifted Golay code translated by (-1/2,-1/2,... -1/2,3/2,-1/2,... -1/2), once for each coordinate. The resulting lattice is the (scaled) Leech lattice… placing a sphere of radius \sqrt{2} at each lattice point gives a packing dense enough that every sphere touches 196,560 neighbors. It also has sporadic symmetry group Co_1, the first Conway group, which contains the first two generations of sporadic groups as subgroups. Hence, 12 of the sporadic groups can be realized as symmetries of the Leech lattice with some structure stabilized.

  3. John,

    Not really, except in the sense that both facts can be proved using asymptotic behavior of the Gamma function. The decreasing volume of the unit ball comes from the superexponential growth of factorials. The growth in volume of the balls here comes from the fact that e times pi is more than eight.

  5. Incidentally, I find the volume question significantly more interesting than the radius question. It is quite rare to find a good geometric application of the size of constants like e.

    The volume of the ball exceeds the volume of the cube when the dimension is at least 1206, and the same goes for the surface area of the boundary when the dimension is at least 2011. These are pretty big for the exponential growth of (e \pi/8)^{dim/2}, but the growth is damped by factor of e^{-\sqrt{dim}} coming from the subtraction in the radius.

    Questions about lattices and sphere packings in high dimension tend to be very difficult and/or boring, because of a sort of phase transition at around dimension 24 or 26 (depending on whether you are a number theorist or a string theorist). We lose the interesting symmetry groups, and sphere packings admit huge tracts of empty space. About 100 years ago, Minkowski gave a nonconstructive lower bound for optimal sphere packing density that still has asymptotics far beyond any known construction.

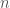  7. Scott: I agree that in dimension 1206 and above the volume of the ball exceeds the volume of the cube – but how does the constant e come in? I’m using the formula V=\frac{2\pi^{n/2}r^n}{n\Gamma(n/2)} for the volume of a sphere in n dimensions with radius r. Are you using Stirling’s approximation for the Gamma function?

  8. Wow, that’s kind of hard to get your head around… intuitively you think that the volume of the sphere certainly can’t be more than the volume of the cube, in any dimension, because how is part of the sphere getting outside the cube? Of course the proof makes sense, but my intuition tends to fail even in three dimensions (because I lack three-dimensional paper).

    One thing that bothers me (and this isn’t a criticism of the hmc.edu page you linked to, but something in general): the usage of “in the ninth dimension” to mean “in R^9”. There’s nothing special about the ninth dimension — it’s only special because the other eight are there too.

  10. Bah, I can’t edit the previous comment. The curse of dimensionality is discussed in those subjects I mentioned but that particular wiki article doesn’t go into the applications specifically. I don’t mean to mislead anyone, I was not really remembering the article that well and didn’t check it til after I had already posted the above.

Comments are closed.