So, I started this series a while back with this post, by talking about some sheaves on an algebraic variety. This post will probably not make a lick of sense to those who haven’t read the first part yet, though you’re welcome to try. The upshot of that was that one has a machine into which one can can feed in
- a variety
defined over
(i.e. defined by polynomials with integer coefficients)
- a choice of stratification of
(a good example might be the orbits of an algebraic group with finitely many orbits, so for example, the Schubert cells on a Grassmannian)
- a set of acceptable local systems valued in your favorite field k (though, if want to do things properly, your favorite field should probably be
).
and receive out the other end a category. The cool fact about this category is that you can think of it as sheaves on the complex variety or its analogue
over characteristic p (let p be your favorite prime) and you will get the same answer. The former category has the advantage of involving geometry that you probably care about, like the cohomology of smooth varieties, and the latter has the advantage that there is a Frobenius acting.
What I’d like to explain in this post how to analyze the structure of this category, and what that has to do with categorification. This will require a bit of machinery, but believe me, the result will justify it.
If you want to categorify things, one thing you’d like to have around is a bunch of categories whose Grothendieck groups you understand. That way, if you’re in the market for a categorification, you know where to browse.
Euler characteristic
Now, what we would like to do is analyze complexes of constructible sheaves by associating functions to them, in a way that gives information about the Grothendieck group. The functions we would really like to use are the Poincaré polynomials (graded dimensions of the cohomology, and I mean as a complex, not sheaf cohomology) of their stalks. This would send, for example, the constant local system to the constant 1 function, which is good. The problem is, this would send every local system to a constant function, which is bad. Even worse, the Poincaré polynomial isn’t an invariant of Grothendieck classes, because there’s a long exact sequence on stalks for each exact sequence in the category of complexes of sheaves. Instead, all you get to keep is the Euler characteristic, which is lovely, but for our purposes pretty weak tea.
However, the Euler characteristic can point us in the right direction. What is it? If one thinks of the dimension of a vector space as the trace of its identity operator, then the Euler characteristic is the supertrace of the homology (the alternating sum of traces; the alternating is necessary to work with long exact sequences). So, if we had a different operator on the stalks that was natural in the sense that it commuted with all long exact sequence differentials, then we would be cooking with gas.
Mixed sheaves
That’s exactly what the Frobenius allows us to get. First of all, we need to consider objects with a bit more structure than just a sheaf. Rather, we need a sheaf that is equivariant for the Frobenius action, that is, with an isomorphism . For any sheaf which is somehow geometrically natural (for example, the constant sheaf for any abelian group), there’s no trouble doing this, though of course, one can always modify this action, say by scalar multiplication.
Now, this Frobenius structure may not seem so exciting, but it is rather important, because it commutes with everything you can possibly imagine. For example, if we have a short exact sequence of complexes of sheaves , then we have a long exact sequence relating the cohomology of these complexes
and all these maps commute with the Frobenius. In particular, if one looks at a point which is fixed by , that is, a point in
, then there is an induced action of the Frobenius on the stalk at this point.
The function-sheaf correspondence
So at each point in , we get a map from the Grothendieck group of our category of sheaves to the base field k, given by the supertrace of
on the stalks. Put another way, for each sheaf
in our category, we get a series of functions
, which only depend on the class of
in the Grothendieck group. Think of this as a map of the Grothendieck group
to the direct sum of functions on
for all n.
I learned this from the book of Kiehl and Weissauer, but it’s much older than that. I’ll leave attribution to the comments.
Theorem. This map is injective.
So, this tells us a lot about the Grothendieck group of our category. But this theorem is most interesting because it’s functorial, in a certain sense. Let denote compactly supported pushforward of sheaves and the naive sum-over-fibers pushforward of functions on finite sets. Similarly, let
denote the obvious pullback of sheaves, and the obvious pullback of functions on open sets.
Theorem. We have equalities ,
and
.
So, lots of geometric operations on sheaves are easy to understand in this picture. Better yet, I’ve talked about the non-equivariant version, but I believe this will work just as well for morphisms between stacks, in which case the points will be a groupoid, not just a set, and the theorem above will say that pull and push on a correspondence is sent to the action of the corresponding span of groupoids on functions (this part, I’m less sure about, though I would be shocked if it wasn’t at least morally right).
This is interesting and I would like to understand it…
What is p and what is q? Also, where is the differential operator on stalks which you were after? Where is the analogue to the Euler characteristic? Is it the supertrace of $Fr^n$ on the stalks? Why are you multiplying the Frobenius by p?
The switch from p to q was an accident.
Also, where is the differential operator on stalks which you were after?
I’m assuming you don’t really mean differential operator. If you mean operator that commutes with differentials, it’s the action of a power of the Frobenius on the stalk at a point fixed by it (a point of ).
).
Where is the analogue to the Euler characteristic? Is it the supertrace of on the stalks?
on the stalks?
Yes, though maybe we don’t have the same Euler characteristic in mind. I have a complex of sheaves, so at each point I have a complex of stalks, and I mean the Euler characteristic of that complex, thought of as a function on your variety. So, if you take the usual cochains, the Euler characteristic at each point is 1 (the Euler characteristic of a small neighborhood of your point).
If you want an analogue of the Euler characteristic of a space, you should take the supertrace of the Frobenius acting on the cohomology of the whole space.
Why are you multiplying the Frobenius by p?
That was a point probably not worth mentioning. I just wanted to emphasize that I could change how the Frobenius acts on my sheaf (not on the underlying variety).
Just to be sure, in your short exact sequence you really want
you really want 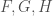 to have
to have  -equivariant differentials, and the maps between them to be
-equivariant differentials, and the maps between them to be  -equivariant. Without the first, there’s no chance that Frobenius acts on the
-equivariant. Without the first, there’s no chance that Frobenius acts on the 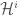 , and without the second also, there’s no chance the maps on
, and without the second also, there’s no chance the maps on 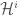 respect Frobenius. (Please correct me if I am mistaken and these are all automatic…)
respect Frobenius. (Please correct me if I am mistaken and these are all automatic…)
Definitely you want everything to have differentials that commute with the Frobenius.
I wouldn’t say that this “automatic” but it is in the “hard to screw up” category of things. The question of exactly how natural these Frobenius structures are is one these that gets rather confusing if you think too hard, but is never a problem in practice. I think if everything is really a sheaf over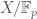 , then there is actually a canonical choice of Frobenius action.
, then there is actually a canonical choice of Frobenius action.
I can’t see anything about multiplication of the Frobenius by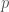 , did this get edited out? I’m wondering, is this the mysterious and secretive Tate twist?
, did this get edited out? I’m wondering, is this the mysterious and secretive Tate twist?
So if I’m extrapolating my buzzwords correctly, I guess that if is a
is a 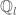 sheaf (or an element of the derived category of), then the notation
sheaf (or an element of the derived category of), then the notation ](https://s0.wp.com/latex.php?latex=%5Cmathcal%7BF%7D%5Bn%5D%28d%29&bg=ffffff&fg=444444&s=0&c=20201002) means to shift
means to shift  in degree by
in degree by 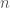 and twist the action of Frobenius by multiplication by
and twist the action of Frobenius by multiplication by  .
.
Knowing something about this twisting would be interesting, for example where it naturally comes up. Though as a non-contributor to the mathematical blogosphere, I can’t really make too forceful a request.
Peter-
Yes, I removed it, since I didn’t actually use it anywhere, and I thought it would just be distracting.
I’m not sure the Tate twist is exactly “secretive.” I mean, it could use a good Wikipedia article (the present one isn’t very clear). For example, you’ve guessed its definition perfectly. It’s really just a book-keeping device to make sure things have the right Galois actions.
Peter — two reasons you might need the Tate twist.
(1) Tate twists occur naturally when dealing with pushforward. For example, let be a family of smooth, irreducible, projective curves. Consider the trivial local system,
be a family of smooth, irreducible, projective curves. Consider the trivial local system,  , on
, on 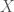 . Every fiber,
. Every fiber,  , has one-dimensional
, has one-dimensional 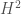 , with canonical generator the form which gives the whole fiber volume
, with canonical generator the form which gives the whole fiber volume 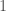 . So you might expect that
. So you might expect that 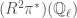 is the trivial local system on
is the trivial local system on 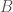 . And that’s correct — except that the Frobenius action is nontrivial. For example, if
. And that’s correct — except that the Frobenius action is nontrivial. For example, if 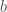 is an
is an 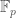 point of
point of 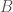 , then the Frobenius is a degree
, then the Frobenius is a degree 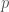 map from
map from  to itself, and hence acts on the top cohomology by multiplication on
to itself, and hence acts on the top cohomology by multiplication on 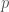 . In general, you can work out that
. In general, you can work out that 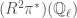 is the first Tate twist of the trivial local system.
is the first Tate twist of the trivial local system.
(2) Another situation where this matters is if you are working with a family defined over and are keeping track of the action of
and are keeping track of the action of 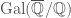 on everything. Then you have different Frobenius actions on the fibers over the different prime numbers. (And, thus, different potential Tate twists.) If you are also doing some nontrivial number theoretic stuff, you need to keep track of Tate twists explicitly in your notation. I’m not the best person to give an example; if commenter Jay is the person I think he is, he probably know some very good ones.
on everything. Then you have different Frobenius actions on the fibers over the different prime numbers. (And, thus, different potential Tate twists.) If you are also doing some nontrivial number theoretic stuff, you need to keep track of Tate twists explicitly in your notation. I’m not the best person to give an example; if commenter Jay is the person I think he is, he probably know some very good ones.
How does one define the compactly supported cohomology of a genuine Artin stack (to make the sheaf-function correspondence work with Artin stacks)? What answer does it give for BG_m?
Regarding Tate twists, I wouldn’t quite describe these as merely book-keeping (perhaps because I am a number theorist).
For example, as a simpler version of the pushforward example in comment 7, if X is P^1 (or in fact any smooth, connected, projective curve) over F_q, then the l-adic cohomology of H^2(X) will not be Q_l, but rather will be Q_l(-1); i.e. a copy of Q_l on which Frobenius acts by q^{-1} (the inverse cyclotomic character).
This is actually very natural: H^2 is generated by a fundamental class. Where does this class come from? Well, thinking topologically, you choose a point x in X, take a disk D around x, and consider the pair (D,D-x). The H^2 of this pair gives the fundamental class. But this is the same as the H^1 of D-x, so H^2 of a smooth projective curve is naturally identified with H^1 of a punctured disk, or if you prefer, with A^1-{0}. (The punctured affine line.) Since H^1 is dual to H_1, we see that H^2 of a curve is dual to H_1 of A^1-{0}.
Now H_1(A^1-{0}) = \pi_1(A^1-{0}), and this we can actually compute concretely. The covers A^1-{0} –> A^1-{0} given by raising to the nth power give all finite covers, and they have deck transformation groups equal to \mu_n (the group of nth roots of unity). Now covering space theory identifies (the profinite completion of) \pi_1 with the inverse limit of these groups of deck transformations, i.e. with the inverse limit of the groups \mu_n.
Now we know how Galois acts on the groups \mu_n: via the cyclotomic character. Thus Galois acts on H^1 of A^1-{0} by the cyclotomic character, and hence on H^2 of our curve X by the inverse cyclotomic character. (A technical remark: if we are working l-adically, we actually restrict n to run over powers of l, but this doesn’t affect anything.)
The above argument is more heursitic than rigorous, the way I’ve written it, but it is in fact a good explanation as to why Tate twists arise in cohomology.
If X is smooth, connected, and projective of dimension d, then its fundamental class looks like the product of d fundamental classes of a curve, and so H^{2d}(X) will be Q_l(-d), the dth power of the inverse cyclotomic character.
Suppose that we want to compute cycle classes. If Z is a codimension i cycle in X (and let me assume is it smooth, just so I can speak about its fundamental class, although this isn’t actually necessary), then the fundamental class of Z transforms by inverse cyclotomic to the d-i, so we get a map
H^{2(d-i)}(X) –> H^{2(d-i)} = Q_l(i-d).
By Poincare duality (and remembering that the fundamental class of X transforms as a -dth Tate twist), we get a map
Q_l(-i) –> H^{2i}(X),
or twisting both sides by i, a map
Q_l –> H^{2i}(X)(i).
(The target is the 2ith cohomology of X, Tate twisted i times.)
The image of this map is the cycle class of Z. It lives in dimension 2i, as you would expect, but not with trivial coefficients, but rather with
coefficients twisted i times.
The moral of this particular story is that Tate twists appear naturally whenever one is thinking about fundamental classes in cohomology over non-algebraically closed fields.
(Another well-known example comes from Tate modules of elliptic curves: it is a well-known fact that the exterior square of the Tate module is equal to the cyclotomic character as a Galois module. Since the Tate module is the H_1 of the elliptic curves, this is just dual to the fact that the exterior square of H^1 of an elliptic curve is canonically H^2 (via the cup product), and Galois acts on H^2 by the inverse cyclotomic character — as a special case of the above discussion.)
Regarding 4, if F is an etale sheaf on X over F_q, then when we base-change to F_q-bar, there are two steps:
First, we base-change X over F_q-bar, to get X-bar; it thus has an action of Gal(F_q-bar/F_q), i.e. of Frobenius. We then pull-back F via the natural map X-bar –> X. Since Frobenius acts as an automorphism of this map (by the first step), the pull-back is thus naturally a Frobenius equivariant sheaf on X-bar. Thus its cohomology over X-bar (which is what one means when one computes the etale cohomology of F, at least in the present dicussion) has a natural action of Frobenius.
All this was totally functorial in the sheaf F, of course, so if we apply it to the members of any diagram of sheaves on X over F_q, then the resulting maps on cohomology will all be Frobenius equivariant.
Short version: the final sentence of Ben’s comment is correct.
David Speyer mentions “canonical generator the form which gives
the whole fiber volume 1.” Basically that’s an orientation. Maybe
it’s intuitive to start with the case of C/R, where you can use
the “usual” topology. Complex curves have natural orientations, but if you
have a curve defined over R, you don’t have complex numberscanonically. The Galois group acts on the numbers and thus the
curve, reversing orientation (think of P^1). People use the
orientation sheaf to deal with non-orientable manifolds, but they
should also use it to deal canonically with orientable manifolds.
Z(1) is the orientation sheaf on a curve and Z(n) on an
n-dimensional variety. The only problem with this analogy is that it degenerates: Z(2)=Z (unless you soup it up with Hodge
structures, etc).
Anyhow: think of the example of a variety defined over R.
Anon- any sheaf on a site has Cech cohomology groups, computed just like they would be for a topological space. Compactly supported cohomplogy is just the dual of the cohomplogy of the Verdier dual. For BG_m, the cohomology is the same as that for the complex points with the usual topology. For compactly supported cohomology, I think you can just use Poincare duality, and the fact the BG_m is -1 dimensional.