Generalized Homology Theories

Recently there have been some comments on our requests page:

Sander Kupers:

Maybe you could explain a bit about elliptic cohomology and topological modular forms…

and Thomas Riepe:

I would be curious about learning more on:
“… many constructions of classical algebra (eg, the theory of modular forms) are beginning to be seen to have deep homotopy-theoretic foundations.”…

Since this is somewhat related to some of my research, I have been recruited volunteered to talk about these things. The problem is that this is a Huge subject and a difficult subject and there is no way to adequately represent it in blog form. On the other hand it is a beautiful subject, filled with lots of exciting tidbits. Why not give it a go anyway, right?

I don’t know about you, but whenever I learn a big subject I find it much easier to understand if it is organized into sensible pieces. I’m going to try to do that on this blog, and the first sensible piece/topic is going to be generalized (co)-homology theories and why we should love them. Really I’m just going to ramble on about them and give some examples. The part about loving them will come later. In fact I won’t even talk about elliptic cohomology or TMF. These are examples of generalized cohomology theories which will come later. 

I’m going to assume that if you’re reading this, you’ve had a semester or two of algebraic topology (or are ambitious enough to teach yourself some of it). If you remember there are probably three things you studied/calculated: homotopy groups, homology, and cohomology. Each of these is a family of functors, one for each integer. The homology/cohomology functors and most of the homotopy functors take values in abelian groups (or the opposite category of abelian groups). A generalized homology theory is going to be the same kind of thing: a functor

Top \to Ab

But before talking about generalized homology let me ask you a question. Why do we like homology better then homotopy? Here’s a hint. What are the homology groups of S^2 ? There is a \mathbb{Z} in dimension 2 and the rest are zero (I’m basically going to use reduced homology theories since it makes a few of the things I want to say easier). Okay, how about the homotopy groups of the 2-sphere? No body knows these.

Let’s do another example. Consider \mathbb{C}P^\infty = K(\mathbb{Z}, 2). This is a space where we know all the homotopy groups. It has a \mathbb{Z} in dimension 2 and the rest is trivial. This is in some sense the dual of the last example. The 2-sphere has complicated homotopy and easy homology. A K(\mathbb{Z},2) has complicated homology but easy homotopy. This is one manifestation of Eckmann-Hilton Duality.

The point is that while the homology of K(\mathbb{Z}, 2) is more complicated then S^2, it is not that complicated. Homology is computable. You probably had an exercise in your topology class where you compute the homology groups of this space, and with a few tricks it is not even that hard. Many people have it as a qual question (which means it doesn’t take, like, days to calculate).

So now we get to the real meat. Why? Why can we calculate with homology so easily but not homotopy?

The answer of course is that we have the Mayer-Vietoris axiom. Conceptually, what this property says is that if we know that a space is built from smaller pieces, then we can build the homology of the space from the homology of the pieces. Effectively this makes homology computable.

Let’s recall the axioms that the homology functor satisfies: A (reduced) homology functor consists of a functor, H, from the category of (nice) based spaces to the category of Abelian groups such that,

  1. If f: X \to Y is a (weak) homotopy equivalence then H(f) is an isomorphism.
  2. If i: A \to X is a cofibration then, H_q(A) \to H_q(X) \to H_q(X/A) is an exact sequence.
  3. For each integer q, there is a natural isomorphism,H_q(X) \cong H_{q+1}( \Sigma X).
  4. If $X$ is a wedge of a set of (nice) based spaces, then the inclusions X_i \to X induce an isomorphism\sum_i H_q(X_i) \to H_q(X).
  5. H_q(S^0) = \mathbb{Z} if q = 0 and is zero otherwise.

This formulation can be found in May’s A Concise Course in Algebraic Topology. The last axiom is known as the dimension axiom. There is a uniqueness result for such functors. Any functor satisfying these axioms is isomorphic to ordinary homology. A generalized homology theory satisfies all the above axioms except we throw out the dimension axiom (5). That’s it. The exacness axiom (2) and suspension axiom (3) imply the Mayer-Vietoris exact sequence.

 

Now let’s look at some examples. One example you probably know is that we can replace the group \mathbb{Z} with any abelian group G we like. You can even compute it exactly like homology, e.g. take the singular chain complex with G coefficients and then take homology. You have the same uniqueness result, again, but in more general examples of homology theories this uniqueness fails. A theory is not determined by its values on S^0.

Here is a construction which I like very much. It is the above example but with coefficients in a topological Abelian group. Let A be a topological Abelian group, to a (pointed) space M we associate a new space of configurations of points in M labeled by A. Basically we take the spaces

(M^n \setminus \Delta M ) \times A^n

which we think of as n distinct points of M, each with a label from A. Then we glue these spaces together so that, for example, we can have a path consisting of two points (labeled a and b) colliding into each other (with their labels adding to a+b). Here M^n really means we smash together the M’s and we also let labels disappear when they collide the base point, but let’s ignore this for now.

Essentially this is a “functor” which associates to each space M a new space C(M; A). We can get a new functor

HA_q(M) = \pi_q C(M; A)

It turns out this is a homology theory. Basically this is a generalization of the Dold-Thom theorem. See Configuration spaces with partially summable labels and homology theories by K. Shimakawa for a discussion and proof of this and related generalizations. I should also mention some names like Dold, Thom, Segal, and probably many others.

The key observation is that this construction turns cofibrations into (quasi)-fibrations and so when we compose with the homotopy group functor we get long exact sequences. A similar argument gives the suspension axiom.

With this construction the homology of the 0-sphere is now easy to compute,

HA_q(S^0) = \pi_q(A)

So (by the uniqueness results) this includes the previous examples. Unfortunately these theories are not much more exciting then ordinary homology.

 

Another more interesting example is given by K-theory, both real and complex flavors. Here the cohomology version is much easier to describe then the homology version so I will stick with that. For each n (including the negative n!) we can consider the Clifford algebras : Cl_n

We have inclsions Cl_n \to Cl_{n+1} (well, at least there is a canonical isomorphism class of Cl_n–Cl_{n+1} bimodule…). Thus we can look at the Grothendieck group of the category of (finitely generated, graded) Cl_n-modules, modulo those which come from CL_{n+1}-modules. In fact we can do this over a space M. We look at the category of bundles of Cl_n-modules over M.

The resulting quotient Grothendieck group is the n-th K-theory group. A little work shows that this actually is a cohomology theory, which goes by the name KO in the real case and just K in the complex case. These two examples (real and complex) are more interesting then the previous examples. The representation theory of Clifford algebras tells us that real K-theory is 8-periodic and complex K-theory is 2-periodic. Even if you fiddle with them to get rid of the negative groups, they still don’t come from any topological abelian group as above.

Let’s take a closer look at some of these groups. For example what is the zero dimensional group (for a space M)? Well Cl_0 \cong \mathbb{R} and Cl_1 \cong \mathbb{C} where the imaginary i is given an odd grading. Thus a Cl_0-module is just a real graded vector space (graded vector bundle over M), and a Cl_1-module is a complex vector space with a \mathbb{Z} / 2\mathbb{Z}-grading where multiplication by i is an odd automorphism (i.e. a graded vector bundle with an odd endomorphism, squaring to -1). Such vector bundles are all isomorphic to one of the form

V \oplus \pi V

where \pi V means the same vector space, with the opposite grading. The complex structure is given in block form by:

\left( \begin{array}{cc} 0 & 1 \\ -1 & 0 \end{array} \right)

Passing from a Cl_1-module to a Cl_0-module is exactly forgetting this complex structure. So the group KO^0(M) is exactly set of isomorphism classes of real graded vector bundles modulo those of the form V \oplus \pi V. Usually a graded vector bundle W is represented as a formal difference of two (ungraded) vector bundles:

W^{ev} - W^{odd}

So you see we recover the usual explanation of what K-theory (in dimension zero) is supposed to be: formal differences of vector bundles. To be slightly technical, what I’ve described is really unreduced K-theory. You can get the reduced K-theory by mucking around with base points or “stabilizing” with trivial bundles. This isn’t really a big deal so I’ll ignore it (like I’ve been doing with most of the details, anyway). 

 

We can calculate the values of a point ( of S^0 for the reduced theory):

\begin{array}{c| c c c c c c c c} n & 0 & 1 & 2 & 3 & 4 & 5 & 6 & 7 \\ \hline KO^n(pt) & \mathbb{Z} & \mathbb{Z} / 2\mathbb{Z} & \mathbb{Z}/ 2 \mathbb{Z} &0 & \mathbb{Z} & 0 & 0 & 0 \end{array}

And these repeat with order 8. 

 

Okay on to another example of a generalized homology theory. Start with a space M. To M (and n) we associate the following group: it is the set of n-manifolds X, equipped with maps to M, modulo the following equivalence relation:

X_0 \sim X_1 if there exists W with X_0 \sqcup X_1 = \partial W and a map from W to M extending the maps X_i \to M.

 

The group structure is given by disjoint union. This theory is known as unoriented bordism. (It should be called bordism because it is a homology theory. Cobordism should be the cohomology theory). There are lots of variations of this example. An obvious one is where we only use oriented manifolds, or spin manifolds, or framed manifolds. There are many other examples too. This will probably be explained in a future post.

When you first learn about homology or cohomolgy it is kinda confusing. You spend all this time defining and working with singular chains. To be honest it is kinda painful and tricky to prove all the axioms like the product axiom and MV axiom. But for bordism it is more or less straightforward. It also has an immediate geometric interpretation. A cycle in bordism is represented by an actual manifold sitting in your space! (Well at least with a map to your space). 

So why don’t we all switch to using bordism instead of ordinary homology? Well here is a question, what is the value on M=point? These are manifolds with maps to the point modulo bordism. The map to a point is no data, so we can forget it. We need to classify n-manifolds up to bordism for all n! This is a tricky geometric problem. The answer is know in the unoriented case and maybe a handful of other cases.

Okay, while we’re on the topic of theories we can’t compute all of, I want to include one last example: Stable homotopy. We started out talking about how homology is nice because it satisfies Mayer-Viatoris while homotopy is not nice because it doesn’t satisfy Mayer-Vietoris. However if you stabilize, things change. The stable homotopy groups are the colimit, 

\pi_n^{st}(M) = \lim_k [ S^{n+k} , \Sigma^k M]

where \Sigma^k M is the kth (reduced) suspension of M. It turns out this is a homology theory! There cold be a whole blog entry (books actually) just about this cohomology theory. There are a lot of ways in which this homology pops its head up. For example it is related to exotic smooth structures on spheres and it plays a role analogous to the integers in the world of homology theories. It is also a special case of the bordism theories described above. Stable homotopy groups are the same as the (stably) framed bordism groups. These are the same homology theory. Unfortunately we can’t compute the stable homotopy groups \pi_n^{st}(S^0) either. The world would be a lot simpler if we could. 

 

There is a whole world of generalized cohomology theories out there. The above examples are just a biased tip of the iceberg. All of the theories I just described have some sort of geometric interpretation be it via configuration spaces, vector bundles, or bordisms in your space. Some even have geometric-quantum field theory interpretations. There are many many more homology theories out there, but most of them don’t have such a nice geometric description as these, specifically the elliptic cohomology theories and also TMF lack any geometric interpretation. One of the goals of the Stolz-Teichner program is to develop a geometric model for TMF using the machinery of quantum field theory. But this is the topic of a later post. 

 

‘Till next time!

7 thoughts on “Generalized Homology Theories”

  1. Nice overview.

    I’d like to better understand on general grounds which kind of cohomology theories can be realized by cocycles (i.e. geometric representatives) that are higher fiber bundles.

    Integral cohomology is about higher line bundles.

    K-theory is about Clifford module bundles.

    “K-theory of K-theory” is about KV 2-vector bundles.

    The expectation driving BDR and ST is that TMF is somehow about 2-Clifford module bundles, or the like.

    I gather that some guys are busy realizing TMF as coming from 2-Clifford algebras with the free fermion local net playing the role of Cl_1. Not really sure how far this has gotten.

    It seems that once the TMF 2-vector bundles connection has been pinned down, one should be able to guess XYZ in XYZ n-vector bundles. I am wondering what (co)homology theory canditates are known that have any chance at all of appearing here.

    In general, is there a way to look at a (co)homology theory and tell whether it can or cannot come from higher bundle geometric cocycles? I guess that not, because I suppose I would have heard of it by now. But maybe somebody has some comments on this.

  2. @ Urs

    It kinda depends on what exactly you mean by “higher fibre bundle” and what you would except as a cocycle. There is an answer but I don’t think you’ll like it.

    In some sense all cohomology theories have a bundle-like interpretation. In the above post I was trying to avoid the concept of spectra, saving it for later. But if you let me use it, then we can argue by analogy with spaces.

    First suppose we have a map of spaces:

    X \to Y

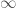    Notice that over Y there is a fibration P_*Y \to Y which is a contractible space over Y. Notice also that the A_\infty-space \Omega Y acts on this space. \Omega Y should be though of as a \infty-categorical analog of a group and this is the classifying bundle. The space Y is then the classifying space. The same sort of analysis as usual then shows that pointed maps from X to Y, up to homotopy, are the same as isomorphism classes of \Omega Y-principal bundles over X.

    More or less the same thing works in the world of spectra too. You then get a bundle of spectra. The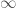 \infty-categorical interpretation should work without problems for connective spectra, but might be problematic for non-connective (e.g. periodic) spectra. In either case it is probably cleanest to restrict to just 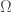\Omega-spectra.

    One problem with this approach is that it is too homotopy theoretic. It is hard to do geometry with these sorts of bundles. Can any sort of index theory be done with just bundles? These questions drive people to look for better interpretations of what a cycle is supposed to be.

    And that’s another thing. There isn’t just one way to represent cocycles for a given cohomology theory. Take K-theory for example. There are almost a dozen different ways to do it.

    I think one of the big goals is to find a sufficiently nice geometric model for TMF which would allow you to actually understand/define some sort of precise index theory on loop space. No one has such a thing.

  3. Chris Said:

    The same sort of analysis as usual then shows that pointed maps from X to Y, up to homotopy, are the same as isomorphism classes of \Omega Y-principal bundles over X.

    Okay Okay this is a lie. If you have a fibration

    \Omega Y \to E \to X

    You have to understand under what conditions it comes via pulling back P_* Y. Here is a paper explaining exactly this.

    So maybe it is not quite as clear cut as I was indicating…

  4. You didn’t sing the KO song!

    (to the tune of “Twinkle Twinkle Little Star”)
    zee two zee two zero zee
    zero zero zero zee
    (repeat infinitely many times)

    Notes: “zed” also works, but “zee mod two zee” doesn’t seem to scan. Does anyone know who came up with this? Mike Hopkins certainly seems to be the most enthusiastic proselytizer.

  5. Dear Chris;
    Nice attempt to give an overview of a gigantic field whose sheer size can be overwhelming to the novice just coming out of a basic algebraic topology course. When you say “generalized homology” or “generalized cohomology”-you are really referring to the bulk of the advances in topology over the last 50 years. Part of the problem for newcomers-both in mathematics and physics-is the fact that the standard textbooks in algebraic topology have become so antiquated in terms of presenting “the basics” that there is now nearly a quantum leap required to reach the frontiers from such a course. This is a hard problem to overcome since the foundations of the subject,despite thier outdatedness to researchers,are large enough that even a strong course cannot cover them all and a mastery of them is required to even COMPREHEND the newer theory let alone master it.May’s book is the only one of the introductions that even tries to bridge the gap-in that regard,its’ an important book and needs to made available to anyone interested in topology.
    But by necessity, May’s book is forced to be incredibly concise to fit all this added material and it’ll be rough going for most students. I know I found it rough going despite an excellent teacher in John Terilla. What’s really needed are strong intermediate texts that will help bridge the gap. There’s Whitehead’s Elements of Homotopy Theory, but this is now woefully out of date. Much better for a beginner is Generalized Cohomology by Adira Kono and Dai Tamaki; which provides an excellent overview with complete references of virtually the whole of modern topology of the last 50 years. It doesn’t present a lot of details,but it’s not trying to-its’ purpose to get the students feet wet and to give them direction towards tackling the mountain that is the current literature. That’s really the best place to start.

  6. May’s book is the only one of the introductions that even tries to bridge the gap-in that regard,its’ an important book and needs to made available to anyone interested in topology.

    It’s available in .pdf on his webpage.

Comments are closed.