Toric varieties are among the simplest objects in algebraic geometry, and they are often a test case for general conjectures. One of the great things about them is that you can completely describe a toric variety by combinatorial data. In this post, I want to explain how this works.
The Projective Plane
To begin with, let’s talk about . I’ll drop the
from now on, as we’ll always be thinking over the complex numbers. I’ll write homogenous coordinates on
as
.
To describe in local coordinates, we need three charts:
,
and
; we’ll call these
,
and
. On the chart
, local coordinates are given by
. Similarly, on the chart
, the local coordinates are
.
Now, of course, there are many ways to choose a system of coordinates on a given chart. Sure, is one coordinate system on
, but
is another. In algebraic geometry, we remove dependence on this sort of choice by not specifying a system of coordinates, but specifying the ring they generate instead. In the example of
, this is the polynomial ring
; this ring depends only on the open set
and is denoted
.
In the particular case of , all of these rings have bases of monomials. I’ll draw a picture to indicate which monomials are in
,
and
. That dot which lies in all three cones (inside the dark triangle) is the origin. The dot directly to the above of the origin is
, and the dot directly to the right of the origin is
.

Let’s look at how and
are glued together. Write
for the intersection
. The functions on
form the ring
. We have a diagram
and is the pushout of this diagram.
Whenever we have a map of spaces , we have a corresponding map of rings from the functions on
to the functions on
; this map is simply pullback. So, we have maps of rings
Again, we can draw a picture:

I encourage you all to draw the pictures for all three charts, their pairwise overlaps and the overlap of all three. I won’t draw that picture, because it is a bit cluttered. We can make it more legible by using three tricks: (1) Slide these cones apart onto different regions of the plane, agreeing tacitly that only the shape of the cone, and not its absolute position, matters. (2) Cut off each cone with a circular arc once it gets too far away from the translated origin. (3) Stop drawing the underlying lattice. So here is how I would draw .
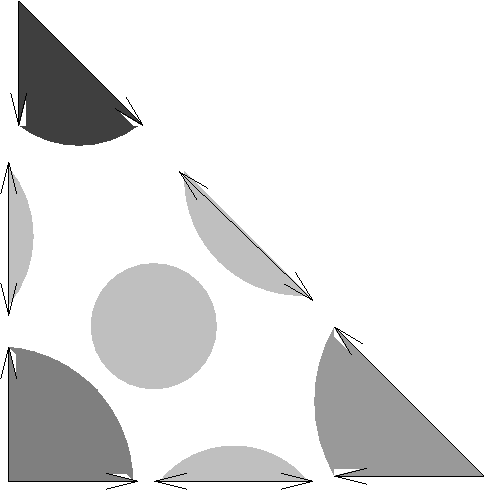
Note that the big blob in the center corresponds to the triple overlap; the corresponding cone is the whole of . Right now, the position of the cones in
is meaningless, but later we will see why I drew them to line up like this.
In general, a toric variety is an algebraic variety that can be described by drawing a bunch of cones like this, where the cones have to obey certain compatibility conditions.
More examples
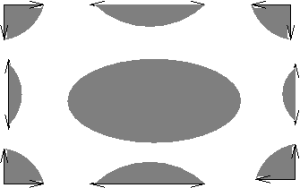 is
is .
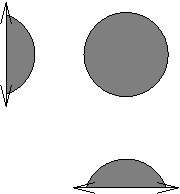 is
is .
 is
is blown up at
.
Constructing a toric variety from a polytope
Stating the compatibility conditions on the cones is a bit technical, so I’ll skip it for now. Instead, I’ll describe a way to get cones that always will obey the required conditions, although not all toric varieties occur in this way.
As you can see, looks like a triangle to me. In general, if we have any polytope
, we can get a collection of cones by the following recipe: There will be one cone for each face
of
. This cone is the set of all vectors of the form
, where
,
and
is a positive scalar. Recall that we allow ourselves to translate cones for ease of drawing; it is usually convenient to draw this cone with the origin in the interior of
. For example, if we start with a rectangle, we get
, above. Again, this doesn’t describe every toric variety (see
above) but it describes a lot of them.
Exercises:
If you are having fun, you might try drawing the following toric varieties. If you’re not having quite that much fine, hopefully this list will convince you that toric varieties provide a fairly versatile class of examples.
(a) ,
and
blown up at
.
(b) The total space of the following line bundles on :
,
and
.
(c) blown up along
;
blown up first along
and then along the proper transform of
.
(d) (A real challenge!) Write coordinates on as
. Blow up this threefold in the folllowing way: In a neighborhood of
, blow up
first, and
second. In a neighborhood of
, blow up
first, and
second. In a neighborhood of
, blow up
first, and
second. The resulting smooth threefold can not be embedded into projective space (of any dimension) and shows some of the limits of our ability to draw things nicely.
Excellent. Now I just have to explain about hypertoric varieties.
I don’t understand the last part, about blowing up. Doesn’t blowing up the line y = t = 0 automatically make it impossible to blow up y = t = 0 again later? Or are you blowing up separately on each affine open and then gluing?
The latter: on each of the affine opens ,
,  and
and 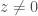 , blow up in the specified order. This is compatible on the overlaps, even though there is no consistent global order of blowing up. Does that make sense, or should I say more?
, blow up in the specified order. This is compatible on the overlaps, even though there is no consistent global order of blowing up. Does that make sense, or should I say more?
Awesome post.
I’m trying to work through it and I’m a bit confused about what the coordinates mean. My guess is that the point (a,b) is supposed to represent the monomial . But this doesn’t seem to quite work with your drawing. For U_y this would mean the cone generated by (0,-1) and (1,-1), but you seem to be drawing the cone generated by (-1,0) and (-1,1). Ok, so clearly I have the coordinates backwards… But then I won’t agree with your statement about x/z being the point to the right of the origin. I assume you’ve just made a typo somewhere? Or am I missing something.
. But this doesn’t seem to quite work with your drawing. For U_y this would mean the cone generated by (0,-1) and (1,-1), but you seem to be drawing the cone generated by (-1,0) and (-1,1). Ok, so clearly I have the coordinates backwards… But then I won’t agree with your statement about x/z being the point to the right of the origin. I assume you’ve just made a typo somewhere? Or am I missing something.
Indeed, I had a thinko. Somewhere between writing the text of this post and drawing the pictures, I switched the meaning of the two coordinates. As of now, the conventions should be that the point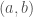 means
means  . That’s not the cleanest fix, but it is a lot easier than redoing all the drawings.
. That’s not the cleanest fix, but it is a lot easier than redoing all the drawings.
Nice post!
I came up with similar diagrams while studying certain generalizations of toric varieties that can be defined over the field with one element. In our diagrams, though, we needed to keep track of the dimensions of each of these cones and blobs, for instance the F_un model of the projective plane consists on a triangle (as in your diagram).
I am a bit confused about what you say concerning polytopes. Do you always get a toric variety with them? We have a similar diagram associated to the Grassmannians. For instance, for Gr(2,4), which is not toric we have something containing 35 cells (6 0-dim, 12 1-dim, 11 2-dim, 5 3-dim and one 4-dim) obviously we didn’t try to draw it, but according to what you say it would look that our diagram would fail to be a polytope…
Yes, every polytope gives a toric variety.
Your description of the Grassmannian is interesting. There is, of course, a torus which acts on the Grassmannian. (If you think of G(2,4) as 2-planes in 4-space, it acs by rescaling the coordinates of 4-space.) This torus action has
6 0-dimensional orbits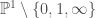 ) 3-dimensional orbits
) 3-dimensional orbits
12 1-dimensional orbits
11 2-dimensional orbits
6 + (
0 4-dimensional orbits
Here, what I mean is that there are 6 exceptional three dimensional orbits — where the six Plucker coordinates vanish — and the other three dimensional orbits lie in a one dimensional family, indexed by the points of . In particular, over a finite field, there are
. In particular, over a finite field, there are 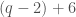 three dimensional orbits.
three dimensional orbits.
It seems that what you have done is figured out a way to convert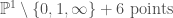 into
into  . Obviously, this gives the right point counts. (Or, to say it in a sophisticated way that means essentially the same thing, they are motivically equal.) What else does your construction give you?
. Obviously, this gives the right point counts. (Or, to say it in a sophisticated way that means essentially the same thing, they are motivically equal.) What else does your construction give you?
Our construction consists basically on decomposing a given variety as “union” (in a technical sense) of tori. These tori do not need to come from a torus action (though if there is a nice torus action the orbits provide the cells).
Once obtained, the decomposition (we call it “torification”) provides a gadget (in the sense of Connes-Consani, though with minor modifications you can get one in the sense of Soulé) over F_1. Different decompositions may provide nonisomorphic gadgets, but they all extend to the same variety over the integers when applying base extension.
In the case of Gr(2,4) the construction is based on the Schubert cell decomposition. Every affine space is decomposed in tori by removing coordinate subspaces (the origin is the 0-dim cell, the axes without the origing the 1-dim cells and so on), and applying this to each of the Schubert cells you get the right counting function.
Not sure if this will have any interest on usual algebraic geometry, beyond the F_1 aspect.
Here’s my favorite example of a complete but nonprojective toric variety.
Write the octahedron as (oct \ southern vertex S) union (oct \ northern vertex N), glued together along a neighborhood of the equatorial square. (The octahedron TV itself is a torus orbit closure in Gr(2,4).)
Now replace the vertex N by an interval, >–<. Geometrically, this blows up the singular point to a P^1. It also requires that one stretch the equatorial square to a non-square rectangle.
But don’t blow up S. So the equator on the southern patch is still a square. That means we can’t glue these back together to make a polytope.
We can nonetheless glue the corresponding toric varieties, as we haven’t changed the open set we were gluing them along.
For those people who prefer fans (usually because, unfortunately, Fulton’s book proceeds that way), the original fan is the cone on the faces of a cube, and we’re subdividing a maximal cone (on a square) into two cones (on triangles). Then the statement is that any piecewise-linear, convex function on
this subdivided fan must actually be differentiable across the new subdividing face.
The way I like to think about toric varieties (but only projective ones) is like this: You start with a cinfiguration of points (say n of them ) with integral coefficients in
) with integral coefficients in 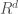 . (You can even assume that no point belongs to the convex hull of the rest.)
. (You can even assume that no point belongs to the convex hull of the rest.)
Next you write down a basis to all affine relations among the points – so if the points affinely span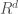 you can consider n-d-1 such affine relations with integral coefficients.
you can consider n-d-1 such affine relations with integral coefficients.
Next you take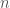 complex variables
complex variables  .
.
Finally you replace every affine relation for the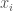 s by a polynomial relation on the
s by a polynomial relation on the 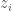 s as in this example:
s as in this example:
Suppose the affine relation is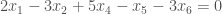
You first write only with positive coefficients
and then translate it into
I do not know if this is a useful way to think about projective toric varieties if you actually want to work with them; but to explain what they are, it is quite simple.
“Yes, every polytope gives a toric variety.”
well not quite, (this may have been obvious from the context); we need a polytope with integral vertices; this is a problem for some applications as there are combinatorial types of polytopes that you cannot realize with vertices of rational coordinates. It is a big mystery how to associate some nice geometric object to non integral/non rational polytopes.
(If you insist on some symmetries some of your favorite famous polytopes are irrational…)
Are all toric varieties (uni)rational?
Alon, yes, all toric varieties are rational. They all contain a subset isomorphic to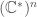 for some n.
for some n.
Gil,
First of all, yes, I should have said that you need the polytope to have lattice points for vertices. If you try to look at a cone like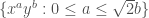 , the corresponding ring is not finitely generated, which causes all sorts of problems.
, the corresponding ring is not finitely generated, which causes all sorts of problems.
As regards the ring you describe, this is basically right, but causes a few issues I will get to in a sec. Here are two alternate descriptions: Algebraically, if is our polytope, let
is our polytope, let  be the cone in
be the cone in  spanned by
spanned by 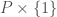 . Take
. Take  , form the corresponding ring and take Proj of that ring. (The grading is by the final coordinate.) That will give you the toric variety for
, form the corresponding ring and take Proj of that ring. (The grading is by the final coordinate.) That will give you the toric variety for  . The construction you describe is the subring generated by the lattice points in
. The construction you describe is the subring generated by the lattice points in  ; this is generally, but not always, the same ring. In particular, your construction can give something non-normal, where as mine will always give a normal variety. Of course, your construction is the thing to use if you want to feed the problem to a computer.
; this is generally, but not always, the same ring. In particular, your construction can give something non-normal, where as mine will always give a normal variety. Of course, your construction is the thing to use if you want to feed the problem to a computer.
There is also a geometric construction: let the points of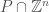 be
be 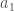 ,
,  , …,
, …, 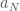 . Here each
. Here each 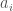 is an integer vector of length
is an integer vector of length 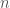 . Map
. Map 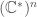 to
to  by
by 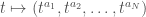 . Here
. Here  and
and  means
means 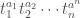 . Take the closure of the image of
. Take the closure of the image of 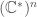 . This closure of Proj of the ring you describe; the normalization of this closure is the toric variety I am describing.
. This closure of Proj of the ring you describe; the normalization of this closure is the toric variety I am describing.
I don’t know how to TeX on this thing. I guess you mean $$ \{ x^a y^b : 0 < a < \sqrt{2} b \} $$ Also, what is a blowup?
Typo fixed, thanks. To produce TeX, type
$ latex \{ x^a y^b : 0 \leq a \leq \sqrt{2} b \}$
but leave out the space between the first dollars sign and “latex”.
Blow ups will take me a little longer, so I’ll get back to that later.
If it helps while david works on something about it, I have a post on blowups <a href=”http://rigtriv.wordpress.com/2008/07/09/blowing-things-up/”here. Parts of it are fairly technical, because I was trying to talk about the most general case that I could, but I work out the example of blowing up a node on an algebraic curve in detail.
Thanks Charles! You’ve got almost excatly the material I’d cover, but in a totally different order. Assuming that I do get around to writing a post on blow ups, it will be interesting to compare them.
This one is just for practice…
Suppose I look at the vectors, e_1, -e_1, e_2, -(e_1+e_2) in R^2, I can compute the kernel of the map from R^4 to R^2 and notice the torus action is:
(u,v). (w_1,w_2,w_3,w_4)—–> ( uv w_1,uw_2,vw_3,uw_4)
But from this how do I see it as CP^2 blown up at one point? Which point is it that is being blown up? It must be a fixed point of the torus action.
From the viewpoint of analysis and PDE it is totally useless to have all this coordinate free stuff, you cannot compute diddly squat anything
esp. the alpha invariants of toric varieties.
“But from this how do I see it as CP^2 blown up at one point? Which point is it that is being blown up? It must be a fixed point of the torus action.”
The (-1) curve is dual to the ray in direction -e_1.
When you say “look at the vectors, e_1, -e_1, e_2, -(e_1+e_2)”, you are describing the toric variety by its fan. So the dual polytope is Hull( (0,1), (1,1), (-1,1), (0,0) ) (a trapezoid). The (-1) curve corresponds to the edge of the trapezoid running from (0,0) to (1,0).
How to see that? I’m not sure what you’ll give me to start with. For example, I could compute the normal bundle. Look at the open neighborhoods of (0,0) and (1,0):![\mathrm{Spec} k[x y^{-1}, y]](https://s0.wp.com/latex.php?latex=%5Cmathrm%7BSpec%7D+k%5Bx+y%5E%7B-1%7D%2C+y%5D&bg=ffffff&fg=444444&s=0&c=20201002) and
and ![\mathrm{Spec} k[x, y^{-1}]](https://s0.wp.com/latex.php?latex=%5Cmathrm%7BSpec%7D+k%5Bx%2C+y%5E%7B-1%7D%5D&bg=ffffff&fg=444444&s=0&c=20201002) . Call those
. Call those ![\mathrm{Spec} k[u_1, v_1]](https://s0.wp.com/latex.php?latex=%5Cmathrm%7BSpec%7D+k%5Bu_1%2C+v_1%5D&bg=ffffff&fg=444444&s=0&c=20201002) and
and ![\mathrm{Spec} k[u_2, v_2]](https://s0.wp.com/latex.php?latex=%5Cmathrm%7BSpec%7D+k%5Bu_2%2C+v_2%5D&bg=ffffff&fg=444444&s=0&c=20201002) , then the gluing is
, then the gluing is  and
and  . That’s the gluing for
. That’s the gluing for 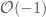 . So the restriction to the neighborhood of this edge is the total space of
. So the restriction to the neighborhood of this edge is the total space of 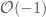 , and this edge is a
, and this edge is a 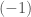 -curve.
-curve.
I don’t know about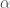 -invariants. Some googling turned up a paper of Song, which might be helpful. Anyone with a better understanding, please post it below.
-invariants. Some googling turned up a paper of Song, which might be helpful. Anyone with a better understanding, please post it below.
Would any one be interested in a 27×27 Magic Square that describes a torus? This arrangement of numbers is perfectly symmetrical as the sum of any pair of numbers equidistant from the center along any axis add up to the order of the square, 27, squared, + 1 which equals 730.