Toric Varieties and Fans

In my previous post, I told you how to create a toric variety from a collection of cones. I also told you that the cones had to satisfy certain, unspecified compatibility conditions. (And that, starting from any lattice polytope, you could build a legitimate collection of cones.)

In this post, I want to tell you what these conditions are. I also want to introduce the way that most experts think about these matters, in terms of fans. For most people, fans are less intuitive than the collections of cones I used in the previous post. But, if you are going to want to think about toric varieties, you should eventually learn how to use the fan language.

So, let’s suppose that we have a finite collection \mathcal{C} of cones in \mathbb{R}^n. (To be careful, you want to assume that each of the cones is rational, a hypothesis which excludes cones like \{ (a,b) : 0 \leq a \leq \sqrt{2} b \}.) If we had any collection of cones at all, each cone would give us a variety. Explicitly, for each cone C, we take the semigroup C \cap \mathbb{Z}^n in \mathbb{Z}^n. This corresponds to a subring of \mathbb{C}[x_1^{\pm}, \ldots, x_n^{\pm}], which we’ll call \mathcal{O}(C). Then we get a variety, U(C), as \mathrm{Spec}(\mathcal{O}(C)).

Gluing the U(C) together would give us something. However, there are two problems: First, the space we get will not be Hausdorff (for those who prefer the language of schemes, will not be separated.) Second, the collection \mathcal{C} will not be recoverable from the scheme we get.

We solve both of these problem by imposing two conditions on the collection \mathcal{C}.

(a) If C is in \mathcal{C}, and v is any vector in C, then C-\mathbb{R}v is also in \mathcal{C}.

(b) If C_1 and C_2 are in \mathcal{C} then there are elements v_1 \in C_1 and v_2 \in C_2 such that C_1+C_2 = C_1 - \mathbb{R} v_1 = C_2 - \mathbb{R} v_2.

Here C - \mathbb{R} v means \{ u-av: \ u \in C,\ a \in \mathbb{R} \} and C_1 + C_2 means \{ c_1+c_2 : \ c_1 \in C_1, \ c_2 \in C_2 \}.

Let’s think about where these conditions come from. In condition (a), suppose that v \in C \cap \mathbb{Z}^n. So x^v is a monomial in \mathcal{O}(C). Then \mathcal{O}(C - \mathbb{R}v) is the localization (x^v)^{-1} \mathcal{O}(C). The translation between rings and varieties tells us that U(C - \mathbb{R} v) is then an open subvariety of U(C). When we glue U(C) into our toric variety, we will also glue in its open subset U(C - \mathbb{R}v). Axiom (a) tells us to include this open subset in our data.

Axiom (b) tells us that we have good patches to glue along. Specifically, it says that the overlap between U(C_1) and U(C_2) is an open subset of each, of the kind discussed in the previous paragraph.

Now, these axioms aren’t that bad. (You might enjoy checking that all the collections of cones in the previous post satisfy them.) But someone (Fulton?) had the brilliant realization that they would look much nicer if we dualized.

Let C be a cone in \mathbb{R}^n. We define the dual cone, C^{\vee} to be \{ v \in \mathbb{R}^n : \langle u,v \rangle \leq 0 \mbox{ for all } u \in C \}. Here \langle \ , \ \rangle is the standard inner product on \mathbb{R}^n. Properly speaking, C and C^{\vee} live in dual vector spaces, but I’m going to ignore that. I should also note that you’ll find different conventions on which sign to use in this definition so, if you need that level of precision, check which convention your source is using.

In our previous post, when we considered \mathbb{P}^2, there were seven cones: \{ a, b \geq 0 \}, \{ a \leq -b \leq 0 \}, \{ b \leq -a\leq 0 \}, \{a \geq 0 \}, \{ b \geq 0 \}, \{ a+b \leq 0 \} and \mathbb{R}^2. The corresponding dual cones are \{ a,b \leq 0 \}, \{ a \geq 0, b \}, \{ b \geq 0, a \}, \{ b=0 \geq a \}, \{ a=0 \geq b \}, \{ a=b \geq 0 \} and \{ a=b=0 \}.

Notice that we can draw all of the dual cones together without overlaps. In fact, I’ve had to slide them apart a little just so you’ll see that there are 7 cones here. I urge you to compare this figure to the third figure in the previous post.

toricfan1

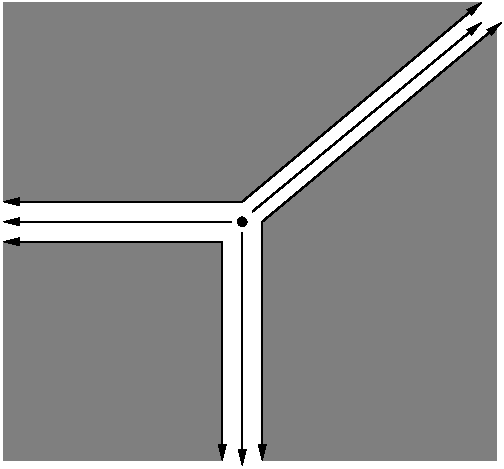
More precisely, the dual cones are a fan. By definition, a fan is a finite collection \mathcal{D} of cones in \mathbb{R}^n obeying two axioms:

(a’) If D is a cone of \mathcal{D}, and F is a face of D, then F is in \mathcal{D}.

(b’) If D_1 and D_2 are cones in \mathcal{D}, then D_1 \cap D_2 is a face of both D_1 and D_2.

These conditions simply arise by translating axioms (a) and (b) into the dual language.

And, finally, I can tell you the definition of a toric variety. A toric variety is a variety built from a fan by (i) dualizing the cones of that fan and (ii) applying the recipe of the previous post.

Let’s have one more example. In the previous post, I drew \mathbb{C}^2 blown up at (0,0). Let’s see how that looks in the fan picture. This time, I haven’t slid the cones apart, but please remember: there are 6 cones in this picture.

toricfan21

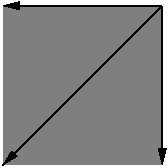
How can we directly see the geometry of the fan from the toric variety? Every toric variety comes equipped with an action of the torus T:=(\mathbb{C}^*)^n. Intuitively, an element (t_1, t_2, \ldots, t_n) of T takes (x_1, x_2, \ldots, x_n) to (t_1 x_1, t_2 x_2, \ldots, t_n x_n). To make that precise, one should describe an action of T on the ring \mathcal{O}(C); I leave that an an exercise for the reader.

Now, each point (a_1, a_2, \ldots, a_n) in \mathbb{Z}^n gives a map \psi_a:\mathbb{C}^* \to T, taking t to (t^{a_1}, t^{a_2}, \ldots, t^{a_n}). Take a generic point x in the toric variety and consider \lim_{t \to \infty} \psi_a(t) \cdot x. This limit exists if and only if a \in \bigcup_{D \in \mathcal{D}} D. Call this limit L_a; then L_a = L_b if and only if a and b lie in the interior of the same cone of \mathcal{D}.

So, the direct meaning of the fan \mathcal{D} is to describe the limiting behavior under the action of the one-parameter subgroups of T.

One could write a book about toric varieties, and people have. Go read them!

Update: The second figure was accidently rotated; it is correct now.

4 thoughts on “Toric Varieties and Fans”

  2. It seems you forgot to give the definition: namely, a toric variety is a normal variety with the action of a torus T, containing an open dense orbit equivariantly isomorphic to T.
    I always get totally confused by the polytopes, and find it much easier to go from the toric variety to the fan than the other way round.
    The books you quote are very good; my favorite remains Tadao Oda’s.

  3. Ah, the standard lecturer’s trick: if you can’t fit something into your lecture, try to get someone to ask you about it during the questions!

    As estraven indicates, there is an intrinsic definition of a toric variety: a normal variety X with an action of a torus $T$, possessing a dense free orbit. (And here variety means seperated, integral and finite type.) From this, it is a theorem that every toric variety comes from a fan. The easy parts of this theorem are the following: every affine toric variety corresponds to a cone, and every open affine subvariety of that toric variety comes from a modifying taking a face of that cone. So, if our toric variety can be covered by open affine toric subvarieties; whose intersections are again open affine toric subvarieties, then our toric variety must come from a fan. The hard part is proving that such a stratification exists!

    As for whether one should go from the toric variety to the fan or the other way around (or to the polytope), that really depends on where your example comes from. If you have constructed a variety in some other way and notice that it has a torus action then yeah, you have the variety and you want to use the construction at the end of my post to make the fan. Varieties that have recently come to me this way are \mathbb{P}^2 blown up at a point, the total space of the tangent bundle to \mathbb{P}^n, the Schubert divisor in G(2,4) and a torus orbit closure in a compactifaction of some Lie group.

    But at least as often, I see toric varieties come up as basic test cases. Someone will want to give an example or a counter-example: to write down a flip, or to describe a tilting sequence and its corresponding quiver, or to give a Gorenstein singularity with no crepant resolution. And, quite often, the simplest example will be toric. If you are using toric varieties this way, then what you need to know is how to decode the fan language, because that is the way the example can be most easily given to you.

  4. I had always wondered what algebraic geometry “is”. Now I have a bunch of examples to compute with: flag varieties, toric varieties, blowups. Gaining facility with these should keep me occupied for some time.

Comments are closed.