You may not know this, but we can see the search terms people use to find our blog. Yesterday, four people came to our blog using the search string “p-adic 2 pi i”. Presumably, people want to know what the -adic analogue of
is.
There isn’t one, and there is a good reason why. I assume that we can all agree that the most important property of is that it is the period of the complex exponential function. Unfortunately, there are no continuous periodic functions on
except for the locally constant functions. The reason is very simple. Suppose that
was periodic with some nonzero period
. Then we would have
for every integer
. But, in the
-adic toplogy, the integers are dense in any neighbourhood of the identity. So
would take the value
infinnitely often near
, and would thus be constant in a neighbourhood of
. The same argument gives that
is constant in a neighborhood of any
. (And the same arguement applies if you take
to be complex valued.)
There is an interesting -analgoue of
, related to the Carlitz exponential. But that is a more complicated, and more interesting, subject.
Judging from our searches, what people want to know today is when Ed Witten’s seminar meets. I’m afraid I don’t know that!
Update: This post has drawn some comments which are far smarter than what I wrote. There is a way to make -adic sense of
, although I don’t understand what it is yet. Come and see our very smart commenters try to explain it to me!
Update: The conversation seems to have stopped for the moment, but I am still trying to understand these period rings, with help from Jay. If I get it, I’ll be sure to post an explanation here.
There is a $p$-adic analogue of $2\pi i$, although for a different definition of $2\p i$; it is also complicated. Here is the basis of the analogy. Consider the variety $X = \mathbb{G}_m$ over $\mathbb{Q}$.
One can attach to $X$ its algebraic de Rham cohomology, whose $H^1$ is a one-dimensional $\mathbb{Q}$-vector space on the canonical basis $dt/t$. (This is a simple algebraic exercise.) Tensoring up to $\mathbb{C}$, Grothendieck’s “algebraic de Rham theorem” shows that one obtains the well-known smooth de Rham cohomology (with complex coefficients) of the complex manifold $X(\mathbb{C})$. (Compare to the fundamental theorem of line integrals, and the residue theorem in complex analysis…)
One can also attach to $X$ the singluar homology of $X(\mathbb{C})$ with coefficients in $\mathbb{Z}$. Since $X(\mathbb{C})$ deformation retracts onto $S^1$, the singular homology is free abelian on one generator; the choice of a square root of $-1$ determines an orientation of $X(\mathbb{C})$ and also a generator $v$ of $H_1$.
The classical (I say: “Archimedean”) de Rham theorem says that “integration” realizes a nondegenerate, $\mathbb{C}$-valued pairing between de Rham $H^1$ and signgular $H_1$. Since these two spaces have rank one, the pairing is determined by the single value $\int_v dt/t$, which, of course, is $2\pi i$. In this sense, $2\pi i$ is be defined to be the “period” of the degree $1$ (co)homology of $X = \mathbb{G}_m$. (Note an internal consistency: $2\pi i$ depends on the choice of $v$, i.e. on a choice of square root of $-1$.)
The $p$-adic analogue of $2\pi i$ comes from knowledge of a non-Archimedean de Rham theorem. It provides a nondegenerate pairing between de Rham $H^1$, which is still generated by $dt/t$, and the $p$-adic etale homology $H_1$, which is a free rank one $\mathbb{Z}_p$-module. Whereas in the singular case $v$ depended on a choice of square root of $-1$, the generator $w$ of the etale homology depends on a choice of compatible system of primitive $p$-power roots of unity. Thus, the $p$-adic $2\pi i$ is the value of $dt/t$ paired with $w$.
A mash of three comments: This sounds straight forward, but didn’t I say earlier that it’s complicated? Wait, you’ve never heard of the non-Archimedean de Rham theorem? In what set did the nondegenerate pairing take its values? Aye, there’s the rub. Something that’s oft-underappreciated by us when we’re young is how arithmetically subtle the topological ring $\mathbb{C}$ is: it is big enough to hold all periods of algebraic varieties. However, $\mathbb{Q}_p$, even $\mathbb{C}_p$ (the $p$-adic completion of an algebraic closure of $\mathbb{Q}_p$), is not big enough! I would love to explain how in more detail, but this comment is already much longer than David’s post.
In short, what Fontaine discovered about 30 years ago is the existence of certain $\mathbb{Q}_p$-algebras, called $B_{crys}^+ \subset B_{dR}^+$, mapping surjectively onto $\mathbb{C}_p$, that do naturally hold all periods of algebraic varieties. This last claim is just a fancy way of saying that the non-Archimedean de Rham theorem pairing, which unfortunately is harder to construct than writing down an integral, takes values in $B_{dR}^+$. (And if a general variety $X$ has good reduction, then the values lie in $B_{crys}^+$.) So the $p$-adic $2\pi i$, whatever it is, is an element of $B_{crys}^+$.
Closing comment: You might quip, “If the $B$-rings surject onto $\mathbb{C}_p$, then why not take the image of $2\pi i$ in $\mathbb{C}_p$?” To this I would reply, its image in $\mathbb{C}_p$ is zero!
But there is a p-adic 2-pi-i. It just doesn’t live on Q_p, it lives on Fontaine’s ring of p-adic periods.
Jay, just last week you were saying you didn’t know anything that would be suitable for discussion on a math blog! If you can write up an understandable explanation of what is, I’d love to see and link to it.
is, I’d love to see and link to it.
I’ll do the easy part, by explaining what Jay is getting at when he talks about “a choice of [a] compatible system of primitive -power roots of unity”. Let’s go back to the archimedean case and think about
-power roots of unity”. Let’s go back to the archimedean case and think about 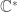 . Consider the path
. Consider the path  which winds once around the puncture in
which winds once around the puncture in 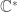 . For any positive integer
. For any positive integer 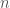 , there is an
, there is an 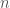 -fold cover of
-fold cover of 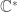 , which I’ll call
, which I’ll call 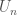 . Monodromy along the path
. Monodromy along the path  gives an automorphism of
gives an automorphism of 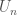 . Explicitly,
. Explicitly,  , with the covering map
, with the covering map  , and the automorphism is of the form
, and the automorphism is of the form  . The
. The 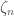 obey certain compatibilities, namely,
obey certain compatibilities, namely,  .
.
Of course, this is all a lot of high-falutin’ language, because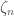 is nothing other then
is nothing other then  .
.
But, if I understand Jay correctly, the -adic analogue of
-adic analogue of  is the data of a choice
is the data of a choice 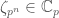 , one such choice for each power of
, one such choice for each power of  , such that
, such that 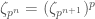 . And, somehow, there is a way to compute a
. And, somehow, there is a way to compute a  -adic analogue of
-adic analogue of  .
.
Jay, thanks for writing that. This question may be ill-posed, but: what are some p-adic varieties with simple periods, if the periods of G_m are already so complicated? For instance you said that the B rings contain Q_p–is it possible to characterize varieties whose periods belong to Q_p? Alternatively, are there other easy-to-describe varieties whose periods vanish in C_p?
Dear dt,
Roughly speaking, zero-dimensional varieties will
have all their periods in Q_p (or finite extensions thereof),
but nothing else will.
As for when the periods vanish in C_p: this is also
pretty common. In the p-adic, as in the classical (archimedean)
setting, there is a Hodge filtration on the de Rham cohomology,
and all the periods which come by “integrating” de Rham
cohomology classes lying in Fil^i for i > 0 will vanish when
pushed down to C_p.
Regards,
Matt
No one said it yet, but the $p$-adic analogue of $2\pi i$ is $\log(\epsilon)$, where $\epsilon$ is the compatible system of $p$-power roots of unity, and where $\log(z)$ is computed using the usual expansion at $z=1$. If you squint, it really does look like the monodromy of the logarithm. Of course, the reason why no one said this is because you have to say what ring you compute the log in and how you view $\epsilon$ as an element of that ring, which takes a bit of work, but I think it’s helpful to say what I did anyway.
Thanks James! Just to head off the obvious, if I take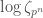 in
in  , the power series will converge, but I get zero. (The baby example of this is
, the power series will converge, but I get zero. (The baby example of this is  in
in  . One can easily check that the power series
. One can easily check that the power series  converges
converges 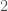 -adically; it’s a lot of fun to compute this sum modulo 8 or 16 and watch it vanish)
-adically; it’s a lot of fun to compute this sum modulo 8 or 16 and watch it vanish)
But there is someplace else that I can take this log and get a nonzero answer? Neato!
You can also form a p-adic Carlitz exponential as a power series (with decent radius of convergence), where the denominators are given by a product over monic polynomials of a given degree in 1/p with Teichmüller coefficients. The set of all such (not necessarily monic) polynomials is rather nice – it is multiplicatively closed, and additively closed mod p. This exponential seems to obey similar functional equations as Carlitz, but I don’t know if it’s useful.
hi, this is my first time commenting on a wordpress blog. i’m a bit scared that there’s no preview button… i hope all my latex works out :-/
anyway i’m just starting to learn this stuff, so i may be making heaps of mistakes, but here’s my take on the -adic rings of periods
-adic rings of periods 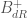 and
and  .
.
before we can define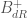 we need to talk a little bit about witt vectors. the usual way we think of a p-adic integer is as an infinite sum
we need to talk a little bit about witt vectors. the usual way we think of a p-adic integer is as an infinite sum 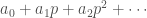 where
where 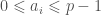 , i.e.,
, i.e., 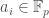 . in other words, our set of digits for
. in other words, our set of digits for  is the set
is the set 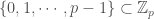 , where we identify this set with elements of
, where we identify this set with elements of  using the inclusion
using the inclusion 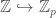 . this is similar to our usual set of base-10 digits for
. this is similar to our usual set of base-10 digits for 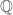 , where write any rational number (say of norm less than 10) as an infinite sum
, where write any rational number (say of norm less than 10) as an infinite sum 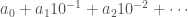 with
with 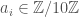 , and where the
, and where the 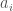 are identified with elements of
are identified with elements of 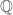 via the inclusion
via the inclusion 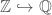 .
.
now this is the only natural way that i can think of to include as a set of digits in
as a set of digits in 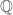 . however there is another very natural way of including
. however there is another very natural way of including 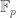 in
in  called the teichmuller map, which works as follows. let
called the teichmuller map, which works as follows. let 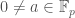 ,
,  . since
. since  for every
for every  , we see that the
, we see that the 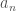 converge to some
converge to some ![[a]\in \mathbb{Z}_p](https://s0.wp.com/latex.php?latex=%5Ba%5D%5Cin+%5Cmathbb%7BZ%7D_p&bg=ffffff&fg=444444&s=0&c=20201002) . (in fact
. (in fact ![[a]](https://s0.wp.com/latex.php?latex=%5Ba%5D&bg=ffffff&fg=444444&s=0&c=20201002) is a
is a  -adic
-adic 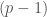 th root of unity.)
th root of unity.) . that is, any
. that is, any  -adic number can be written as a sum
-adic number can be written as a sum ![\sum_{n} p^n [x_n]](https://s0.wp.com/latex.php?latex=%5Csum_%7Bn%7D+p%5En+%5Bx_n%5D&bg=ffffff&fg=444444&s=0&c=20201002) with
with  .
.
we can use these teichmuller representatives as an alternative set of digits for
let be any perfect ring of characteristic
be any perfect ring of characteristic  (perfect means the frobenius map
(perfect means the frobenius map 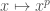 is an automorphism. for example
is an automorphism. for example 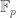 is perfect, but the ring of polynomials
is perfect, but the ring of polynomials ![\mathbb{F}_p[X]](https://s0.wp.com/latex.php?latex=%5Cmathbb%7BF%7D_p%5BX%5D&bg=ffffff&fg=444444&s=0&c=20201002) isn’t.) then there is a unique ring
isn’t.) then there is a unique ring  called the ring of witt vectors, which has characteristic 0, has a unique maximal ideal, and has
called the ring of witt vectors, which has characteristic 0, has a unique maximal ideal, and has  as its residue field. this is a generalization of the
as its residue field. this is a generalization of the  -adic numbers—if
-adic numbers—if 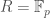 , then
, then  . any ring of witt vectors has a multiplicative teichmuller map
. any ring of witt vectors has a multiplicative teichmuller map ![x\mapsto [x]](https://s0.wp.com/latex.php?latex=x%5Cmapsto+%5Bx%5D&bg=ffffff&fg=444444&s=0&c=20201002) , and just as before, any element
, and just as before, any element  can be written in a unique way as
can be written in a unique way as ![\sum_i [x_i] p^i](https://s0.wp.com/latex.php?latex=%5Csum_i+%5Bx_i%5D+p%5Ei&bg=ffffff&fg=444444&s=0&c=20201002) with the
with the 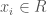 .
.
our ring of periods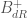 is a completion of a ring of witt vectors. let
is a completion of a ring of witt vectors. let 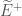 be the set of all sequences
be the set of all sequences  in
in 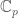 with
with 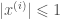 and
and  . we make this into a ring by the rules
. we make this into a ring by the rules  and
and  . you can check that this ring has characteristic
. you can check that this ring has characteristic  , and it’s a perfect ring since everything in
, and it’s a perfect ring since everything in 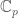 has
has  -th roots. define a valuation on
-th roots. define a valuation on 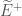 by
by 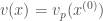 . let
. let ![\widetilde{B}^+ = W(\widetilde{E}^+)[1/p]](https://s0.wp.com/latex.php?latex=%5Cwidetilde%7BB%7D%5E%2B+%3D+W%28%5Cwidetilde%7BE%7D%5E%2B%29%5B1%2Fp%5D&bg=ffffff&fg=444444&s=0&c=20201002) . by the teichmuller map, this is the set of all sums
. by the teichmuller map, this is the set of all sums ![\sum_i [x_i] p^i, x_i\in \widetilde{E}^+](https://s0.wp.com/latex.php?latex=%5Csum_i+%5Bx_i%5D+p%5Ei%2C+x_i%5Cin+%5Cwidetilde%7BE%7D%5E%2B&bg=ffffff&fg=444444&s=0&c=20201002) . define a map
. define a map  by
by ![\sum [x_i] p^i\mapsto\sum x_i^{(0)}p^i](https://s0.wp.com/latex.php?latex=%5Csum+%5Bx_i%5D+p%5Ei%5Cmapsto%5Csum+x_i%5E%7B%280%29%7Dp%5Ei&bg=ffffff&fg=444444&s=0&c=20201002) . let
. let 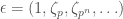 be a compatable system of primitive
be a compatable system of primitive  -th roots of unity like david was talking about before, considered now as an element of
-th roots of unity like david was talking about before, considered now as an element of 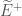 , and let
, and let ![\omega = ([\epsilon]-1)/([\epsilon^{1/p}]-1) = 1 + [\epsilon^{1/p}] + \cdots + [\epsilon^{(p-1)/p}]](https://s0.wp.com/latex.php?latex=%5Comega+%3D+%28%5B%5Cepsilon%5D-1%29%2F%28%5B%5Cepsilon%5E%7B1%2Fp%7D%5D-1%29+%3D+1+%2B+%5B%5Cepsilon%5E%7B1%2Fp%7D%5D+%2B+%5Ccdots+%2B+%5B%5Cepsilon%5E%7B%28p-1%29%2Fp%7D%5D&bg=ffffff&fg=444444&s=0&c=20201002) (you can check this equality using the multiplicative property of the teichmuller map). then
(you can check this equality using the multiplicative property of the teichmuller map). then  , and in fact the kernel of
, and in fact the kernel of 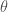 is the ideal generated by
is the ideal generated by 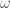 .
.
define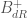 as the completion of
as the completion of  with respect to the
with respect to the  -adic topology. that means every element
-adic topology. that means every element  can be written as a sum
can be written as a sum  with
with  . finally we can construct our `$2\pi i$’ in this ring, as the sum
. finally we can construct our `$2\pi i$’ in this ring, as the sum ![\log ([\epsilon]) := \sum_n (1-[\epsilon])^n/n](https://s0.wp.com/latex.php?latex=%5Clog+%28%5B%5Cepsilon%5D%29+%3A%3D+%5Csum_n+%281-%5B%5Cepsilon%5D%29%5En%2Fn&bg=ffffff&fg=444444&s=0&c=20201002) . in the
. in the  -adic valuation, we have that
-adic valuation, we have that ![v((1-[\epsilon])^n/n) = v(\omega^n\cdot(1-[\epsilon^{1/p}])^n/n) = n](https://s0.wp.com/latex.php?latex=v%28%281-%5B%5Cepsilon%5D%29%5En%2Fn%29+%3D+v%28%5Comega%5En%5Ccdot%281-%5B%5Cepsilon%5E%7B1%2Fp%7D%5D%29%5En%2Fn%29+%3D+n&bg=ffffff&fg=444444&s=0&c=20201002) . since this is strictly increasing as
. since this is strictly increasing as  , this tells us that there won’t be too much `cancellation’ like there was when david tried to take the
, this tells us that there won’t be too much `cancellation’ like there was when david tried to take the  -adic log of
-adic log of  —so our series will converge to something non-zero (of valuation 1).
—so our series will converge to something non-zero (of valuation 1).
ok so it sort of seems like this ring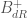 , isn’t really
, isn’t really  -adic anymore. we’ve taken a ring of witt vectors (a `$p$-adic’ thing), and then given it some stupid new topology, just to make our one particular series converge. well this is kind of true. the frobenius automorphism
-adic anymore. we’ve taken a ring of witt vectors (a `$p$-adic’ thing), and then given it some stupid new topology, just to make our one particular series converge. well this is kind of true. the frobenius automorphism 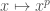 isn’t continous anymore for
isn’t continous anymore for 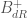 (something that you’d certainly want for a
(something that you’d certainly want for a  -adic object), so you end up having to take a certain subring
-adic object), so you end up having to take a certain subring 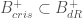 which does have a continuous frobenius.
which does have a continuous frobenius.
but we can see that our![\log ([\epsilon])\in B^+_{dR}](https://s0.wp.com/latex.php?latex=%5Clog+%28%5B%5Cepsilon%5D%29%5Cin+B%5E%2B_%7BdR%7D&bg=ffffff&fg=444444&s=0&c=20201002) is actually a period for something
is actually a period for something  -adic, so it is in fact already a sort of a
-adic, so it is in fact already a sort of a  -adic
-adic  . let
. let  be the cyclotomic character (i.e.,
be the cyclotomic character (i.e.,  for every
for every  -th root of unity). then for any
-th root of unity). then for any  we have
we have ![\sigma(\log([\epsilon])) = \log([\sigma(1,\zeta_p, \ldots)]) = \log([\epsilon^{\chi(\sigma)}]) = \chi(\sigma) \log([\epsilon]).](https://s0.wp.com/latex.php?latex=%5Csigma%28%5Clog%28%5B%5Cepsilon%5D%29%29+%3D+%5Clog%28%5B%5Csigma%281%2C%5Czeta_p%2C+%5Cldots%29%5D%29+%3D+%5Clog%28%5B%5Cepsilon%5E%7B%5Cchi%28%5Csigma%29%7D%5D%29+%3D+%5Cchi%28%5Csigma%29+%5Clog%28%5B%5Cepsilon%5D%29.&bg=ffffff&fg=444444&s=0&c=20201002) (the so-called `ax-sen-tate theorem’ tells us that
(the so-called `ax-sen-tate theorem’ tells us that  doesn’t have any periods in
doesn’t have any periods in  .)
.)
this definition of `period’ might look a bit weird, but you can think of considered as an element of
considered as an element of  as a period for the
as a period for the  -th cyclotomic character
-th cyclotomic character 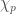 in the same way.
in the same way.
The p-adic numbers Qp don’t have a square root of -1, if p=3 mod 4.
So differentiable functions from Qp[i] -> Qp[i] satisfy the Cauchy-Riemann equations.
To what extent would analysis in Qp[i] have the familiar complex analysis
theorems??? You couldn’t prove that Qp[i] is algebraically complete, I
wonder what would block the complex analysis proof of that, that 1/p(x)
would be a bounded entire function if it had no roots.
Laura