Here’s a neat argument about counting points that you could present at the end of a second course in number theory. I’m sure it’s not original, but, hey, that’s what blogs are for!
Let be a smooth hypersurface in
, over the field
with
elements. The Weil conjectures are conjectures about the number of points of
over
. Specifically, they say that there should be some matrix
such that
and that the eigenvalues of should be algebraic integers of norm
.
Here I am using the Lefschetz hyperplane theorem to know what is for
.
This is, of course, a famously hard theorem. The claim about the eigenvalues is the hardest part, but simply the existence of a matrix for which this formula holds is already quite hard; the first proof was due to Dwork.
What I am going to show you is that there is a much easier proof of the above formula modulo ; a proof of the sort that could be appear in Ireland and Rosen. Many of the terms above disappear mod
, so our goal is just to show that there is some matrix
such that
Some polyhedral notation
Let have degree
. Let
be the simplex
in
. We will use the standard shorthand
to mean the monomial
, for
. For any polytope
, we’ll write
for the lattice points in
.
Let be the defining equation of
, so
is of the form
. Let
.
The rows and columns of will be indexed by the lattice points in the interior of
. We’ll write
for the interior of
.
Remark: I’m going to stick to the case of hypersurfaces in projective space, but this argument generalizes to hypersurfaces in any toric variety, and those of you who are used to toric varieties will recognize that I am choosing my notation accordingly.
The Chevalley-Warning trick
We start with a trick which may be familiar from the proof of the Chevalley-Warning theorem.
Notice that, for a nonnegative integer, we have
.
Let be any polynomial
, where
ranges through some finite subset of
. We deduce that
Let be the hypersurface in affine
space defined by the polynomial
. For
, we have
.
We now compute in two ways and get:
Write
So the above formula is
The second equality is just thinking about which exponents of the form could occur in
.
Finally, we shift from affine space to projective space. We have . So
An example
Let’s look at the polynomial over
. The polytope
is a line segment of length
, so there are two interior lattice points, namely
and
. We have, in part,
(All coefficients are reported modulo .)
So the sum in is
. and we deduce that the number of roots of
in
is
. Sure enough,
has no roots in
.
Similarly,
So, as before, we deduce that the number of roots of in
is also
and, indeed, the polynomial has no roots in that field either.
Finally,
So the number of roots of in
is
and, indeed, all three roots of the polynomial are in this field.
If you compute for higher and higher
values, you’ll see that the coefficients of
and
cycle through
,
and
with period
.
So we are to show that there is some matrix over whose powers have traces
,
and
, repeating cyclically. Certainly, it’s true in this case (a diagonal matrix with entries
and
works). But why is it true in general?
The matrices
Let’s not just look at the coefficients of , for
. Let’s look at the coefficient of
, for
and
. For, example, continuing the previous example, we’ll be looking at the coefficients of
,
,
and
. We’ll organize them into a matrix, with rows indexed by
and columns by
. Call this matrix
.
In the above example, , so
. We also get that
,
, and the values repeat from there. (I highly recommend taking a computer algebra system and having it work out these powers for you. It’s really fun to watch them go!)
It is now obvious what we should prove. We should show that . Then, taking
, we will have
and
, as desired.
Finishing the proof
I feel guilty spelling out the proof. It is so much more fun for you to find it yourselves. Really, once you know what you should be proving, there are only a few reasonable things to try. We adopt the convenient notation for the coefficient of
in the polynomial
.
Okay, here it is. Set . Let
. So we have
. Since the coefficients of our polynomials are in
, we have
, or
.
So, for any and
, we have
We just have to think through what ranges over in this sum.
Well, had better be a lattice point, or there will be no
term in
. Also,
has to be in
, as it is to be an exponent of
. Set
. Then
. So
lies on the interior of the line segment between
, which is in
, and
, which is in
. So
is in
. We conclude that the only nonzero terms in the above sum come from
, and
This is exactly the equation for multiplying matrices. QED.
Some concluding thoughts
I first learned about the Weil conjectures from the introduction to Freitag and Kiehl. This made it seem like an amazing, and thoroughly unmotivated insight, that there should be some cohomology groups around such that the traces of the Frobenius action give the point counts. Looking at examples like this makes the idea seem much more natural. After all, what is the equation but a statement that we have a representation of the group
here? And, in our example, the matrices
repeat with period three — and the Frobenius for the cubic in our above example has order three! Once you see the matrices, it is hard for the modern mind not to look for the group representation.
Of course, this is very anachronistic of me; the modern mathematical mind looks for the group action BECAUSE in part of the success of that method in proving the Weil conjectures. But, to my mind, every bit of demystification helps.
Those who are familiar enough with the theory may be bothered that the size of my matrices is the number of lattice points in the interior of , which is
, not
. This is because the argument I am giving here is the low-tech version of Fulton’s fixed point formula, not of the Lefschetz fixed point formula. Unfortunately, Fulton’s theorem only works modulo
— if you want to count points modulo higher powers of
, you’ll need to work with larger matrices.
Which brings me to a suggestion for someone who really knows this -adic material, and wants to turn out an awesome blog post. It is my vague understanding that Dwork’s great accomplishment was to figure out how to generalize this argument to higher powers of
. If someone wanted to write up how this works to count points modulo
, in the same sort of elementary way, I’d love to read it. UPDATE I have since realized that rationality of the zeta function modulo
is not a good approximation to Dwork’s proof. See comments below.
Dumb question:
Where can I start for pre-requisites to understanding this, haha?
I just finished Group Theory at an undergrad level and I’m starting Real Analysis next semester ._. this post seems like it should be easy to follow from how it’s written, but I’m so outside the field of Algebraic Geometry that I’m not getting anywhere…
My question applies to this blog in general too ;)
You could try reading Ireland and Rosen. Although I didn’t get very far with it when I was at your stage, I nonetheless enjoyed the parts that I did get through.
You meant the Lefschetz hyperplane theorem, not the hard Lefschetz theorem (see e.g. the reference you added!)…
@Florian Thanks!
I have since realized that counting points modulo is less exciting than I thought. Let’s take an example and look at the elliptic curve
is less exciting than I thought. Let’s take an example and look at the elliptic curve  modulo
modulo 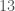 . The coefficient of
. The coefficient of  in
in  is
is 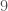 modulo
modulo 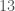 . So the number of points over
. So the number of points over  is congruent to
is congruent to 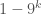 modulo
modulo 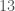 .
.
From the general theory of elliptic curves, the exact point count must be of the form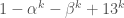 , where
, where 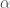 and
and 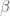 are the roots of a polynomial of the form
are the roots of a polynomial of the form  with
with  . We also know (Riemann hypothesis for elliptic curves) that
. We also know (Riemann hypothesis for elliptic curves) that  , so
, so  . The polynomial
. The polynomial  doesn’t factor over the rationals, but it does
doesn’t factor over the rationals, but it does 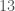 -adically, with roots
-adically, with roots  and
and  . (Here I have written
. (Here I have written 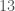 -adic numbers as infinite base
-adic numbers as infinite base 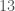 expansions, and
expansions, and  is the digit after
is the digit after 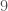 .)
.)
Now, here is what I didn’t realize until this afternoon. For , we have
, we have  . So the point count reduced mod
. So the point count reduced mod  with just be
with just be  , except with a correction factor for the first term.
, except with a correction factor for the first term.
It would still be pretty cool to see a proof similar to the above that the number of points over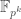 is congruent moduleo
is congruent moduleo  to
to  , with some correction term for
, with some correction term for 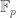 . But it probably wouldn’t give me as much insight into
. But it probably wouldn’t give me as much insight into  -adic cohomology as I thought it would.
-adic cohomology as I thought it would.
A very nice account of Dwork’s argument can be found in
this
memorial article written by Katz and Tate.