Serre has been giving a series of lectures at Harvard for the last month, on finite groups in number theory. It started off with some ideas revolving around Chebotarev density, and recently moved into fusion (meaning conjugacy classes, not monoidal categories) and mod p representations. In between, he gave a neat self-contained talk about small finite groups, which really meant canonical structures on small finite sets.
He started by writing the numbers 2,3,4,5,6,7,8, indicating the sizes of the sets to be discussed, and then he tackled them in order.
There isn’t much to say about a set of size two. It forms a torsor for , and any action of a group on it yields a map
.
If you haven’t seen the word torsor before, it is a fancy way of saying, “the underlying set (or space, etc.) of a group, with the multiplication action.” Baez has an introduction to them, and there is an article on Wikipedia, where it is also given names like heap and “groud”. You can find them in number theory in several guises. For example, if we are given a finite Galois field extension with Galois group
, the field
is a torsor for the group ring
in
-vector spaces (that is, a free module of rank one). Dually, the scheme
is a torsor for the constant group scheme
. I only had one successful research project as an undergrad, and it was a project with Lindsay Childs on classifying objects like these (in particular, fixing the field while varying the Hopf algebra), but I didn’t know that I was doing so at the time.
A set with three elements can be canonically attached to a (2,2) group as the set of nonidentity elements. More geometrically, one can take the hyperplane
of sum zero elements, and there is a canonical map
given by sending an element
, where the zero is in the i-th coordinate. Permutations of this set naturally act by automorphisms on the group.
.
At this point, Serre moved on to four element sets, probably due to some combination of limited time and the fact that that case is much richer. I thought I’d mention a couple other structures, using techniques he mentioned later. One can take rational points on the flag variety, i.e., with
acting by linear fractional transformations, and the identification is the same as above, except instead of a nonzero point, we take the span of it. Alternatively, one can base change to
, and take the six points in the complement of the coordinate planes. These are the nonzero points in the conic
, and their coordinates are permutations of the nonzero elements of
. We can send each element of
to the pair of points whose i-th coordinate is one (or more canonically, fixed under Frobenius).
acts on the six points by permuting the coordinates, and this action preserves the pairs. Switching to characteristic three, we can make the flag
, and for
, take
(or switch “one” with “any nonzero element”). This is a torsor over
, and we can identify an element of
with the unique coordinate that is not equal to any other, since any representative of a point has two equal coordinates. Any identification
induces an isomorphism between the symmetric group and the ax+b group
. There is an analogous multiplicative structure over
given by the “torus flag”
.
acts as a semidirect product of the multiplicative group
with the inversion automorphism (which coincides with the Frobenius in this case). As a final example, the Fermat curve
over the rationals has three rational points, namely those with zero in the i-th coordinate and plus or minus one in the others. It is a genus one curve, so it is a torsor for its Jacobian, an elliptic curve, and it has a canonical action of the semidirect product of its Jacobian with the minus one automorphism, whose group of rational points is isomorphic to
.
A four element set has a structure of an affine space over a (2,2) group. As above, we take the hyperplane
, but this time, there is a line inside:
. The quotient is a (2,2) group
canonically attached to our set, and the three nontrivial elements correspond to the (2,2) partitions. We have a map , and
is a torsor for
, with a permutation action of
by coordinate changes. If we view
as an affine plane, then this action is by affine transformations, and yields an isomorphism
. In ATLAS notation, this is
and
.
Switching to characteristic three, has four points, and linear fractional transformations produce an isomorphism
. We try to make this into something resembling a functor, i.e., the projective line should be canonical. Take the sum-zero hyperplane
, and equip this with the nondegenerate quadratic form
. The zero set of this form defines a conic
with four rational points, and we have an identification of points
, where the zero is in the i-th coordinate. This induces an isomorphism
. More generally, we get a diagram:
where the horizontal arrows are index two inclusions, and the vertical arrows are double cover maps. The central extension is the unique one for which transpositions lift to order two elements, and (2,2) permutations lift to order four elements.
At this point, Serre made a digression to talk about Wiles’ work on the Shimura-Taniyama conjecture. The sequence of ring maps induces a sequence of continuous group homomorphisms
. There is an obstruction in
to the existence of a section. Wiles was able to show that this obstruction vanished for the local Galois representations arising from elliptic curves. In fact, the section factors through
. There is another interesting map
that factors through
, and this has something to do with the fact that thirty one is one more than the Coxeter number of
while three is one more than the Coxeter number of
, but I didn’t hear anything resembling an explanation.
Consider tree made from a central vertex of valence three, three outer vertices of valence three, and six vertices of valence one. What is its automorphism group? To examine it, we take a free rank two module over . The kernel of multiplication by two is a (2,2) group, with three nonidentity elements, which we identify with the outer branches. For each such element, we have two choices of a cyclic subgroup of order four that contains it, and we identify these with the six leaves. This action produces a surjection from
to the automorphism group of this graph, with kernel
. We have
, where the first factor acts by switching all pairs of leaves. Where do we get the set of size four? Take the six leaves, and call them matched if they connect to the same outer branch. There are
ways to split the six leaves into two classes of match representatives. Where does this come up? Take the 4-torsion points on an elliptic curve (over a field of characteristic not two). It is also the Weyl group of
.
Consider a quartic extension of the rationals with symmetric or alternating Galois group. This produces a homomorphism from the absolute Galois group , and we can choose an index three subgroup
and an index two subgroup
. We can take the quotient to get a map
, and this induces a transfer map
. If we set
to be the intersection of conjugates, we have
. We get a tower of fields
, where the first inclusion is cubic, and the second is quadratic, and there is some
such that
. The norm
is rational, and it is a square if and only if the transfer is zero. Godwin has some tables of quartic fields.
Serre didn’t say much about sets of size five. We have . In particular, we get a natural action by automorphisms on
. We also have
, where
is the group of semilinar transformations, i.e., a semidirect product with Galois automorphisms. This also naturally acts on the five points of
by permutations. The action of
is transitive on the six points of
, so it induces a map to
that is a composition of a standard inclusion with an outer automorphism. Unfortunately, Serre didn’t mention any canonical identifications of points like the previous cases, and I couldn’t find one by myself. The presence of semilinear transformations suggests the use of a restriction of scalars, but that doesn’t come out of a nice quadric.
We can view a six point set as the ramified points of the hyperelliptic quotient map from a smooth curve of genus two to . The two-torsion in the Jacobian of the genus two curve is a vector space of rank four over
, and it comes with a natural symplectic form given by the Weil pairing. This provides an isomorphism
.
Switching to characteristic three, we have , where
and
. There is a quadratic form
on the four dimensional space
, which defines a quadric surface in projective three-space. This surface has a rational point, and we can divide such quadrics into those with lines (isomorphic to
) and those without (isomorphic to the Weil restriction
). There is a subgroup of coordinate permutations that induces linear fractional transformations on
, and in fact it realizes
as the index two subgroup
. The odd permutations correspond to semilinear transformations
with square determinant, that is, they incorporate the Galois automorphism. The full group of semilinear transformations is
, which contains
as an index two subgroup, and this property is quite special. For all
, there is a surjection
, but for
, there are outer automorphisms e.g. taking
. One can prove this by enumerating transpositions. The other index two subgroups of
are
and the non-simple Mathieu group
, which is not a split extension.
Serre didn’t say much about sets with seven elements, except to note that had a nontrivial central extension of order three, which is unusual. It can be found by studying the cohomology of the three-Sylow subgroup, and the action of the normalizer. This also works for
, and the central extension is called the Valentine group, which has a three-dimensional complex representation, coming from a map
. It fails for
because it has an embedding of
.
For sets of size eight, we can take spaces as before: , with a nondegenerate quadratic form
on the six-dimensional quotient
. This induces a map
.
has the same Dynkin diagram as
, and indeed,
. How do we see this? Take
. The exterior square
is six-dimensional, and has a split form from the map
. Note that
is a nonisomorphic simple group of the same order.
Serre also pointed out the exceptional isomorphism . One can take the modular curve
, which is genus three, and isomorphic to the Klein quartic. Its automorphism group is
, giving it a 168-fold cover of
. Its Jacobian is three-dimensional, so its two-torsion points form a six-dimensional space over
. This splits into a sum of two 3-dimensional representations under the action of automorphisms, inducing the exceptional isomorphism.
This is great stuff!
I’ve long known one proof that A5 has a transitive action on a 6-element set: A5 is the group of rotational symmetries of a regular dodecahedron, and these act transitively on the dodecahedron’s 6 “axes” (that is, lines between antipodal vertices).
But, recently James Dolan told me another proof: A5 is PSL(2,F5), and the latter group acts transitively on the projective line over F5, which has 6 elements.
He then raised a puzzle: find a natural way to identify the 6 axes of a dodecahedron with the projective line over F5 – where ‘natural’ means that the dodecahedron symmetries act as projective transformations.
Any takers?
I guess you might want me to say what it means to identify the 6 axes of a dodecahedron with the projective line over F5. I’d be happy if you tell me how to compute the cross ratio of any 4 distinct axes.
By the way, if anyone wants to read more about the 168-element group PSL(2,F7) = PGL(3,F2), try week214, week237 and my webpage on Klein’s quartic curve. You’ll even see that the number 168 helps explain the names of the days of the week!
By the way, if anyone wants to read more about canonical structures on small finite sets, see Notes on Finite Geometry.
I’m not sure you’ll like this answer. Exercise three on your “six” page describes coordinates of the 12 vertices of an icosahedron as (1,G,0), together with signs and cyclic permutations, where G=(1+sqrt(5))/2 is the golden ratio. The axes are well-defined on P^2(R), which embeds in P^2(C) which is equivalent to P^2(Q_5^{alg}), and the points are defined on a degree 2 totally ramified extension of Z_5 (in fact, we didn’t need go through the algebraic closure – we could have done the low-brow path through Q(sqrt(5)) to avoid the axiom of choice). We can reduce mod sqrt(5) to get points (1,3,0) with signs and cyclic permutations over F_5. These are the six solutions to x^2+y^2+z^2=0 in P^2(F_5), and they describe a conic P^1.
My mistake – the conic has twelve points, since we have to include the the order-reversing permutations.
am i confused, or were you right the first time? the order-reversing permutations are absorbed by the re-scaling of the solutions, so for example (1,3,0) re-scaled is (3,-1,0) which is the reverse of (0,-1,3). 24 points in the affine variety divided by 4 ways of re-scaling gives 6 points in the projective variety, right?
James,
You’re quite right. I was just thinking that 12 points on a P^1 contradicts the Riemann hypothesis (easy version), but I couldn’t see where I had made a mistake.
I’ve been trying to write down a more real-geometric construction using the Bruhat-Tits building for PGL_3, but it probably ends up being a messy version of the above.
Is there a canonical way to go back from F_5 to the icosahedron?
I might be confused, but how are these maps canonical? For example, to identify a set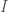 with 3 elements with the subspace of
with 3 elements with the subspace of 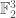 of points whose coordinates sum to 0, one is supposed to define
of points whose coordinates sum to 0, one is supposed to define 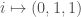 where the 0 is in position i. But to do this you’re picking an isomorphism between
where the 0 is in position i. But to do this you’re picking an isomorphism between 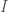 and the set
and the set 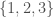 , right? And you’ve also picked a basis for
, right? And you’ve also picked a basis for 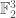 . And once you do this, “canonical” doesn’t seem to mean very much. Am I missing something?
. And once you do this, “canonical” doesn’t seem to mean very much. Am I missing something?
Peter, to mean
to mean  (with basis given by characteristic functions). In the case you mention, we identify an element i with the map from I to
(with basis given by characteristic functions). In the case you mention, we identify an element i with the map from I to 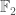 that takes i to zero and the other two elements to one. This doesn’t require a choice of identification of I with
that takes i to zero and the other two elements to one. This doesn’t require a choice of identification of I with  , and it is canonical in the sense that it is equivariant with respect to morphisms in the groupoid of sets with 3 elements. I’m sorry if my notation was confusing.
, and it is canonical in the sense that it is equivariant with respect to morphisms in the groupoid of sets with 3 elements. I’m sorry if my notation was confusing.
When forming a vector space over a field F with a basis given by a set I, one often writes
I’m sure this is well-understood, but for completeness I think it is worth commenting on the functoriality of the isomorphisms of $S_5$ with $P\Gamma L(2,\mathbb{F}_4)$ and $PGL(2,\mathbb{F}_5)$. So suppose $I$ is a 5 element set.
$\mathbb{F}_4$. Consider orderings $\{0,1,2,3,4\}\to I$ and observe that $A_5$ acts on these with two orbits $x,y$. Adjoin $x,y$ to $\mathbb{F}_2$ to make a field of four elements with $x+y=xy=1, x^2=y, y^2=x$. The cross-ratio of four distinct ordered points $x_1,x_2,x_3,x_4\in I$ is now the class of the order $x_0,x_1,x_2,x_3,x_4$ of $I$, where $x_0$ is the fifth point.
This projective line can also be realized as a quadric surface. The representation $H=\{\sum x_i=0\} \subset \mathbb{F}_2^I$ has a quadratic form $\sum_{i<j} x_i x_j$, which defines a nonsingular quadric in $P^3$ over $\mathbb F^2$. This quadric is not ruled, hence has symmetry group $O_4^-(\mathbb{F}_2)$. It may be viewed as the one point compactification of the affine plane over $\mathbb F_2$, by analogy with $\mathbb{C}P^1$ as the one point compactification of $\mathbb{R}^2$.
The action on a six element set can be seen in the Veronese embedding of $P^1$ into $P^2$ over $\mathbb F_4$. This conic is singular and the tangent lines all meet at the singular point (which is not on the conic!). The 21 lines in this plane decompose into 10 chords, 5 tangent lines, and 6 lines which do not meet the conic.
$\mathbb{F}_5$. There are many articles on this, so I will be brief. The construction $L\subset H\subset \mathbb{F}_5^I$ ($L=, H=L^\perp$) yields a 3-dimensional representation $H/L$ with a nondegenerate quadratic form. The points of the corresponding nonsingular conic in $P^2$ are a six element set on which $S_5$ acts.
From this, it is possible to motivate the classical construction of an outer automorphism of $S_6$ by the question: what is a $P^1(\mathbb F_5)$-structure on a six element set? Since the cross-ratio of four distinct points must be -1=4, 1/2 = 3 or 2, any four distinct points are harmonic, so it suffices to distinguish which have cross-ratio -1 (say), i.e., define when a pair $(a,b)$ is harmonically separated by two of the four remaining points. The answer is pleasingly simple: the remaining four points split into two pairs which harmonically separate $(a,b)$ and harmonically separate each other. Thus a $P^1(\mathbb F_5)$ structure distinguishes 15/3 = 5 decompositions of the six points into three pairs such that every pair occurs in precisely one decomposition.
I’m sure this is well-understood, but for completeness I think it is worth commenting on the functoriality of the isomorphisms of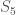 with
with  and
and  . So suppose
. So suppose 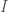 is a 5 element set.
is a 5 element set.
This projective line can also be realized as a quadric surface. The representation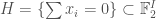 has a quadratic form
has a quadratic form 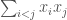 , which defines a nonsingular quadric in
, which defines a nonsingular quadric in 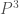 over
over 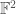 . This quadric is not ruled, hence has symmetry group
. This quadric is not ruled, hence has symmetry group  . It may be viewed as the one point "compactification" of the affine plane over
. It may be viewed as the one point "compactification" of the affine plane over 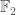 , by analogy with
, by analogy with 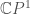 as the one point compactification of
as the one point compactification of 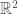 .
.
The action on a six element set can be seen in the Veronese embedding of into
into  over
over 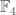 . This conic is singular and the tangent lines all meet at the singular point (which is not on the conic!). The 21 lines in this plane decompose into 10 chords, 5 tangent lines, and 6 lines which do not meet the conic.
. This conic is singular and the tangent lines all meet at the singular point (which is not on the conic!). The 21 lines in this plane decompose into 10 chords, 5 tangent lines, and 6 lines which do not meet the conic.
From this, it is possible to motivate the classical construction of an outer automorphism of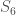 by the question: what is a
by the question: what is a  -structure on a six element set? Since the cross-ratio of four distinct points must be -1=4, 1/2 = 3 or 2, any four distinct points are harmonic, so it suffices to distinguish which have cross-ratio -1 (say), i.e., define when a pair
-structure on a six element set? Since the cross-ratio of four distinct points must be -1=4, 1/2 = 3 or 2, any four distinct points are harmonic, so it suffices to distinguish which have cross-ratio -1 (say), i.e., define when a pair 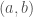 is harmonically separated by two of the four remaining points. The answer is pleasingly simple: the remaining four points split into two pairs which harmonically separate
is harmonically separated by two of the four remaining points. The answer is pleasingly simple: the remaining four points split into two pairs which harmonically separate 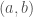 and harmonically separate each other. Thus a
and harmonically separate each other. Thus a  structure distinguishes 15/3 = 5 decompositions of the six points into three pairs such that every pair occurs in precisely one decomposition.
structure distinguishes 15/3 = 5 decompositions of the six points into three pairs such that every pair occurs in precisely one decomposition.