The Outer Automorphism of S_6

I wanted to follow up on a brief comment Scott made in his last post about the outer automorphism of S_6. An outer automorphism is (non-canonically) the same as finding two inequivalent actions of S_6 on 6-element sets.

Consider the set X = \{a, b, c, d, e, f \} with the obvious action of S_6. There are also six points in the projective line \mathbb{P}^1(\mathbb{F}_5). Let’s consider the different ways of turning X into a projective line \mathbb{P}^1(\mathbb{F}_5). There are 6! ways to do this, for example a=0, b=1, c=2, d=3, e=4, f=\infty. But are all these ways really different? The projective line has a lot of automorphisms, so let’s identify two labelings if there is an automorphism of the projective line turning one into the other. Now how many equivalence classes are there? Without loss of generality, since the automorphism group acts 3-transitively we can assume that the labeling has a=0, b=1, and f=\infty. Thus there are only 6 equivalence classes of projective line structures! This is the other action we’re looking for.

I’ll give a quick computation after the cut which shows that this construction is practical for actual computations.

In order to turn the existence of two inequivalent S_6-sets into an outer automorphism of S_6 we pick an identification of the two sets. Say we order the six projective lines as follows:

L_1: a=0, b=1, c=2, d=3, e=4, f=\infty
L_2: a=0, b=1, c=2, d=4, e=3, f=\infty
L_3: a=0, b=1, c=3, d=2, e=4, f=\infty
L_4: a=0, b=1, c=3, d=4, e=2, f=\infty
L_5: a=0, b=1, c=4, d=2, e=3, f=\infty
L_6: a=0, b=1, c=4, d=3, e=2, f=\infty

Now let’s see how the transpostion (1 2) \in S_6 acts on these six lines. It sends L_1 to the line a=1, b=0, c=2, d=3, e=4, f= \infty. Now we need to use an automorphism to put this into the standard form, namely x \mapsto 1-x. This turns the line into a=0, b=1, c=4, d=3, e= 2, f = \infty. So, L_1 is mapped to L_6.

Similar calculations show that L_2 is mapped to L_5; and L_3 is mapped to L_4. Hence under our outer automorphism we have (1 2) \mapsto (1 6)(2 5)(3 4).

Let’s check that this is sensible. An outer automorphism should send any conjugacy class to another conjugacy class of the same order. The number of transpositions in S_6 is 6! / 4! 2! = 15 while the number of products of three disjoint transpositions is 6! / 2! 2! 2! 3! = 15. So we’re ok.

11 thoughts on “The Outer Automorphism of S_6”

  1. IMHO, a more natural description follows from the isomorphism S_6=Sp(4,2). There one identifies the 15 points of the 3-dim projective space over Z/2 with transpositions, and the 15 totally isotropic (w.r.t. the symplectic form) lines with products of 3 disjoint transpositions.

    A yet another possibility is to consider the action of S_6 on the projective plane of order 4. (it stabilises a conic and the intersection point of the tangents to the conic – such a thing is called a “hyperoval”)

    In both cases, appropriate dualities of the projective spaces involved induce outer automorphisms of S_6.
    The Sp(4,2)-interpretation has an advantage of being a generic construction, working for all Sp(4,2^k).

  5. Geordie,
    a group-theoretic answer to why n=6 is so special is that a nontrivial outer automorphism has to map the conjugacy class of transpositions to some other conjugacy class of involutions. But this is only possible when n=6, as easy counting of class sizes tells you.

  6. Dima@1: what the six things that Sp(4,2) permutes? I’ve been wrestling with the symplectic geometry, but I can’t figure it out.

  7. Jeremy-

    I wish I could give a better answer than this, but it seems to be “5-uples of vectors for which all pairwise inner products are non-zero.”

    and the “other” set of 6 points is “5-uples of pairwise disjoint Lagrangian subspaces.”

    The appearance of 5 seems a bit less random when you note that each Lagrangian subspace contains exactly one of your 5 vectors, making this 5-uple an “ovoid.” Similarly, each point in projective space is contained in exactly one of the 5 disjoint Lagrangian subspaces.

    Incidentally, the duality switching lines and Lagrangian subspaces is not vector space duality. The defining representation of a symplectic (or orthogonal) group is always self-dual, so duality does nothing interesting. In fact, I would say that we shouldn’t expect there to be a canonical duality between the two six point sets that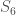 S_6 acts, since there’s no canonical choice of the outer automorphism (there’s a canonical one modulo inner automorphisms, but no way to say which representative is the best).

  8. Ben@7: thanks! I think your remark parallels this fact: given a 6-element set, if we map every point to the set of all pairs that contain it, this map is a bijection between points and pentuples of mutually non-disjoint pairs.

    Also (no disrespect intended) surely it is clear there can’t be a canonical duality between the two S_6-sets: such a canonical map would conjugate one representation to the other, demonstrating that the corresponding automorphism of S_6 was inner, which it ain’t!

  9. Another way of seeing it, implicit in John Baez’s little piece on 6, is to consider the following functors on the category of sets of cardinality 6 and their isomorphisms. Define the contravariant A by
    A(S) = {X subset of S | #X=2}
    the covariant B by
    B(S) = {X subset of A(S) | #X=3, unionX = S}
    and the contravariant C by
    C(S) = {X subset of B(S) | #X=5, unionX = A(S)}.
    I leave it as an exercise to construct natural isos AC -> B, BC -> A and CC-> id. That C is not naturally iso to the identity functor is obvious because it is contravariant. So the
    obvious map j : Iso(S,S) -> Iso(C(S),C(S))
    is an outer automorphism of S_6 that is not
    inner, but jj is.

  10. Jeremy-

    Well, it depends a lot exactly what you mean (I did say “duality” not “bijection”). There are, for example, maps from the set of vectors to the set of Lagrangians and vice versa which preserve the incidence relations, but these maps aren’t equivariant (obviously), so there is a regular action of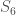 S_6 on the set of such maps.

    But still, point taken. Certainly one shouldn’t expect anything too canonical.

  11. Pingback: Coincidences of tensor categories « Secret Blogging Seminar ~

Comments are closed.