(A guest post by Andrew Sutherland.)
With more than 400 comments tacked on to the previous blog post, it’s past time to rollover to a new one. As just punishment for having contributed more than my fair share of those comments, Scott has asked me to write a guest post summarizing the current state of affairs. This task is made easier by Tao’s recent progress report on the polymath project to sharpen Zhang’s result on bounded gaps between primes. If you haven’t already read the progress report I encourage you to do so, but for the benefit of newcomers who would like to understand how our quest for narrow admissible tuples fits in the bounded prime gaps polymath project, here goes.
The Hardy-Littlewood prime tuples conjecture states that every admissible tuple has infinitely many translates that consist entirely of primes. Here a tuple is simply a set of integers, which we view as an increasing sequence ; we refer to a tuple of size
as a
-tuple. A tuple is admissible if it does not contain a complete set of residues modulo any prime
. For example, 0,2,4 is not an admissible 3-tuple, but both 0,2,6 and 0,4,6 are. A translate of a tuple is obtained by adding a fixed integer to each element; the sequences 5,7,11 and 11,13,17 are the first two translates of 0,2,6 that consist entirely of primes, and we expect that there are infinitely more. Admissibility is clearly a necessary condition for a tuple to have infinitely many translates made up of primes; the conjecture is that it is also sufficient.
Zhang proved a weakened form the prime tuples conjecture, namely, that for all sufficiently large , every admissible
-tuple has infinitely many translates that contain at least 2 primes (as opposed to
). He made this result explicit by showing that one may take
, and then noted the existence of an admissible
-tuple with diameter (difference of largest and smallest elements) less than 70,000,000. Zhang’s
-tuple consists of the first
primes greater than
, which is clearly admissible. As observed by Trudgian, the diameter of this
-tuple is actually less than 60,000,000 (it is precisely 59,874,954).
Further improvements to Zhang’s bound came rapidly, first by finding narrower admissible -tuples, then by optimizing
and the critical parameter
on which it depends (this means making
larger;
is proportional to
). Since it began on June 4, the polymath8 project has been working along three main lines of attack: (1) improving bounds on
and a related parameter
, (2) deriving smaller values of
from a given pair
, and (3) the search for narrow admissible
-tuples.You can see the steady progress that has been made on these three interlocking fronts by viewing the list of world records.
A brief perusal of this list makes it clear that, other than some quick initial advances made by tightening obvious slack in Zhang’s bounds, most of the big gains have come from improving the bounds on (edit: as pointed out by v08ltu below, reducing the dependence of
on
from
to
was also a major advance); see Tao’s progress report and related blog posts for a summary of this work. Once new values of
and
have been established, it is now relatively straight-forward to derive an optimal
(at least within 1 or 2; the introduction of Pintz’s method has streamlined this process). There then remains the task of finding admissible
-tuples that are as narrow as possible; it is this last step that is the subject of this blog post and the two that preceded it. Our goal is to compute
, the smallest possible diameter of an admissible
-tuple, or at least to obtain bounds (particularly upper bounds) that are as tight as we can make them.
A general way to construct a narrow admissible -tuple is to suppose that we first sieve the integers of one residue class modulo each prime
and then choose a set of
survivors, preferably ones that are as close together as possible. In fact, it is usually not necessary to sieve a residue class for every prime
in order to obtain an admissible
-tuple, asymptotically an
bound should suffice. The exact number of residue classes that require sieving depends not only on
, but also on the interval in which one looks for survivors (it could also depend on the order in which one sieves residue classes, but we will ignore this issue).
All of the initial methods we considered involved sieving residue classes 0 mod , and varied only in where to look for the survivors. Zhang takes the first
survivors greater than 1 (after sieving modulo primes up to
), and Morrison’s early optimizations effectively did the same, but with a lower sieving bound. The Hensley-Richards approach instead selects survivors from an interval centered at the origin, and the asymmetric Hensley-Richards optimization shifts this interval slightly (see our wiki page for precise descriptions of each of these approaches, along with benchmark results for particular
values of interest).
But there are sound practical reasons for not always sieving 0 mod . Assuming we believe the prime tuples conjecture (which we do!), we can certainly find an optimally narrow admissible
-tuple somewhere among the primes greater than
, all of which survive sieving 0 modulo primes
. However, the quantitative form of the prime tuples conjecture tells us roughly how far we might need to search in order to find one. The answer is depressingly large: the expected number of translates of any particular admissible
-tuple to be found among the primes
is
thus we may need to search through the primes in an interval of size exponential in
in order to have a good chance of finding even one translate of the
-tuple we seek.
Schinzel suggested that it would be better to sieve 1 mod 2 rather than 0 mod 2, and more generally to sieve 1 mod for all primes up to some intermediate bound and then switch to sieving 0 mod
for the remaining primes. We find that simply following Schinzel’s initial suggestion, works best, and one can see the improvement this yields on the benchmarks page (unlike Schinzel, we don’t restrict ourselves to picking the first
survivors to the right of the origin, we may shift the interval to obtain a better bound).
But sieving a fixed set of residue classes is still too restrictive. In order to find narrower admissible tuples we must relax this constraint and instead consider a greedy approach, where we start by picking an interval in which we hope to find survivors (we know that the size of this interval should be just slightly larger than
), and then run through the primes in order, sieving whichever residue class is least occupied by survivors (we can break ties in any way we like, including at random). Unfortunately a purely greedy approach does not work very well. What works much better is to start with a Schinzel sieve, sieving 1 mod 2 and 0 mod primes up to a bound slightly smaller than
, and then start making greedy choices. Initially the greedy choice will tend to be the residue class 0 mod
, but it will deviate as the primes get larger. For best results the choice of interval is based on the success of the greedy sieving.
This is known as the “greedy-greedy” algorithm, and while it may not have a particularly well chosen name (this is the downside of doing math in a blog comment thread, you tend to throw out the first thing that comes to mind and then get stuck with it), it performs remarkably well. For the values of listed in the benchmarks table, the output of the greedy-greedy algorithm is within 1 percent of the best results known, even for
, where the optimal value is known.
But what about that last 1 percent? Here we switch to local optimizations, taking a good admissible tuple (e.g. one output by the greedy-greedy algorithm) and trying to make it better. There are several methods for doing this, some involve swapping a small set of sieved residue classes for a different set, others shift the tuple by adding elements at one end and deleting them from the other. Another approach is to randomly perturb the tuple by adding additional elements that make it inadmissible and then re-sieving to obtain a new admissible tuple. This can be done in a structured way by using a randomized version of the greedy-greedy algorithm to obtain a similar but slightly different admissible tuple in approximately the same interval, merging it with the reference tuple, and then re-sieving to obtain a new admissible tuple. These operations can all be iterated and interleaved, ideally producing a narrower admissible tuple. But even when this does not happen one often obtains a different admissible tuple with the same diameter, providing another reference tuple against which further local optimizations may be applied.
Recently, improvements in the bounds on brought
below 4507, and we entered a regime where good bounds on
are already known, thanks to prior work by Engelsma. His work was motivated by the second Hardy-Littlewood conjecture, which claims that
for all
, a claim that Hensley and Richards showed is asymptotically incompatible with the prime tuples conjecture (and now generally believed to be false). Engelsma was able to find an admissible 447-tuple with diameter 3158, implying that if the prime tuples conjecture holds then there exists an
(infinitely many in fact) for which
, which is greater than
. In the process of obtaining this result, Engelsma spent several years doing extensive computations, and obtained provably optimal bounds on
for all
, as well as upper bounds on
for
. The quality of these upper bounds is better in some regions than in others (Engelsma naturally focused on the areas that were most directly related to his research), but they are generally quite good, and for
up to about 700 believed to be the best possible.
We have now merged our results with those of Engelsma and placed them in an online database of narrow admissible -tuples that currently holds records for all
up to 5000. The database is also accepts submissions of better admissible tuples, and we invite anyone and everyone to try and improve it. Since it went online a week ago it has processed over 1000 submissions, and currently holds tuples that improve Engelsma’s bounds at 1927 values of
, the smallest of which is 785. As I write this
stands at
(subject to confirmation), which happens to be one of the places where we have made an improvement, yielding a current prime gap bound of 6,712 (but I expect this may drop again soon).
In addition to supporting the polymath prime gaps project, we expect this database will have other applications, including further investigations of the second Hardy-Littlewood conjecture. As can be seen in this chart, not only have we found many examples of admissible -tuples whose diameter
satisfies
, one can view the growth rate of the implied lower bounds on
in this chart.
I would say that improving the k_0 bound from 1/omega^2 to 1/omega^{3/2} [step (2) in your list] was a big gain also, at least back then it was almost a factor of 100. The introduction of the Pintz method has also streamlined the computation process to pass from omega to k_0. Since then it has largely been improving omega.
@v08ltu: Good point, this was an oversight on my part. I’ve made appropriate edits and asked Scott to post them — thanks for the correction.
I’m curious: have you tried a one-step lookahead as a variant of the greedy algorithm? Suppose that the current prime is p_1 and the next is p_2. You could accumulate the number of residues mod p_1, mod p_2, and mod (p_1 p_2) into three arrays A, B, C (of sizes p_1, p_2 and p_1 p_2 respectively of course). From this you could determine which pair of residues (e.g. first mod p_1 and then mod p_2) would minimize the number of elements removed. (E.g. the r_1 and r_2 such that A_r_1 + B_r_2 – C_r_1,r_2 is least.)
You could then actually sieve by the mod p_1 residue and then repeat with p_2 and p_3. This might prevent the greedy step from being too shortsighted?
@Flax: I actually did implement a one-step look-ahead and found that it rarely changed the choices, and that, moreover, the local optimizations were generally able to correct the same sort of mistakes that a one-step look-ahead might avoid. Given that we are running the algorithm in a loop where we iteratively apply random perturbations, I concluded that it made more sense to keep the core component as fast as possible, so that it could process more iterations in a given period of time.
But that’s not to say that a deeper look-ahead might not pay dividends, and I would certainly encourage experimentation along these lines.
There is a trade-off between designing for an algorithm that can fairly quickly get to a good solution versus an algorithm that is willing to burn a lot of time trying to find the best solution possible. Since the polymath8 project started, I don’t think the value of k0 has ever remained stable for more than 4 days at a time, and especially when k0 was much larger than it is now, it was useful to have an algorithm that could quickly get to a good, it not great, solution. This has also been very useful in building the database of admissible tuples for k up to 5000 and being able to quickly populate it with reasonably narrow tuples.
But once things settle down and we have a “final” value for k0, it will be time to buckle down and focus a lot of computation on a particular problem instance (assuming k0 does not drop below 342). I don’t think we’re quite there yet (it looks like k0 could soon drop to around 720). But that doesn’t mean we shouldn’t be thinking about better algorithms now. Another thing worth considering is designing an algorithm that targets a specific diameter, say 2 less then the best value currently known.
A quick update: it looks like we now have a new target k0=720,
http://terrytao.wordpress.com/2013/06/30/bounded-gaps-between-primes-polymath8-a-progress-report/#comment-237489, which gives a prime gap bound of 5414. This bound comes from Engelsma’s original tables and is close to (but not quite in) the region where they are believed to be optimal (but perhaps Thomas can chime in here).
Can someone comment on how difficult it would be to extend the range of provable optimality?
@Pace: Thomas Engelsma is surely the best person to answer this question, but I am running some experiments now that might shed some light on it (the short answer is that I think going beyond k=342 is certainly feasible, but getting to k=720 almost certainly isn’t).
In the mean time, let me note the lower bounds that we do have for H(720). Having fixed a parity issue in my code, I can now confirm all the lower bounds computed by Avishlay using the partitioning method with Engelsma’s bounds for k = 4832.
We can improve this by using one of two additional lower bounds that Engelsma computed. Let k(w) be the largest k for which there exists an admissible k-tuple of diameter strictly less than w. In addition to determining k(w) for all w up to 2329 (where k(2329)=342), Engelsma determined k(2529)=369 and k(2655)=384 (see http://www.opertech.com/primes/k-tuples.html). (NB: these don’t imply H(369)=2528 and H(384)=2654, but they do imply H(370) > 2529 and H(385) > 2655, and also that k(w) <= 384 for all w <= 2655 and k(w) <= 369 for all w <= 2529).
If we partition an interval of width (diameter+1) w=4924 into intervals of width 2269 and 2655, we get
k(4924) 4924, and by parity, H(720) >= 4926.
But this is well short of the upper bound H(720) <= 5414.
WordPress apparently ate part of #7. Tthe end of the second paragraph should say that H(720) >= 4832 follows from a partitioning bound using Engelsma’s optimal bounds for k <= 342. A complete table of such bounds for k = 2330, but we believe H(343)=2340).
Bah, wordpress won’t let me repost the link to Avishlay’s table for some reason, the original post is at https://sbseminar.wordpress.com/2013/06/05/more-narrow-admissible-sets/#comment-24223.
Finally, my last point was that improving lower bounds on H(k) for any k > 342 (or on k(w) for w > 2329) could potentially improve the lower bound for H(720), as well as many others. So an initial goal might be to prove H(343)=2340. We currently only know that H(343) >= 2330.
@Pace: I believe Thomas and Klas should have much more to say on your question. Here are only some thoughts based on my limited experience.
I did implement a recursive depth-first search strategy, constructing from 0 with feasible values and simple pruning based on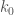 and the current best $H$ value, to do exact computation. In my realization, the performance was highly dependently on the set of residues at small primes (due to the combinatorial nature) that are used by optimal solutions. For example, it needed around 105.2 s to solve
and the current best $H$ value, to do exact computation. In my realization, the performance was highly dependently on the set of residues at small primes (due to the combinatorial nature) that are used by optimal solutions. For example, it needed around 105.2 s to solve 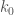 =30, but almost needed no time to solve
=30, but almost needed no time to solve 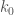 =50. Besides, there might have many optimal solutions for the same
=50. Besides, there might have many optimal solutions for the same 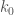 value. (For example, for
value. (For example, for 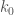 =32, the first, second, and third solutions can be found in 0.0s, 24.23s, and 24.26s.) I believe that the search might be somewhat accelerated (but only for some small
=32, the first, second, and third solutions can be found in 0.0s, 24.23s, and 24.26s.) I believe that the search might be somewhat accelerated (but only for some small 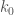 instances) if using some randomness in selecting the next node.
instances) if using some randomness in selecting the next node.
The problem might be tackled much more efficiently if some nice properties about possible optimal substructures can be established, for pruning the search space at very early stages.
BTW: Maybe the discussion about the problem property in the previous blog, e.g., #391, #392, #405, and #406 (by Terence and Andrew), can stimulate more positive clues in the near future.
Last night I ran a program to try and naively assess the feasibility of computing optimal bounds on H(k). Given k and a target upper bound d on H(k), the program attempts to prove that H(k) >= d by sieving the interval [0,d-2] and verifying that you cannot get k survivors (if this verification fails, it outputs an admissible k-tuple of diameter less than d, thereby proving H(k) < d. It assumes (wlog) that 0 is unseived, so for each prime p <= k it checks the residue classes from 1 to p-1 mod p, pruning the search by always requiring the number of survivors to stay above k.
Running overnight on my laptop, the program was able to verify all of Engelsma's lower bounds for k up to 200. The longest computation was for k=198, which took about 1.5 hours and required about 7.5*10^11 sieving operations; it reached a maximum search depth of 24 primes (up to p=89), with an "average" search depth of about 11.5.
The chart below shows a plot of k vs the base-10 log of the # of sieving operations needed to compute a tight lower bound on H(k). A crude back-of-the-envelope argument (see below) suggests that the "feasible" limit of this approach is around 10^20 sieving operations. Depending on how you fit the curve (it's clearly subexponential) this corresponds to k around 400-500. So I think it is definitely feasible to get tight bounds for k well above 342, but 720 is clearly out of reach with this approach (something more clever would be required).
Optimistic back-of-the-envelope calculation that intentionally ignores many technical details: With a straight-forward C implementation, the "average" sieving operation takes about 70-80 nanosecs on my laptop (including the time to update the survivor count), with the interval size around 1000. As k increases the interval size goes up but the cost of sieving goes down (sieving mod bigger primes is faster), so let's call it a wash and suppose the time to sieve one residue class is a constant. One can gain a factor of 2 by taking advantage of symmetry (I didn't), and I'm willing to believe that a careful assembly language implementation that avoids branching inside the critical loops might gain another factor of 5 or 10. So say 5-10 nanosecs per sieving operation on a sequential non-SIMD architecture. It's not unreasonable to suppose we might gain a factor of 500 or even 1000 due to parallelism on a GPU (combination of SIMD and multi-threading). So for the sake of argument let's suppose we can do 10^11 sieving ops/sec/GPU, and that we are willing to throw 100 GPUs at the problem and let them grind away for, say, 10^7 seconds (about 4 months). That gets us 10^20 sieving operations.
@Pace:
@Scott: Much to my wife’s demise, I took the exhaustive search folders and notes with me on vacation. A little history on the exhaustive search program – The first program was tuned to search widths less than 2048. Then it was rewritten to search larger widths, but had a restriction that it could only work with primes less than 256. For the widths of interest, this was not a concern, a simple VB program tested the remaining primes whenever a pattern was found. The current version has the ability to break the search into segments (5760 separated branches) so in the event of power loss the search was not lost. Also, the program has four search parameters, which may be useful to this project.
The parameters are search for:
1) pi(w)+1 elements
2) k(w) elements
3) kb(w)+1 elements
4) kb(w) elements
Type 4 searches are my main objective, as the number of unique patterns is of major interest for current study, but the type 2 searches could be modified to k(w)+1 and may prove beneficial for this project. Quick note is k(w) is first occurrence, while kb(w) has an additional restriction that both the first and last element of the tuple must be a prime, this allows pre-pruning the search tree, one residue class can be removed because of the first element, and an additional element can be removed when the width is a multiple of the search prime plus one. Right now I am looking into making the program able to be distributed, where a width and a block of the 5760 branches can be run on a computer and returns the results.
@xfxie: WOW, love the work you are doing. I have been following your progress, and occasionally testing the intermediate widths for kb(w) values (the gray erratic line in http://www.opertech.com/primes/trophy.bmp ) Impressive! The best fit line is not implying linearity, but is a metric to measure improvement. When searching stopped, the rate was an additional packed prime for every increase of 267 in width. The work you have done in the past week has this now at 265 !!! (If you keep this up the k-tuples conjecture may be in jeopardy) I have not integrated your work into the current patterns database yet, due to the nature of embedded patterns, I plan to purchase a separate hard drive and add a single pattern at a time so a single core residue set does not dominate. Also, here real soon I hope to do a quick internal gap study, as I believe your search routines use a ‘Greedy’ algorithm, which tends to produce two large gaps instead of many small gaps. If you are using existing tuple core residue sets, this may not be true (hopefully you are).
@Drew: Having some deja-vu here. You are running into one of the reasons I insisted to find and retain ALL patterns for a specific kb(w) search. To save some serious time, original searching needed an good approximate start value for k, to do this tuples were partitioned similar to your ‘lower bound’. Values calculated by adding two tuples eg. kb(2269)=335 and kb(2655)=385 implying kb(4925)<=370 could be improved by using existing patterns one at a time to extend the width and verifying that no section in the new tuple violated a maximum density condition determined by the known smaller tuple data. I wrote a spaghetti code program to do this, and probably could duplicate it to achieve a better lower bound for a specific k0.
@Drew: There was mention of embedded tuples in a previous post. Many 'best' tuples are extensions of an existing smaller tuple, and an attempt to use this was tried. But of more interest was the largest embedded tuple that was smaller than half the target tuple width. Also, a study was done on multiple smaller tuple patterns that were embedded, in an attempt to find start search criteria.
Not sure who this is for, as I cannot find the post now, but the Merten's theorem is of major relevance and excited to see work heading in that direction.
I'm sure I've missed some postings, I will get caught up soon.
@Drew: Here are some rough timings for exhaustive search of kb(w), your search for k(w)+1 would be faster, as there would be at least one less branch to search, allowing an even earlier exit condition.
10/8/2008 >> w=2203 completed
1/7/2009 >> w=2263 completed (30 widths)
2/1/2009 >> w=2303 completed (20 widths)
2/7/2009 >> w=2311 completed (4 widths)
9/12/2009 >> w=2331 completed (10 widths)
Problem with the above is there were many idle times in the above, but this could give you a rough benchmark for time consumed. Also, as you have already seen (aka k=198 in above post) every width has it’s own time fingerprint.
As for using SIMD and tight assembly code. the inner loop in the program consumed somewhere around 68 clock cycles. (It purred nicely).
@Andrew: Ran a test for you, here is an output log for doing a type 2 test – search for k(w)+1. Using the program as is requires checking each width because of the restriction that both first and last elements are prime locations. The program could be altered to remove that restriction, thereby allowing checking only w: 1257 to verify that k:198 cannot happen earlier. This would cost 20% more time max. Would be major reduction in time. For some reason I cannot get the compiler on the laptop to recognize the SIMD Boolean instructions or I’d start altering it today.
Using program as is : approx 48 minutes to verify all widths
Altering program : approx 5 minutes to verify next smallest width
When in the larger widths this could be major.
——-
06 14:16:46 2) w: 1237 k: 197 (0)
06 14:17:58 2) w: 1237 k: 197 failed (1-5760)
06 14:19:19 2) w: 1239 k: 198 failed (1-5760)
06 14:21:05 2) w: 1241 k: 198 failed (1-5760)
06 14:23:05 2) w: 1243 k: 198 failed (1-5760)
06 14:25:22 2) w: 1245 k: 198 failed (1-5760)
06 14:28:38 2) w: 1247 k: 198 failed (1-5760)
06 14:32:09 2) w: 1249 k: 198 failed (1-5760)
06 14:38:08 2) w: 1251 k: 198 failed (1-5760)
06 14:42:49 2) w: 1253 k: 198 failed (1-5760)
06 14:50:08 2) w: 1255 k: 198 failed (1-5760)
06 14:58:20 2) w: 1257 k: 198 failed (1-5760)
06 15:02:38 2) w: 1259 k: 199 failed (1-5760)
——–
@Thomas: Thanks for the timings. It would be interesting to know how they scale with k/w (i.e. how does the shape of the curve compare to the chart in #11, say as k goes from 2 to 200 with w=H(k)+1).
Overnight, the exhaustive search program was set to iterate through a list of w’s and search a single sub-branch of the tree. The w’s are two smaller than the smallest known value for each k.
(eg. a pattern of 342 exists for a width of 2329) Verifying that no pattern of 342 exists in a width of 2327 would thereby set 2328 as the optimal diameter for k0=342.
Complete timings are erratic, but show some of the overall growth. If time permits I may redo the test using a different branch, this test was branch 642 or 5760. The pattern tested probably had an early exit for width 2409, other patterns will probably have timings closer to those of 2405.
Width K0 1 branch Complete
w:2327 k:342 9m:33s 38.2 days
w:2339 k:343 30m:52s 123.5 days
w:2341 k:344 38m:47s 155.1 days
w:2353 k:345 33m:49s 135.3 days
w:2357 k:346 34m:13s 136.9 days
w:2363 k:347 15m:44s 62.9 days
w:2375 k:348 48m:42s 194.8 days
w:2381 k:349 19m:55s 79.7 days
w:2387 k:350 23m:01s 92.1 days
w:2393 k:351 1h:18m:59s 315.9 days
w:2399 k:352 15m:27s 61.8 days
w:2405 k:353 36m:33s 146.2 days
w:2409 k:354 9m:01s 36.1 days
w:2417 k:355 14m:56s 59.7 days
w:2439 k:356 2h:23m:02s 572.1 days
w:2443 k:357 1h:46m:02s 424.1 days
w:2451 k:358 3h:16m:02s 784.1 days
w:2459 k:359 1h:03m:13s 252.9 days
w:2473 k:360 49m:09s 196.6 days
w:2479 k:361 1h:26m:24s 345.6 days
w:2483 k:362 1h:46m:50s 427.3 days
w:2489 k:363 1h:14m:59s 299.9 days
w:2495 k:364 19m:17s 77.1 days
w:2501 k:365 1h:23m:28s 333.9 days
w:2515 k:366 2h:25m:19s 581.3 days
w:2519 k:367 1h:03m:32s 254.1 days
w:2521 k:368 1h:08m:01s 272.1 days
@Thomas: great to know the calculation is useful. I am currently migrating the software and its database to an idle machine. Seems the process is not fast due to there are millions of small k-tuple files in the “database”. But hopefully, it might continue to generate new results after the migration.
Have a couple more conditional jump statements to optimize and the exhaustive search program is ready to target k0 values.
Is there a specific k0 that we want targeted ??
The program can currently handle widths up to 3400, by changing a constant this value can be increased. It tests primes up to 255, secondary testing can prove admissibility for remainder of the primes.
(Note: for the 5414 width, the largest destructive prime is 239)
The current target remains k0=720 (width 5414), but it is possible that this could come down to something close to k0=630 (width 4660). I suggest holding off on any major computations until this is nailed down, but if it is easy to get timings for 1 branch just to see what things look like, that would be interesting.
Reblogged this on Observer.
I’m afraid I haven’t been following this closely, and only started reading through the relevant posts this evening, so please excuse me is what I am about to say is appallingly misinformed. Apologies in advance for the lack of latex. I don’t quite know how to do it in wordpress comments.
It seems to me that the residues you sieve with don’t matter in the grand scheme of things, and only the location you look for the survivors counts. The reason I say this is that given some set of pairs of residues and primes, (r_i,p_i), we could always compute some number C by solving C = -r_i mod p_i using the Chinese Remainder Theorem, and then adding this constant to the elements of H to form a new admissible set of the same cardinality, where now all of the residues are non-zero.
So, this seems to suggest that we may as well focus on sieving out the zero residues, and instead simply choose where to look strategically. But this should be fairly simple: for any given interval of T integers, each prime p_i eliminates either ceil(T/p_i) or floor(T/p_i) integers. Clearly we would like as few integers to be eliminated as possible, meaning we want to make sure that different primes eliminate the same integer as often as possible. But there is no reason to believe that we should find this around 0, but rather around the product of all the primes less than or equal to k_0. Let X = \prod_(i:p_i<=k0) p_i. Then if we look at intervals centred on X, it should minimize the number of integers eliminated, by maximizing the number of times any tuple of primes less than or equal to k_0 eliminate the same integer, and hence minimize the total interval required to find an admissible set. The size of the interval required should then be straight-forward to calculate directly from k0.
On closer inspection, it seems this is effectively the same as the Hensley-Richards approach, so please feel free to ignore/delete my comments.
Also, I should have suggested intervals starting at X-1 to maximize the number of times tuples occur (centering minimizes them), though this has the disadvantage of ensuring that ceil(T/p_i) integers are eliminated, so it was incorrect for me to claim it necessarily minimized the interval, although it does appear to be within |{p_i}_i| of the actual minimum.
@xfxie: I notice that the submission server was down for several hours today due to a communications problem with the back end. It’s back up now and your recent submissions have been processed.
@Joe: You are entirely correct that choosing the interval to sieve and choosing the residue classes to sieve are mathematically equivalent. Without loss of generality we could assume we always sieve the interval [0,d] (where d is the diameter), in which case the only choice is the set of residue classes S to sieve, or we could alternatively assume that we always sieve an interval [s,s+d] using the zero residue classes, in which case the only choice is choosing the location s (the approximate value of d is easy to determine, both asymptotically and in practice). But as I noted in the blog post, the integer s corresponding to a particular set of residue classes S (via the CRT) will, in general, be extremely large, making it impractical to test even a miniscule fraction of the possible values of s.
Remarkably, using a small value of s (on the order of k0) combined with a particular method of constructing S (start with a Schinzel sieve and extend it greedily), works surprisingly well — this is the basis of the so-called “greedy-greedy” algorithm, it chooses s and S together, rather than fixing one or the other. As Terry noted in https://sbseminar.wordpress.com/2013/06/05/more-narrow-admissible-sets/#comment-24283, there is some theoretical justification for why this works, and it may be possible to prove that it gives a small asymptotic advantage over other methods that have been analyzed, at least on a heuristic basis (see Section 1 of the progress report at http://terrytao.wordpress.com/2013/06/30/bounded-gaps-between-primes-polymath8-a-progress-report/).
A minor remark about Avishay’s note: one can refine Claim 1.3 slightly by making some considerations modulo 6. Because is constant in fairly large regions, the gain one gets from this is disappointingly limited, though. For our main case of interest
is constant in fairly large regions, the gain one gets from this is disappointingly limited, though. For our main case of interest  , it doesn’t even help at all (but maybe it could if Engelsma’s tables become extended). Here the lower bound reads
, it doesn’t even help at all (but maybe it could if Engelsma’s tables become extended). Here the lower bound reads 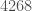 (which improves to
(which improves to 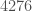 if one uses Drew’s trick from #7). For
if one uses Drew’s trick from #7). For  Avishay’s bound of
Avishay’s bound of  improves to
improves to  (or from
(or from  to
to  using Drew’s trick).
using Drew’s trick).
In any case, here’s an example of such a finer analysis:
Let![S \subset [0,d_1 + d_2 - 1]](https://s0.wp.com/latex.php?latex=S+%5Csubset+%5B0%2Cd_1+%2B+d_2+-+1%5D&bg=ffffff&fg=444444&s=0&c=20201002) be an admissible set of size
be an admissible set of size  . We may assume that $0 \in S$. Let
. We may assume that $0 \in S$. Let ![S_1 = S \cap [0,d_1-1]](https://s0.wp.com/latex.php?latex=S_1+%3D+S+%5Ccap+%5B0%2Cd_1-1%5D&bg=ffffff&fg=444444&s=0&c=20201002) and
and ![S_2 = S \cap [d_1 + d_2 - 1]](https://s0.wp.com/latex.php?latex=S_2+%3D+S+%5Ccap+%5Bd_1+%2B+d_2+-+1%5D&bg=ffffff&fg=444444&s=0&c=20201002) . Clearly
. Clearly 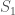 and
and 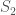 are admissible, so
are admissible, so  and
and  , from which Avishay’s claim follows.
, from which Avishay’s claim follows.
Now suppose that . Since
. Since 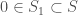 , this implies that
, this implies that  and
and  . This gives the following candidate boundary points of
. This gives the following candidate boundary points of 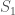 and
and 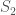 , respectively:
, respectively:

 . But in many cases mod 3 one can do better. For instance, assume that moreover
. But in many cases mod 3 one can do better. For instance, assume that moreover  . Then
. Then

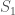 is contained in the smaller interval
is contained in the smaller interval  or
or 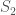 is contained in the smaller interval
is contained in the smaller interval  , from which
, from which
 .
.
This already implies that
By admissibility this means that either
If one makes a similar analysis for all cases , one obtains the following (I just copy-paste the Magma function I used; an output [[a,b],[c,d]] should be read as
, one obtains the following (I just copy-paste the Magma function I used; an output [[a,b],[c,d]] should be read as  , while an output [[a,b]] should be read as
, while an output [[a,b]] should be read as  ; here
; here 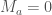 as soon as
as soon as 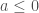 ).
).
function boundingpair(d1,d2)
// WE ASSUME d1 + d2 NOT TOO SMALL
case [d1 mod 2, d2 mod 2]:
when [0,0]:
case [d1 mod 3, d2 mod 3]:
when [0,1]: return [[d1-3,d2-1],[d1-1,d2-3]];
when [1,1]: return [[d1-3,d2-1],[d1-1,d2-3]];
when [1,2]: return [[d1-3,d2-1],[d1-1,d2-5]];
when [1,0]: return [[d1-1,d2-3]];
when [2,1]: return [[d1-1,d2-3]];
else return [[d1-1,d2-1]];
end case;
when [0,1]:
case [d1 mod 3, d2 mod 3]:
when [0,0]: return [[d1-3,d2],[d1-1,d2-2]];
when [1,0]: return [[d1-3,d2],[d1-1,d2-2]];
when [1,1]: return [[d1-3,d2],[d1-1,d2-4]];
when [1,2]: return [[d1-1,d2-2]];
when [2,0]: return [[d1-1,d2-2]];
else return [[d1-1,d2]];
end case;
when [1,0]:
case [d1 mod 3, d2 mod 3]:
when [0,1]: return [[d1-2,d2-1],[d1,d2-3]];
when [2,1]: return [[d1-2,d2-1],[d1,d2-3]];
when [0,2]: return [[d1-2,d2-1],[d1,d2-5]];
when [0,0]: return [[d1,d2-3]];
when [1,1]: return [[d1,d2-3]];
else return [[d1,d2-1]];
end case;
when [1,1]:
case [d1 mod 3, d2 mod 3]:
when [0,2]: return [[d1-2,d2-2],[d1,d2-4]];
when [2,2]: return [[d1-2,d2-2],[d1,d2-4]];
when [0,0]: return [[d1-2,d2-2],[d1,d2-6]];
when [0,1]: return [[d1,d2-4]];
when [1,2]: return [[d1,d2-4]];
else return [[d1,d2-2]];
end case;
end case;
end function;
typos:

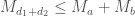 …
…
* the formula that did not parse should be
* … while an output [[a,b]] should be read as
Maybe one more lower bound: for this gives
this gives  (but this should be close to the point where inclusion-exclusion takes over).
(but this should be close to the point where inclusion-exclusion takes over).
@Wouter: thanks for this. My guess it that for 1783 one can do better than 12240 using inclusion-exclusion, but I haven’t tried this yet. I’ll do this when I get a chance (but if someone else wants to run this computation, please do!).
Hi Drew, if you want I can gather data for the lower bound part of the paper. I’ve now also implemented Avishay’s inclusion-exclusion method in Magma. It works reasonably fast, but an implementation in C / assembly would of course allow one to push things further. As I don’t master these languages I’d have to leave that to someone else. But maybe it’s not too important to push the very limits here?
In any case, you’re right that exclusion-inclusion will improve the bound for 1783. When combined with an exhaustive search up to or (if we are patient)
or (if we are patient)  , it looks like one will end up with a lower bound of about 12700 (vs. 12240).
, it looks like one will end up with a lower bound of about 12700 (vs. 12240).
@Wouter: That would be great! I am playing around with a C implementation that combines inclusion-exclusion with a pruned search (as in #11), but I don’t know yet how well it will work. In any case it would be good to have a baseline to compare against. I would also be curious to know the running times for various choices of parameters.
In addition to generating lower bound data for the paper, it would also be nice to fill in the blank spots in tables on the Wiki, even in cases where inclusion-exclusion doesn’t give as good a bound as partitioning (just for the sake of comparison).
http://michaelnielsen.org/polymath1/index.php?title=Finding_narrow_admissible_tuples#Benchmarks
Hi Wouter. I did manage to get my inclusion/exclusion C code working, but its still not as fast as it should be — I need to play with it some more, but I want to make sure it is correct first.
I get the same answers you posted for 342 (2046 at 13, 2072 at 17, and I get 2096 at 19), and for 632 (3976 at 13 and I get 4020 at 17).
But for k=2000 I get a better lower bound than Avishay’s 14082 at 17, I get 14176 (using inc/exc primes up to 173). And at 13 I get 14046 (using inc/exc primes up to 167). I would be curious to know what you get for k=2000 using p_exh=13 and 17.
And for 1783 I get 12408 at 13 (largest inc/exc prime 157) and 12520 at 17 (largest inc/exc prime 167).
There are two optimizations that I am using (besides pruning and early abort), that are worth mentioning in case you aren’t already using them in your Magma code. (1) wlog I assume 0 is always in the admissible tuple, so I never consider residue classes 0 mod p. (2) As soon as the inc/exc depth 2 bound for a given p drops goes negative I don’t bother trying any larger p’s. In theory this might give me a worse bound, but so far I haven’t seen this.
Hi Drew, I aborted my computations because I wanted to make a couple of adjustments. But for p_exh = 13, k = 2000 I would have ended up between 14000 and 14048, and for p_exh = 13, k = 1783 I would have found a value between 12400 and 12410. So your outcomes look compatible.
I used the same optimizations as you did (and I also aborted as soon as the contribution of LB_p dropped to negative), but I should rethink the way I nest the loops. One other thing that frustrates me is that I don’t find a satisfactory way of exploiting the symmetry x -> -x. Did you?
I indeed temporarily copy-pasted Avishay’s bounds to the p_exh = 17 row, but it was to be expected that they are not optimal (Avishay computed upper bounds for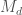 for a couple of smaller values of d, and then used partitioning to bridge the gap).
for a couple of smaller values of d, and then used partitioning to bridge the gap).
In fact, one adjustment I wanted to make is the following way of zooming to the “right” value of d, given k. But maybe you already do this. We start from a value of d that’s clearly too big to be useful in proving a lower bound on H(k). As before, we iterate over all tuples of residue classes mod 2, 3, …, p_exh (never considering 0 as you said), and for each
of residue classes mod 2, 3, …, p_exh (never considering 0 as you said), and for each  we compute the corresponding inclusion-exclusion bound
we compute the corresponding inclusion-exclusion bound  . If
. If 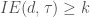 , we gradually drop d by 2 and reconsider the same $\tau$ until
, we gradually drop d by 2 and reconsider the same $\tau$ until  . We then proceed with the next tuple. The point is that there is no need to reconsider the previous $\tau$'s.
. We then proceed with the next tuple. The point is that there is no need to reconsider the previous $\tau$'s.
Now I'll call it a night, but tomorrow I'll try to confirm your lower bounds.
I updated the partition bounds in the Wiki for k_0 > 5000 to use the lower bounds at 370 and 385 (but these do not use your mod 6 optimization). A complete list of bounds for k_0 up to 4000000 is available at
http://math.mit.edu/~drew/partition_bounds_342_plus_4000000.txt
We can improve the partition bounds slightly by using H(343) >= 2334. This can proved as follows:
1) Engelsma proved that there are exactly 16 admissible 342-tuples with diameter 2328, and I was able to compute these, see
http://math.mit.edu/~drew/sequences_342_2328.txt. One can check that in all 16 cases adding either the element 2330 or 2332 does not yield an admissible 343-tuple.
2) It follows that any admissible 343-tuple with diameter 2332 would (up to translation) have to look like 0 … 2330 2332, but this is inadmissible mod 3.
@Wouter: can you rerun your mod 6 optimization using H(343) >= 2334 to see if it changes any of the bounds in the Wiki? I note that it already improves the bound for 10719 to 74076.
Hi Drew, there was a subtle bug in my code: my lower bound was sometimes smaller than yours. But now my outcomes match with yours (at least in the p_exh = 13 cases, p_exh = 17 is still running, so I’ll double-check that too). I already filled them out on the wiki.
So now I can gradually start filling the grid. It would be good to check a few more cases against each other.
I agree with your bounds for k=672 and k=1000 with p_exh = 13. With p_exh = 17 I get 4310 and 6660 respectively.
Ok, I filled them in. The new bound on H(343) doesn’t help for the first few k’s in the table (up to k = 1000). I’m currently running a bigger computation.
As a generalization of Wouter’s mod 6 suggestion in #25, one can use the following. Let be the maximum
be the maximum 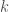 for which there exists an admissible
for which there exists an admissible 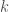 -tuple of diameter
-tuple of diameter 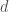 . Let
. Let  denote the set of all tuples
denote the set of all tuples  obtained by sieving the interval
obtained by sieving the interval ![[0,d]](https://s0.wp.com/latex.php?latex=%5B0%2Cd%5D&bg=ffffff&fg=444444&s=0&c=20201002) of one residue class modulo each prime
of one residue class modulo each prime  (note that
(note that 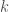 may vary within
may vary within  . Then for any bound
. Then for any bound 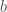 we have
we have
So far I haven't been able to make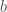 large enough to improve the bounds for H(632), but using
large enough to improve the bounds for H(632), but using 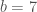 this does improve the lower bound for H(1000) to 6810, for example.
this does improve the lower bound for H(1000) to 6810, for example.
Just a quick follow-up on Wouter’s suggestion in #32 — I implemented this and it significantly speeds up the process of obtaining lower bounds via inclusion/exclusion. This is what I am currently using to fill in the expanded Benchmarks table on the wiki at
http://michaelnielsen.org/polymath1/index.php?title=Finding_narrow_admissible_tuples#Benchmarks
@Wouter: for k0=6329 and p_exh=17 I get the inclusion-exclusion bound 49,356. This is the only case where I haven’t seen an improvement over the bounds Avishay originally posted (his bound for 6329 is posted at
https://sbseminar.wordpress.com/2013/06/05/more-narrow-admissible-sets/#comment-24008). I’m wondering if maybe there is a typo in this post. Have you been able to reproduce this bound?
Hi, my slowish implementation is still running on this entry, and it might take a few more days to decide. But currently it already tells me that the lower bound will be at most 49,356. So, me too, I find an inconsistency with Avishay’s post. I would also guess/hope that there’s a typo?
I think it probably makes sense to go with the more conservative value 49,356 that we appear to agree on (but let me know if your bound changes). If avishay wants to correct us on this he is certainly welcome to.
Regarding #38, I realized my implementation was incorrectly assuming h_k=d after sieving [0,d], but this need not be the case, h_k will be smaller than d in cases where d gets sieved. I’ve updated the wiki to reflect the slight improvements one gets by correcting this mistake (so far just for k0 up to 34429, I’ll update the others as the computations finish).
Just to follow up on #41 and #42, it looks like we both eventually arrived at the same lower bound 49,344 for k=6329 using p_exh=17, so I have updated the wiki accordingly.