Gromov-Witten Invariants and Topological Field Theory

A few days ago, John Mangual requested that one of us secret blogging seminarians write a post explaining what Gromov-Witten invariants are all about.  I volunteered to do this, which puts me in an awkward position.  Gromov-Witten theory is a big subject, and there are a lot of good introductions to the subject (e.g., Behrend’s Algebraic Gromov-Witten Invariants). It’s not clear that I can do much in a single blog post.

So I’m going to limit the scope of this post somewhat.  I’d like to explain in what sense Gromov-Witten theory is a topological field theory.   Caution: This may involve some rambling.    If you’re curious, come below the fold.

Let’s start with the following observation.  If X is a smooth projective complex variety, then the cohomology algebra H^*(X,\mathbb{Q}) is a supercommutative Frobenius algebra. The inner product comes from integration.

(v,w) = \langle [X], v \cup w \rangle

Poincare duality implies that the inner product is non-degenerate.  So we have a finite-dimensional Frobenius algebra on our hands. One of Folk’s theorems tells us that commutative Frobenius algebras are the same thing as two-dimensional TQFTs, so it’s natural to wonder if we can build up some sort of 2d topological field theory by assigning H^*(X,\mathbb{Q}) to the circle, and multiplication to the pair of pants.  (If the supercommutativity bothers you, just take the even subalgebra.)

I want to reformulate this statement in a way that suggests further structure.

Consider the moduli stack \overline{M}_{g,I}, which classifies stable genus g curves having marked points indexed by a set I.   (A marked curve (\Sigma,\sigma_i) is stable if its automorphism group is finite.)  This is a pretty nice stack.  It’s smooth, its dimension is what you’d expect from deformation theory,  it’s Deligne-Mumford, and it’s compact.   And it’s got a really interesting natural stratification.

The different strata in \overline{M}_{g,I} classify curves having fixed topological types.   The open top-dimensional stratum classifies smooth curves, and the strata of higher codimension classify curves with varying numbers of nodal singularities.   If you want to be precise about this, you use modular graphs to classify the topological types.   The modular graph of a curve consists of

  • a set of vertices, one for every irreducible component of the curve
  • a set of edges, one for every node in the curve.   Edges connect vertices if the corresponding components meet at a node
  • a set of tails, one for each marked point on the curve
  • an integer label g_v on each vertex v, the genus of the associated component.
A Curve & Its Modular Graph

What makes this stratification so remarkable is that each boundary stratum in \overline{M}_{g,I} is a (finite quotient of a) product of simpler moduli stacks, which classify smooth curves.   For example, the substack M_{\Gamma} \subset \overline{M}_{5,3} of curves which have the topological type \Gamma depicted in the example above is ({M}_{2,4} \times {M}_{1,5})/Aut(\Gamma).     The first factor parametrizes complex structures and the positions of marked points and nodes on the left component; the second does the same thing on the right.    And essentially the same thing is true if we take closures.  Continuing with the example, there is a natural surjection

\overline{M}_{2,4} \times \overline{M}_{1,5} \to \overline{M}_\Gamma.

More formally, the collection \{\overline{M}_{g,I}\} of all moduli stacks of stable marked curves is a modular operad.   For any collection of graphs \{\Gamma_j\} and any way of pairing tails in these graphs to make a new graph \Gamma, we get a morphism

\overline{M}_{\Gamma_1} \times \overline{M}_{\Gamma_2} \times ... \times \overline{M}_{\Gamma_N} \to \overline{M}_\Gamma

This operad structure induces an operad structure on the collection of homology groups \{H_*(\overline{M}_{g,I})\}, with a product

H_*(\overline{M}_{\Gamma_1}) \otimes H_*(\overline{M}_{\Gamma_2}) \otimes ... \otimes H_*(\overline{M}_{\Gamma_N}) \to H_*(\overline{M}_\Gamma)

for every way of making a graph \Gamma out of the \Gamma_j.

If you have an operad, the first thing you should do is ask what it would mean for a vector space V to be an algebra over your operad.  I’ll assume that V, like H^*(X),  comes equipped with an isomorphism to its dual.  In this case, saying that V is an algebra over the homology operad of the moduli stack of curves means that we get an operation

T_{[\Sigma/B]} \in Hom(V^{\otimes I}, \mathbb{C}) \simeq Hom(V^{\otimes I \setminus I'},V^{\otimes I'})

for every homology class {[\Sigma /B]} \in H_{dim(B)}({\overline{M}_{g,I}}), and that we can compose these morphisms in ways that correspond to gluing curves together.  You should imagine that we have a copy of V living at each marked point on our curves, and that when we glue curves at marked points, we compose through these copies of V, after using the duality on V to relabel some points as outgoing.

What does this mean when every homology class has degree zero?  Degree zero homology classes are represented by points in \overline{M}_{g,I}, i.e. by curves with marked points.  Since \overline{M}_{g,I} is connected, we can always assume that the curve representing {[ \Sigma]} is smooth.  Explicitly, we can resolve the singularity xy = 0 to xy = t; this is obviously a homotopy, and you should think of it as the opposite of contracting a cycle to a point.

The operation on homology classes sends a collection {[\Sigma_j]} \in H_0({\overline{M}_{\Gamma_j}}) to the homology class in H_0({\overline{M}_{\Gamma}}) represented by the curve you get by gluing the \Sigma_j together at marked points.   Of course, we can always replace this curve with a homologous smooth curve.   So, up to homotopy, the multiplication on degree zero homology classes reproduces the obvious composition on curves with boundary circles.   Which means that an algebra V over the degree zero homology operad \{ H_0(\overline{M}_{g,I})\} is essentially the same thing as a Frobenius algebra.

In particular, H^*(X) is an algebra over the degree zero homology operad.   Hopefully, now everyone still reading is primed to wonder, can we make H^*(X) into an algebra over the full homology operad?

The answer, of course, is yes.  (Wouldn’t you be annoyed if I’d taken you all this way to say “no”?)  This is what Gromov-Witten theory is all about.

To get this operadic structure, we use Kontsevich’s stack \overline{M}_{g,I,d}(X) of stable maps from marked curves to X.   This stack classifies stable triplets (\Sigma,\sigma_i,\phi) consisting of a nodal (not necessarily stable) marked curve (\Sigma,\sigma_i) and a map \phi: \Sigma \to X.   A triplet is stable if it has no automorphisms, i.e. if every unstable component in \Sigma carries a non-trivial maps.   The label d is a homology class in H_2(X); a map \phi has degree d if \phi_*[\Sigma] = d.

Kontsevich’s stack has two really interesting morphisms.  There are evaluation maps ev_i: \overline{M}_{g,I,d}(X) \to X, gotten by evaluating \phi at the marked point \sigma_i.   And there is a morphism

F:{\overline{M}_{g,I,d}(X)}\to {\overline{M}_{g,I}}

which forgets the map to X and contracts any unstable components in(\Sigma,\sigma_i).   So, if we have a collection \{\alpha_i\} of cohomology classes in H^*(X), we can pull them back via the evaluation maps, wedge/cup them together, and then (virtually) push them forwards along the integration map.   This gets us a cohomology class F_*^{vir}({\cup_i ev_i^*\alpha_i}) \in H^*(\overline{M}_{g,I}).   Using Poincare duality on \overline{M}_{g,I}, we can reassemble these data into a morphism

H_*({\overline{M}_{g,I}}) \to Hom(H^*(X),\mathbb{C})

which gives us an operation for every homology class on the stack of curves.  And the geometry of \overline{M}_{g,I,d}(X) will guarantee that we can compose these morphisms, making H^*(X) into an algebra over the homology operad.  The key point is that you can specify a map on a curve with multiple components by saying what the map is on each component; then you can glue these maps together if they match at the nodes.

Rather than going into detail about exactly how H^*(X) becomes an algebra over the homology operad, I want to comment on two interesting features of the construction.

First, for some reason, I said “virtual” pushforward.  That”virtual” guy looks a bit shady, lurking there in the parentheses.  What’s his deal?    And second, it’s probably worth pointing out explicitly:   Gromov-Witten theory isn’t really a topological field theory.   The operations coming from the degree zero homology are topological, but the higher operations do actually depend on a conformal structure, albeit very weakly.    One way of understanding these phenomena is to look at the physical theories which inspired the development of Gromov-Witten theory.

This means that we should study the A-twisted nonlinear sigma model.   I don’t want to get into gory details here,  so let me just review the key points.

  • The spacetime of the sigma model is a Riemann surface with boundary circles, which we’ll denote by \Sigma to make you think it’s an algebraic curve.    The Riemann surface carries a metric \eta.
  • The space of fields in the twisted sigma model is the parity-reversed tangent bundle of the vector bundle on the space of smooth maps whose fiber at a given map \phi \in C^{\infty}(\Sigma,X) is the space of odd 1-forms \chi on \Sigma valued in the pullback \phi^*\Pi T_X of the parity reversed tangent sheaf of X.
  • Functional integration over this space looks a lot like integrating differential forms, because we use Berezin integration for the odd fields.
  • This space of fields carries a natural odd vector field Q, which is basically the de Rham differential reinterpreted; this vector field generates a supersymmetry.
  • The local observables at a point \sigma \in \Sigma (i.e., those which depend only on the jets of the fields at \sigma) which are annihilated by the vector field Q are in correspondence, via evaluation maps at the point \sigma, with closed forms on the target space $X$.
  • Most importantly, functional integration in this theory involves a really amazing localization phenomenon.   Roughly speaking, the path integral measure e^{iS_\eta(\phi,\chi, H,\rho)} d\phi d\chi d H d\rho only gets contributions from an infinitesimal neighborhood of the subspace Hol_\eta(\Sigma,X) of holomorphic maps to X.   (Holomorphic with respect to the complex structure determined by the metric \eta.)  Everything else cancels out.

What this means is that the functional integral reduces to an integral on some nilpotent neighborhood of the space of holomorphic maps.   In particular, the integral of Q-closed local operators can be computed by integrating cohomology classes on the space of holomorphic maps.  (One can show, at a physical level of rigor, that Q-exact classes give vanishing functional integrals, so we can descend to Q-cohomology, which reduces to ordinary deRham cohomology once we restrict to the space of holomorphic maps.)

\int {\Pi_i {\mathcal{O}_i(\phi,\chi)}}e^{i S_{\eta}(\phi,\chi,H,\rho)} d\phi d\chi dH d\rho = \int_{[Hol_{\eta}(\Sigma,X)]} \omega_N \wedge (\wedge_i ev_i^*\alpha_i)

There’s a correction factor here, accounting for the contributions from the normal bundle to the locus of holomorphic maps.  This is the source of the “virtual” integration; when we integrate over the space of holomorphic sections, we naturally pair with the “corrected” fundamental class {[Hol_\eta(\Sigma,X)]^{vir}} = {[Hol_\eta(\Sigma,X)]} \cap \omega_N.

Mathematically, what this means is that, if we want to construct the virtual fundamental class for the fiber of the map-forgetting morphism F: {\overline{M}_{g,I,d}(X)} \to \overline{M}_{g,I}, then we need to introduce a correction factor.   In symplectic geometry, this is usually done by deforming the \overline{\partial}-operator, so that the locus of holomorphic maps has the expected size.  In algebraic geometry, people do something similar, using Behrend & Fantechi’s intrinsic normal cone, which is a stack that knows what the infinitesimal neighborhood of a scheme Z looks like when we embed Z inside any ambient scheme.

Now what about the metric dependence?   How strong should we expect it to be?   Not very strong, obviously, since the equation above indicates that it only depends on the conformal class of the metric.    But what if we vary the conformal structure?    Well, it turns out that the exponentiated action is Q-exact,  i.e., S_{\eta} = Q V_{\eta}, for some function V_{\eta}.   In particular, infinitesimal shifts in \eta change the integrand by a Q-exact cohomology class; hence don’t produce any changes when we pass to the cohomology of Q.

One way of formally realizing this idea is to say that Gromov-Witten theory is a topological conformal field theory, which is a concept that lies midway between topological field theory and conformal field theory.

Mathematically, a topological field theory is a functor to vector spaces from a category whose objects are integers (counting the number of circles) and whose morhisms are cobordisms between these circles.    A CFT is supposed to be a similar gadget, except that the space of morphisms consists of cobordisms equipped with complex structures.   In topological conformal field theories, one instead considers functors from a category whose objects are integers $# of circles) and whose morphisms are chains on the moduli stack of complex structures on bordisms between these circles.    This functor maps to the category of differential graded vector spaces, and has to send the boundary operator on chains to the differential on the vector spaces.

I’m about done at this point, so I’ll finish with one last thought:  It’s these quantum field theory structures that make Gromov-Witten theory so useful for studying problems in enumerative geometry.    Most of the useful equations in Gromov-Witten theory, such as the WDVV equations or the string and dilaton equations and the rest of the Virasoro hierarchy, arise directly from the fact that Gromov-Witten theory is a QFT.

10 thoughts on “Gromov-Witten Invariants and Topological Field Theory”

  1. A. J. wrote:

    It’s not clear that I can do much in a single blog post.

    The main thing a good blog post does is: not too much! There are already plenty of papers that do everything in detail. So, I think good math exposition pays scrupulous attention to leaving out everything that’s not absolutely necessary for telling a good story. This is very difficult, since the niggly nuances wind up absorbing a lot of our attention when we get involved in a subject. But a reader wanting a quick sense of the big picture will be happiest if we paint a picture in broad but clear brushstrokes – with a slight roll of the eyes now and then to indicate that the picture is being simplified.

  2. Hi John,

    Thanks for the gentle criticism. I hope you found the first half of the article good reading, before we went haring off into QFT.

  3. I wasn’t really trying to criticize your post – just reacting to your apology for not covering enough ground.

    I would be very happy simply to understand modular operads a bit better. I’ve seen Ezra Getzler give two beautiful talks on them, and they seem like a great thing, but I don’t understand them very well.

    The algebraist in me wants a “purely algebraic” description of the homology operad you describe here. It can be a lot of fun when you have both a geometrical/topological description and a purely algebraic description of a gadget like this. You mention a nice example: the symmetric monoidal category of 2d cobordism is the free symmetric monoidal category on a Frobenius monoid.

  4. I am also confused by modular operads. Does B denote a substack of \overline{M}_{g,I}, or does it live in some formal cycle space that can have multiplicity? Should the corresponding operation T_{[\Sigma/B]} have some homological degree?

  5. B is the base of a family of curves \Sigma/B, which determines a morphism B \to \overline{M}_{g,I}, which determines a homology class in \overline{M}_{g,I}. You don’t have to worry about the stack structure too much though; we’ve got a Deligne-Mumford space with a nice coarse moduli space, so you can just define the homology of the stack to be the rational homology of the associated space.

    And yes, the operation T has homological degree.

  6. Whoops, looks like I’m almost a year late to this post! But anyway, some questions:
    1. What does “functional integral” mean here? Is this just some kind of synonym for “path integral”?
    2. What is \omega_N? How am I supposed to think of it? Is it some kind of Thom class or Euler class of the normal bundle?
    3. How do you get from the path integral expression \int blah e^blah dblah to the expression \int omega_N wedge ev^*(alpha)?

  7. Hi Kevin,

    I’m working on a longer post explaining the physics perspective on the virtual fundamental class. The idea — very crudely — is that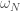 \omega_N (which you’ve correctly identified as the Euler class of the obstruction bundle) can be thought of the Euler class of the normal bundle to the space of holomorphic maps inside the “big” space of fields \{(\phi,\chi,H,\rho)\}. To make this even close to precise, I need to explain how you’re supposed to do the path integral. Which is why you’ll have to wait for a longer post.

  8. AJ- Sounds awesome, I look forward to it!! And thanks for always being so helpful in answering my endless GW-related questions.

  10. in case anyone is still checking the comments here: what does “chains on the moduli stack” mean, in the definition of TCFT? Am I supposed to interpret it as morphisms being the complex of singular chains? (whatever that may mean for a stack)

Comments are closed.