The Weil Conjectures: The approach via the Standard Conjectures

The aim of this post is to outline a strategy for proving the Weil conjectures, proposed by Grothendieck and others. This strategy is incomplete; at various stages, we will need to assume conjectures which are still open today.

Our aim is to prove:

Theorem:
Let X be a smooth projective variety, over a field of any characteristic. Let H^* be a “reasonable” cohomology theory. Let \omega \in H^2(X) be the hyperplane class for a projective embedding of X. Let F be an automorphism of X, such that F^* \omega = q \omega. Then the eigenvalues of F^*: H^r(X) \to H^r(X) are algebraic numbers and, when interpreted as elements of \mathbb{C}, have norm q^{r/2}.

In previous posts, we gave for a proof in characteristic zero and a proof in the case that X is a curve. I also explained why I need to say how I am embedding these eigenvalues into \mathbb{C}. Our proof requires all the ideas of these previous posts, plus some new ones.

Let’s be precise about what tricks we are going to use from previous posts.

  • We will use the class \omega, and the adjoint operator L, to put a Hermitian bilinear form \langle \ , \ \rangle_{\omega} on H^r(X). In characteristic zero, this form had the property that it was i^{p-q} times a definite form on H^{p,q}(X).
  • We will build a ring A, whose elements are linear combinations of subvarieties of X \times X, and for which H^*(X) is a module. There will be a trace map T:A \to \mathbb{Q}. It will thus make sense to say that a quantity defined in terms of the trace map is positive, leading us out of the difficulty of coefficients.

We also mention a change of perspective. In past posts, we fixed r and studied H^r(X). In this post, we will usually want to consider all of H^*(X) at once, and only focus on a particular degree towards the end of our arguments.

That said, let’s get started.

Structures on H^*(X)

Write d for the dimension of X.

We write \langle \ , \ \rangle for the pairing \langle \alpha , \beta \rangle = \int_X \alpha \wedge \beta on H^*(X). Here we adopt the standard convention that \int_X \eta=0 for \eta in any degree below the top degree.

It is an easy exercise that \langle F^* \alpha, F^* \beta \rangle = q^d \langle \alpha, \beta \rangle.

The ring of correspondences A

Let A^{2i} be the sub-\mathbb{Q} vector space of H^{2d-2i}(X \times X) spanned by algebraic cycles of codimension d+i. Note that i ranges from -d to d, and that A^0 is what was called A in a previous post. In this post, we will want to work with a larger ring, so we change notation and set A := \bigoplus_{i=-d}^d A^{2i}.

We put a ring structure on A by C \cdot D = (\pi_{13})_* (\pi_{12}^*(C) \cup \pi_{23}^*(C)), where \pi_{ij} are the three projections from X \times X \times X to X \times X. Note that A is a graded ring and H^*(X) is a graded A module. (This explains our funny indexing.) The diagonal \Delta \subset X \times X is the multiplicative identity.

We define the linear map T:A \to \mathbb{Q} by intersection with the diagonal \Delta. (So T is zero on A^i for i \neq 0.) From several uses of Kunneth’s theorem, we can prove the analogue of the Lefschetz trace formula:

\displaystyle{T(C) = \sum_{i=0}^{2d} (-1)^i Tr(C^* : H^i(X) \to H^i(X))}

Note that the left hand side is in \mathbb{Q}, while the individual terms on the right are only in the coefficient ring of our cohomology theory.

Define an anti-involutation C \to C^T of A by switching the components of X \times X. We have \langle C^T \alpha, \beta \rangle = \langle \alpha, C \beta\rangle.

Write [F] for the graph of F; an element of A^0. We have [F] [F]^T = [F]^T [F]= q^d \Delta. Multiplication by [F] acts on H^*(X) by F^*.

Let H in X be a hypersurface representing \omega. Embed H into X \times X along the diagonal and write [\omega] for the resulting class in A^2. Multiplication by [\omega] acts on H^*(X) by cup product with \omega. Here we see a preview of our strategy: Every important operation on H^*(X) will be shown (or conjectured) to be the action of some element of A.

The condition that F^* \omega = q \omega translates to the condition

[F] \cdot [\omega] = q [\omega] \cdot [F].

Conjecture C

It would be convenient to be able to isolate the action of A^0 on one particular cohomology group H^i(X). In our previous post, we did this with the operators e_0, e_1 and e_2. The construction of the corresponding operators in the current setting is

Grothendieck’s Conjecture C
There are idempotents e_0, e_1, …, e_{2d} in A^0, so that e_i acts by 1 on H^i(X) and by 0 on H^j(X) for j \neq i.

There are precisely one element of H^{2d}(X \times X) which is a candidate for e_i (exercise!), so this conjecture may be restated to say that this element in the image of the algebraic cycles of X \times X. Also, it is not hard to see that these classes in H^{2d}(X \times X) are mutual commuting and orthogonal, so the e_i, should they exist, are likewise. We will later see that conjecture C follows from other needed conjectures.

Assuming conjecture C, we can put a double grading on A: we have

A = \displaystyle{\bigoplus e_i A e_j \quad A^{k} = \bigoplus e_{i+k} A e_i}.

We define A^{i \leftarrow j} := e_i A e_j. (Warning: I just made this notation up.) So A^{i \leftarrow j} A^{j \leftarrow k} \subseteq A^{i \leftarrow k}.

Here is an interesting application of conjecture C: Assuming conjecture C, the following statement is well meaningful and true:

\displaystyle{ T(e_i [F]^k e_i) = (-1)^i \ Tr((F^k)^* : H^i(X) \to H^i(X)) }.

In particular, the right hand side is a rational number. We conclude, given Conjecture C, the eigenvalues of F^* on H^i(X) are algebraic numbers.

I think that conjecture C is not expected to be true if we define A using integer combinations of algebraic cycles; that \mathbb{Q}-combinations should be needed. If anyone can confirm this, that would be nice!

Conjecture B

We want to define the bilinear form \langle \ , \rangle_{\omega} from our previous post. We would like to take the definition to be the following: The inner product \langle \alpha , \beta \rangle_{\omega} on H^r(X) is given by \langle \alpha, Q^d_r([\omega], [\Lambda]) \beta \rangle, where Q^d_r is the noncommutative polynomial from the previous post.

But what is \Lambda?

Grothendieck’s Conjecture B
Multiplication by \omega^{d-r} is an isomorphism between H^{r}(X) and H^{2d-r}(X). There is a class [\Lambda] in A^{-2} which acts by the operator \Lambda introduced in the previous post.

The purpose of the first sentence is to make our previous discussion of \Lambda meaningful.

In fact, the idempotents e_r can be written as polynomials in [\omega] and [\Lambda] (exercise!). So, if we assume conjecture B, we can deduce conjecture C.

We prefer to work with all of H^* at once. So we define

\displaystyle{ Q := \sum_{r=0}^{2d} Q^d_r }

and

\displaystyle{ \langle \alpha, \beta \rangle_{\omega} = \langle \alpha, Q \beta \rangle.}

This is just the direct sum of our constructions on the individual H^r(X)‘s. The element Q lives in \bigoplus A^{(d+r) \ \leftarrow \ (d-r)}.

We have

[F][\omega] = q [\omega] [F] and [F][\Lambda] = q^{-1} [\Lambda][F]         (*).

From these identities, one can deduce
Proposition Assuming Conjecture B, so that the statement is meaningful, we have \langle [F] \alpha, [F] \beta \rangle_{\omega} = q^{2r} \langle \alpha, \beta \rangle_{\omega}, for \alpha and \beta in H^r(X).

Looking for positive definiteness

We have now (assuming conjecture B) been able to define a bilinear form \langle \ , \ \rangle_{\omega} on H^r(X) such that q^{-r/2} F^* is self-adjoint, and which, in characteristic zero is the bilinear form which appeared in our earlier proof. We wish to, roughly speaking, show that this form is positive definite.

Taking a hint from our proof in the curve case, what we will actually do is create an operation \dagger on A which corresponds to taking the adjoint with respect to this form. We will then show that (C,D) := T(C^{\dagger} D), from A \times A to \mathbb{Q}, is positive definite.

Here is the definition: It is not hard to show that Q is a unit in A. For C \in A, define

\displaystyle{ C^{\dagger} := Q^{-1} C^T Q.}

We leave it as an exercise that

\displaystyle{ \langle C \alpha, \beta \rangle_{\omega} = \langle \alpha, C^{\dagger} \beta \rangle_{\omega}}.

Using the relations (*), we have F^{\dagger} F = F F^{\dagger} = q^r \Delta on H^r(X).

We now want to establish:

Key Conjectural Lemma:
The \mathbb{Q}-valued bilinear form (C,D) := T(C^{\dagger} D) on A is (-1)^r times a positive definite-form on A^{r \leftarrow r}.

This sign seems to be missing from Kleiman’s article. Presumably, he has hidden it somewhere I have not noticed. Perhaps the reader should take this as a warning not to trust my signs!

Here is something that bothered me. In characteristic zero, \langle \ , \rangle_{\omega} is not positive definite on H^r(X). Rather, it is i^{p-q} times a positive definite form. So why should Tr(C^{\dagger} D) be positive definite on A^{r \leftarrow r}? The point is that C and D will preserve each summand H^{p,q}(X) of H^r(X), so we can compute adjoints on each summand separately. On each summand, the fact that \langle \ , \rangle_{\omega} is i^{p-q}-definite will imply that Tr(C^{\dagger} D) is (-1)^{p-q} = (-1)^r-definite. The key point here is that, if \dagger is the adjoint with respect to either a positive or a negative definite inner product, then Tr(C^{\dagger} D) is positive definite! In positive characteristic, we don’t have the Hodge decomposition, but its shadow is felt in this form.

If we have the Key Conjectural Lemma, the rest is easy. We write F_r:=e_r F e_r and \Delta_r=e_r \Delta e_r. By Cauchy-Schwartz,

\displaystyle{ (F_r^k, F_r^k) (\Delta_r, \Delta_r) \geq (F_r^k, \Delta_r)^2}

or

\displaystyle{ q^{kr} \dim(H^r(X))^2 \geq Tr(F^k: H^r(X) \to H^r(X) )^2}.

Using this inequality for all $k$, we see that the eigenvalues of F^* on H^r(X) have norm q^{r/2}.

QED

Conjecturally proving the Key Conjectural Lemma

In the curve case, we deduced the conjectural lemma from the Hodge Index Theorem applied to X \times X. We wish to do something similar here.

Since we don’t have a Hodge decomposition anymore, we can’t state the Hodge index theorem as powerfully in characteristic p. However, recall that algebraic cycles always live in degree H^{p,p}. So, by stating a conjecture about algebraic cycles, we can hope to recapture just enough of the Hodge index theorem to do the job. This is:

Grothendieck’s conjecture of Hodge type:
Let Z be a projective algebraic variety of dimension d, and \eta the hyperplane class. Let C^{r}(Z) be the \mathbb{Q}-subspace of H^{2r}(Z) spanned by algebraic cycles. Then multiplication by \eta^{e-r} is an isomorphism from C^{r} \to C^{2e-r}, so we may define C^r_k(Z) in a way analogous how we defined H^r_k(Z) in the previous post. The inner product \int_Z \eta^{e-r} \alpha \beta is (-1)^{k(k-1)/2}-definite on C^r_k(Z).

The Conjecture of Hodge Type, for (Z, \eta) = (X \times X, \omega \otimes 1 + 1 \otimes \omega), implies the Key Conjectural Lemma. I don’t think there is any point in me writing up the details of this. Grothendieck attributes this to “certain arguments of Weil and Serre”, it is also explained in Kleiman’s article.

7 thoughts on “The Weil Conjectures: The approach via the Standard Conjectures”

  1. Great post! I happen to be trying to learn this stuff right now…

    I’ve read explanations of Conjecture D and Conjecture C, and now thanks to you also Conjecture B. What’s Conjecture A?

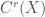  2. Let C^r(X) be the subspace of H^{2r}(X) spanned by algebraic cycles.

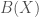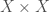    Conjecture A(X) states that \omega^{d-2r} is an isomorphism between C^{r}(X) and C^{d-r}(X). Conjecture B(X) states that the correspondence \Lambda comes from an algebraic cycle on X \times X.

    We have the implications A(X \times X) \to B(X) \to A(X). (See Grothendieck’s Standard Conjectures paper, page 196.) So, as long as we discuss results for all varieties at once, we don’t need to distinguish the two.

  3. Here’s a question which I’ve never really figured out, though I’ve been wanting to know the answer on and off for a while: to what extent do the “standard conjectures” imply (or not) the Riemann Hypothesis in the form of Deligne’s Weil 2 paper? (The main difference between Weil 1 and Weil 2 being that the latter dispenses almost entirely with smoothness/properness assumptions for the main results, and considers cohomology with coefficients in a wide class of sheaves; as a consequence, eigenvalues of Frobenius, though they remain Weil numbers, need not all have the same modulus for a given cohomology space).

    For quite a few important applications in analytic number theory, and for Deligne’s equidistribution theorem, Weil 1 is either insufficient or causes technical difficulties which disappear entirely with the formalism of Weil 2.

  4. This is a great question. I hoped that I would actually have something to say about it but, since I haven’t come up with anything, I want to at least let you know that I read and liked it.

  5. Within the next month or so, I hope to be able to ask this question directly to some people who are likely to know the answer (or at least some answer). If I learn anything interesting, I’ll certainly mention it here or on my own blog.

  6. Pingback: Motive-ating the Weil Conjecture Proof « Secret Blogging Seminar ~
  7. Pingback: Some questions about motives « Secret Blogging Seminar ~

Comments are closed.