The Weil conjectures : Curves

The Weil conjectures : Curves April 19, 2010

Posted by David Speyer in Algebraic Geometry, characteristic p.
trackback

Our goal for today is to prove the following theorem:

Theorem 1: Let $X$ be a projective algebraic curve of genus $g$ and $F$ an endomorphism of degree $q$ . Let $H^*$ be a reasonable cohomology theory. Then the action of $F^*$ on $X$ has eigenvalues which are algebraic integers, with norm $q^{1/2}$ .

For those who know the term, “reasonable cohomology theory” means “Weil cohomology theory”.

The consequence of this theorem, which does not mention cohomology, is

Theorem 2: Let $X$ be a projective algebraic curve of genus $g$ and $F$ an endomorphism of degree $q$ . Then there are algebraic integers $\alpha_1$ , $\alpha_2$ , …, $\alpha_{2g}$ with norm $q^{1/2}$ such that

$\displaystyle{ \# \mathrm{Fix}(F^k) = q^k - \sum \alpha_i^k +1 }$ .

In a previous post, we established this in characteristic zero, by putting a positive definite hermitian structure on $H^1(X, \mathbb{C})$ such that $q^{-1/2} F^*$ became unitary. But, as I discussed last time, we can’t define $H^1(X, \mathbb{C})$ when $X$ has characteristic $p$ . Instead, $H^1(X)$ will be defined over some other field of characteristic zero, like $\mathbb{Q}_{\ell}$ . We will therefore need to know that the eigenvalues of $F$ are algebraic integers before we can even make sense of the statement that they have norm $q^{1/2}$ .

It is possible to take the proof I present here and strip it down to its bare essentials, to give a proof of Theorem 2 which doesn’t even mention cohomology. See Hartshorne Exercise V.1.10. I am going to do the opposite; I will go slowly and focus on what each step is proving about $H^1(X)$ . The essential argument here is Weil’s, although I have modernized the presentation.

The ring $A$

We define a ring $A$ as follows: The elements of the ring are formal sums of curves in $X \times X$ , modulo the relation that $[C] = [C']$ if the curves $C$ and $C'$ have the same class in $H^2(X \times X)$ . We multiply as follows:
$[C] \bullet [C'] = (\pi_{13})_* ( \pi_{12}^* [C] \cdot \pi_{23}^* [C']),$
where the $\pi_{ij}$ are the three projections $X \times X \times X \to X \times X$ .

Fans of This Week’s Finds will recognize this as a slight variant of the category of spans.

Notice that the diagonal, $\Delta$ , of $X \times X$ , is the multiplicative identity of $A$ .

The cohomology groups $H^i(X)$ are modules for $A$ by
$[C] \bullet \alpha = (\pi_1)_* ( [C] \cdot \pi_2^* \alpha)$ . In particular, if $f$ is an endomorphism of $X$ , and $\Gamma$ is the graph of $f$ , then $[\Gamma]$ acts on $H^i(X)$ by $f^*$ .

Let $e_0$ and $e_2$ be the classes in $A$ of $X \times \mathrm{pt}$ and $\mathrm{pt} \times X$ . Then $e_0$ and $e_2$ are orthogonal idempotents. Define $e_1 = \Delta - e_0 - e_2$ , so $e_1$ is also idempotent. Then $e_i$ acts by $1$ on $H^i(X)$ and by $0$ on every other $H^j$ .

Since the $e_i$ are orthogonal idempotents, we have $A = e_0 A e_0 \oplus e_1 A e_1 \oplus e_2 A e_2$ . You can compute that $e_0 A e_0 = \mathbb{Z} e_0$ and $e_2 A e_2 = \mathbb{Z} e_2$ , so all the interest is in $e_1 A e_1$ . We’ll write $A^{1 \leftarrow 1}$ for $e_1 A e_1$ ; so $H^1(X)$ is a $A^{1 \leftarrow 1}$ module.

The involution 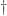$\dagger$

We define an involution $[C] \mapsto [C]^{\dagger}$ of $A$ which sends a curve $C$ to the curve $C^{\dagger}$ obtained by switching the two factors of $X \times X$ . You can check that $\dagger$ sends $A^{1 \leftarrow 1}$ to itself.

In our previous proof, we put a positive definite Hermitian structure on $H^1(X, \mathbb{C})$ .

Exercise: If $X$ is a curve over $\mathbb{C}$ , and $a$ is in $A^{1 \leftarrow 1}$ , then the actions of $a$ and $a^{\dagger}$ on $H^1(X, \mathbb{C})$ are adjoint.

There is a point that confused me when I first learned this stuff. We never mention complex conjugation in the definition of $\dagger$ , so how can we get the Hermitian conjugate? The answer is simple: the maps coming from the action of $A$ are defined over $\mathbb{R}$ (in fact, $\mathbb{Z}$ ). So $a^{\dagger}$ is adjoint to $a$ with respect to both the natural skew-symmetric pairing on $H^1(X)$ , and with respect to its Hermitian complexification. This is just like how, for a real matrix, the transpose and the conjugate transpose are the same thing. The question of whether to think in terms of Hermitian or ordinary bilinear forms is somewhat of an aesthetic choice; perhaps at some later point I will defend my decision to use the Hermitian language.

Let $\Phi$ be the graph of $F$ , and let $\Phi_1 = e_1 \Phi e_1$ . Since $H^1(X)$ is not a complex vector space, we cannot say that $q^{-1/2} \Phi_1$ is unitary.
But there is a statement which still makes sense:

Exercise: We have $\Phi_1^{\dagger} \Phi_1 = q e_1$ .

The linear form $T$

Finally, define a linear form $T: \ A \to \mathbb{Z}$ by $Tr(f) = f \cdot \Delta$ , using the intersection product in $H^*(X \times X)$ . By the Lefschetz trace formula, we have

$\displaystyle{T(f) = Tr(f : H^0(X) \to H^0(X))}$

$\displaystyle{-Tr(f : H^1(X) \to H^1(X))}$

$\displaystyle{+Tr(f : H^2(X) \to H^2(X))}$

Note that the left hand side is an integer, while the right hand side, a priori, need only lie in the coefficient ring of $H^*(X)$ . It is this ability to get an integer, rather than an element of $\mathbb{Q}_{\ell}$ , that will resolve our difficulties with coefficients.

In our previous proof, it was crucial that the Hermitian form on $H^1(X)$ was positive definite. The corresponding result here is

Key Lemma: The $\mathbb{Z}$ -valued inner product $\langle f,\ g \rangle = T(f^{\dagger} g)$ on $A^{1 \leftarrow 1}$ is negative definite.

If $X$ is defined over $\mathbb{C}$ , this follows from the positive definiteness of the Hermitian form. (We pick up the minus sign because $T(f)$ is $- Tr(f : H^1(X) \to H^1(X))$ for $f$ in $A^{1 \leftarrow 1}$ .) But the Key Lemma makes sense over any field because, regardless of what ring our cohomology theory takes coefficients in, the ring $A^{1 \leftarrow 1}$ is still a $\mathbb{Z}$ -module, and the pairing is still $\mathbb{Z}$ -valued.

Proof of the main theorem from the key lemma

$\Phi_1$ acts by zero on $H^0(X)$ and $H^2(X)$ . So $T(\Phi_1^k) = \sum \alpha_i^k$ , where $\alpha_i$ are the eigenvalues of $\Phi_1$ acting on $H^1(X)$ . Since $T(\Phi_1^k)$ is always an integer, we deduce that $\sum \alpha_i^k$ is an integer for every $k \geq 0$ . This immediately implies that the $\alpha_i$ are algebraic numbers and, working a bit harder (exercise!) that they are algebraic integers.

The Key Lemma tells us that $T(f^{\dagger} g)$ is negative definite. So, by Cauchy-Schwartz,

$\displaystyle{ T(\Delta \Phi_1 )^2 \leq T(\Phi_1^{\dagger} \Phi_1) T(\Delta^{\dagger} \Delta)}$ .

In other words,

$\displaystyle{ T(\Phi_1)^2 \leq T(q \Delta) T(\Delta) = (2gq) (2g)}$

and

$\displaystyle{ \sum \alpha_i = T(\Phi_1) \leq 2g \sqrt{q}}$ .

Similar arguments show that $\sum \alpha_i^k = T(\Phi_1^k) \leq 2g q^{k/2}$ for all $k \geq 0$ . From this is follows that $|\alpha_i| \leq \sqrt{q}$ . Applying similar arguments to $q^{-1} \Phi_1^{\dagger} = \Phi_1^{-1}$ , we can also deduce that $|\alpha_i^{-1}| \leq \sqrt{q}$ , so $|\alpha_i|=q^{1/2}$ .

Proof of the key lemma

We consider the form $\langle \ , \ \rangle$ on all of $A$ , instead of just $A^{1 \leftarrow 1}$ . Then $\langle \ , \rangle$ has block form

$\displaystyle{ \begin{pmatrix} 0 & 0 & 1 \\ 0 & * & 0 \\ 1 & 0 & 0 \end{pmatrix}}$

where the middle block is the pairing on $A^{1 \leftarrow 1}$ . So, to prove that $\langle \ , \ \rangle$ is negative definite on $A^{1 \leftarrow 1}$ , it is enough to prove that $\langle \ , \ \rangle$ has signature of the form $(1,r)$ on $A$ . For a proof of this fact, see Hartshorne Theorem V.1.9 and Remark V.1.9.1.

Connection to the Hodge Index Theorem

When our ground field is $\mathbb{C}$ , there is a nice proof that $\langle \ , \ \rangle$ has signature $(1,r)$ on $A$ , using the Hodge index theorem. We’ll be reusing notation from my previous post, so you might want to follow that link to refresh your memory.

By definition, $A \subseteq H^2(X \times X)$ and, in fact, $A$ lies in $H^{1,1}(X \times X))$ . Reusing our notation from an earlier post, $H^{1,1}(X \times X) \cong H^{1,1}_0(X \times X) \oplus H^{1,1}_2(X \times X)$ . But $H^{1,1}_2(X \times X) \cong H^{0,0}_0(X \times X) \cong \mathbb{C}$ , so $H_2^{1,1}(X \times X)$ is one dimensional. Then the Hodge index theorem says that $\langle \ , \ \rangle$ is positive definite on $H^{1,1}_2(X \times X)$ and negative definite on the orthogonal space $H^{1,1}_0(X \times X)$ . We see that $\langle \ , \ \rangle$ has signature $(1,1+2g)$ on $H^{1,1}(X \times X)$ . Its signature on the subspace $A$ must thus be of the form either $(1,r)$ or $(0,r)$ ; it is easy to check that it is the former.

The fact that $\langle \ , \ \rangle$ has signature $(1,r)$ on $A$ can thus be thought of as a shadow of the Hodge index theorem, which remains even when our cohomology theory takes coefficients in an exotic ring. We will return to this point next time, when we tackle Grothendieck’s Standard Conjectures.

About these ads

Comments»

1. The Weil Conjectures: The approach via the Standard Conjectures « Secret Blogging Seminar - May 3, 2010: [...] previous posts, we gave for a proof in characteristic zero and a proof in the case that is a curve. I also explained why I need to say how I am embedding these eigenvalues into . Our proof requires [...]
2. Motive-ating the Weil Conjecture Proof « Secret Blogging Seminar - June 10, 2010: [...] on the attempt to prove the Weil Conjectures through the Standard Conjectures. (Parts 1, 2, 3, 4, 5.) In this post, I want to explain the idea of the category of motives. In the modern formulation [...]

	dymo labelwriters on That trick where you embed the…
	call center outsourc… on That trick where you embed the…
	Www.slatedroid.Com on That trick where you embed the…
	Frure on Including equations in co…
	Frure on Including equations in co…