Characteristic zero analogues of the Weil conjectures: Curves

The quest to prove the Weil conjectures drove algebraic geometry throughout the middle of the twentieth century. It was understood very early that a proof should involve creating a theory of cohomology for varieties in characteristic p. This theory, known as étale cohomology, was developed by Grothendieck and his collaborators. Near the end, there was a period where étale cohomology was established but the hardest of the conjectures, the Riemann hypothesis, was not proved. Several mathematicians* proposed a path which would require proving results that were new even in the complex setting; results now known as the standard conjectures. That route was not taken; instead, Deligne found a different proof with its own insights and innovations.

This is the first of a series of posts sketching how the route through the standard conjectures would have gone. There is of course nothing original here; the usual sources are Kleiman, Grothendieck and Serre. I will try to write in a very classical way; I won’t even leave characteristic zero for the first two posts. And there will be tensor categories before the end!

In today’s post, we will prove the following theorem.

Theorem 1 Let X be a smooth projective curve over \mathbb{C} and F an algebraic endomorphism of degree q > 0. The eigenvalues of F on H^1(X) obey |\alpha|=q^{1/2}.

Counting fixed points

By the Lefschetz trace formula, Theorem 1 has the following consequence:

Theorem 2 There are 2g complex numbers \alpha_1, …, \alpha_{2g} with norm q^{1/2} such that

\#\mathrm{Fix}(F) = q - \sum_{i=1}^{2g} \alpha_i + 1.

More generally,

\#\mathrm{Fix}(F^k) = q^k - \sum_{i=1}^{2g} \alpha_i^k + 1.

When we get around to proving a characteristic p version of this theorem, we will be able to apply this with X a curve over \mathbb{F}_q, and F the Frobenius endomorphism. Then the fixed points of F are the \mathbb{F}_q valued points of X. So Theorem 2 will then be the Riemman hypothesis for curves.

One caveat: We need to count fixed points with multiplicity. For example, the automorphism z \mapsto z+1 of \mathbb{P}^1 has a doubly fixed point at infinity. In the case of the Frobenius, all fixed points are multiplicity one.

The proof

I should acknowledge at the outset that there are easier ways to prove Theorem 1 in the complex case. If the genus of X is 2 or higher, then Riemann-Hurwitz shows that F must be an automorphism, which must have finite order by a result of Hurwitz. So the result simply says that a matrix of finite order has eigenvalues with norm 1. Genus 0 is easy, and we will see soon how to handle the case of genus 1. But I will present a harder proof, which will be closer to the route which works in any characteristic.

Let’s begin with the case where X has genus 1. Theorem 1 is already nontrivial; the homotopy classes of endomorphisms of X are described by 2 \times 2 integer matrices. It is not obvious that the topology \left( \begin{smallmatrix} 3 & 0 \\ 0 & 2 \end{smallmatrix} \right) can’t be realized by a complex map.

Not obvious, but not that hard. X is isomorphic to \mathbb{C}/\Lambda for some lattice \Lambda. Any automorphism F of X lifts to multiplication by z on \mathbb{C} for some z \in \mathbb{C}. The lattice \Lambda is naturally identified with H_1(X, \mathbb{Z}). The action of F on H_1(X, \mathbb{Z}) is multiplication by z, with eigenvalues z and \overline{z}. We have z \overline{z}=q, so |z| = q^{1/2}.

Now, let X be a complex curve of genus g \geq 2. We first try to replicate the above argument; although we will have to modify it in the end.

The cohomology H^1(X, \mathbb{C}) breaks up as a direct sum H^{1,0}(X) \oplus H^{0,1}(X), where H^{p,q} are the cohomology classes which can be represented (in deRham cohomology) by closed (p,q) forms. There are no coefficients on the right hand side because H^{p,q}(X) only makes sense with complex coefficients. Composing

H^1(X, \mathbb{Z}) \hookrightarrow H^1(X, \mathbb{C}) \to H^{1,0}(X),

we get a rank 2g lattice in a g-dimensional complex vector space, and F acts on everything.

Unfortunately, this isn’t enough. We get that F^* is an element of \mathrm{Mat}_g(\mathbb{C}) which preserves a lattice, but that doesn’t restrict its eigenvalues very strongly. There exist examples** of curves X for which there are symmetries of the pair H^1(X, \mathbb{Z}) \to H^{1,0}(X) which do not obey Theorem 1.

Here is the solution. We define a Hermitian inner product on H^{1,0}(X) by

\langle \alpha, \beta \rangle = \frac{1}{2 \pi i} \int_X \overline{\alpha} \wedge \beta.

This is easily shown to be positive definite. We note that

\langle F^* \alpha,\ F^* \beta \rangle =(1/2 \pi i) \int_X F^*(\overline{\alpha} \wedge \beta) =
q (1/2 \pi i) \int_X \overline{\alpha} \wedge \beta = q \langle \alpha, \beta \rangle

where the middle equality is because F acts by q on H_{DR}^2(X, \mathbb{C}).

So q^{-1/2} F^* is a unitary operator on H^{1,0}(X)! The eigenvalues of a unitary operator have norm 1, and this completes the proof.

* These ideas appear in print in the papers of Grothendieck, Kleiman and Serre which I link above. But Grothendieck and Kleiman both imply that what they are recording was common knowledge already.

** Let X be the genus two curve y^2=x^5-1. This curve has an automorphic \sigma of order 5; multiplying x by a primitive fifth root of one. The action of \sigma on H^1(X) has eigenvalues \zeta, \zeta^2, \zeta^3 and \zeta^4, where \zeta is a primitive fifth root of 1. Then 1 + \sigma^* preserves the splitting H^1(X, \mathbb{C}) = H^{1,0}(X) \oplus H^{0,1}(X) and the lattice H^1(X, \mathbb{Z}), but the eigenvalues of 1+\sigma^* are 1+\zeta^i, for 1 \leq i \leq 4, and these do not all have the same norm.

8 thoughts on “Characteristic zero analogues of the Weil conjectures: Curves”

  1. the curves of degree 2 or higher,is decoveried through the strings
    vibrating in frequency differents;when the universe of 4-dimension,coupled minimally the time as 4-imaginary components(como the 32 -componrents od the majorana,2-spinors.the time component place two rotations by 720 degrees and torsion the curvature tensorXac,bd-X*ac,db+X”ca,-db.the we will obtain the
    holes in the spacetime that are the vibrations of the spacetime,or
    frequency only one-then the particles aren’t reals,but pulsations that
    go from zero to infinity and -1 to -infinity
    then the zeros of the zeta of riemann are given the holes of the strings
    vibrating in its minimum and maximum points..reflecting the infinities dimensions of spacetimes extra that are symmetry of cpt and mirrors
    that are holographycs

  2. Great post!

    Quick question: does Theorem 1 generalise how you’d expect, saying that any algebraic endomorphism acts on H^i(X) with weight i/2? And similarly for possibly singular, noncompact X replacing H^i with H_c^i and having mixed weights less than or equal to i/2?

    Additionally, where did this come from in the characteristic 0 case? Surely it was known to Deligne before he wrote his articles on the Weil Conjectures? Did this motivate Grothendieck’s definition of motives, or was it the other way round?

    Sorry if I’m jumping the gun here!

  3. The questions you are asking (except for the ones about singular and noncompact varieties) are exactly the ones I plan to take up in the following posts. Some brief answers for now.

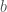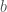    The higher dimensional case is not as simple as you hope. Think about a product of two elliptic curves, E_1 \times E_2, and the endomorphism that rescales one factor by a and the other by b. The action on H^1 has two eigenvalues of a and two of b. The correct statement will be in the next post.

    Serre seems to be the first person to have made these observations in print, in his 1960 paper “Analogues kählériens de certaines conjectures de Weil.” That is pre-Deligne. But I think this material, especially in the curves case, may have been folklore long before that.

    And, yes, I plan to get to motives eventually. The expository route I plan to take is to explain all the arguments first without the motivic terminology, and then explain how motives simplify the presentation. That is the historic order of publication. I imagine that it is the historic order of discovery, although I can not be certain what Grothendieck and others might have known but not written down.

  4. Thanks, that’s great. Looking forward to the next post!

    You say that the material (especially Theorem 1) “may have been folklore long before that”. Do you know of any reference for this? It would be great to know who realised this first!

  5. Pingback: The Weil conjectures and the problem of coefficients « Secret Blogging Seminar ~
  6. Pingback: Motive-ating the Weil Conjecture Proof « Secret Blogging Seminar ~

Comments are closed.