A number of blogs I read are arguing about a paradox, posed by tumblr blogger perversesheaf. Here is my attempt to explain what the paradox says.
Suppose that a drug company wishes to create evidence that a drug is beneficial, when in fact its effect is completely random. To be concrete, we’ll say that the drug has either positive or negative effect for each patient, each with probability . The drug company commits in advance that they will state exactly what their procedure will be, including their procedure for when to stop tasks, and that they will release all of their data. Nonetheless, they can guarantee that a Bayesian analyst with a somewhat reasonable prior will come to hold a strong belief that the drug does some good. Below the fold, I’ll explain how they do this, and think about whether I care.
To be concrete, let’s suppose that the drug company knows that the analyst begins with a uniform prior on the drug’s efficacy: she thinks it is equally likely to be any real number between and
. And the drug company’s goal is to get her to hold a greater than
percent belief that the drug’s benefit is greater than
.
The drug company chooses (and announces!) the following procedure: They will continue to run patients, one at a time, until a point where they have run patients and at least
have benefited. This will eventually happen with probability
. At this point, they stop the study and release all the data. If the analyst updates on this, she will believe that the drug has effectiveness
with a probability that is roughly a bell curve around
and standard deviation
. (I didn’t check the constants here, but this is definitely the right form for the answer and, if the constants are wrong then just change
to
.) In particular, the analyst would be willing to bet at 19 to 1 odds that the drug does some good.
If we think that the key to this error is that the length of the experiment is allowed to be infinite, perversesheaf gives some practical numbers based on simulation, which I have also checked in my own simulations. If the experiment is cut off after patients, or when
are helped, which ever comes first, then it is the latter situation about 30% of the time.
I mostly want to open this up for discussion, but here are some quick points I noticed:
The uniform prior isn’t important here. As long as the analyst starts out with some positive probability assigned to the whole interval
for some
, you get similar results.
As Reginald Reagan points out, the analyst rarely thinks the drug is very good.
To state the last point in a different manner, if the drug was even mildly harmful (say it helped 45% of patients and harmed 55%), this problem doesn’t occur. With those numbers, I ran a simulation and found that only 6 out of 100 analysts were fooled. Moreover, in the limit as the simulation goes to
, the fraction of analysts who are fooled will stay finite: If a random walk is biased towards
, the odds that it will be greater than
, let alone greater than
, drop off exponentially.
Normally, I’d like to think a bit more about the question before saying something, but I am getting tired and I want to put up this post for one very key reason: Tumblr is an absurd awful interface for conversations. So, I am hoping that if I get a conversation started here, maybe we will be able to actually talk about it usefully.
It’s a straw man… Drug trials do not enroll patients sequentially until the person running the study says “enough”. The number of patients to be in the study is fixed before the study is opened.
Wow. I talked to someone about this. I’m dead wrong. There are so-called Bayesian trials. Amazing. How can the statisticians in charge of validating clinical trial designs not know that a random walk will almost always contain multi-sigma deviations from the initial expected values along the path?
Final comment (I promise): Apparently the FDA rules are that Bayesian design is only used in phase I/II, not phase III – so any result from a Bayesian design must undergo confirmation by an independent, non-Bayesian study (informed by the Bayesian result). So not a problem after all.
The standard response from a “radical Bayesian” point of view, which I happen to think is correct here, is that the hypothetical Bayesian here is not updating on all of the available evidence, namely exactly the argument you’ve presented.
The error is exactly that the rule by which the patients were chosen affects the probabilities. The information that you learned is not the identity of the people on whom the treatment succeeded, but the stopping time . Accordingly, the probability of seeing the result is not “the odds that if we test
. Accordingly, the probability of seeing the result is not “the odds that if we test  patients, the treatment will succeed for
patients, the treatment will succeed for  of them”, but “the odds that we will stop at time
of them”, but “the odds that we will stop at time  “. I’m not sure how the distribution of stopping times depends on the probability, but my intuition is that there should be a big difference between the distribution of the stopping times in the 50/50 and 55/45 cases, so the Bayesian agent is highly unlikely to believe the efficacy is 0.55.
“. I’m not sure how the distribution of stopping times depends on the probability, but my intuition is that there should be a big difference between the distribution of the stopping times in the 50/50 and 55/45 cases, so the Bayesian agent is highly unlikely to believe the efficacy is 0.55.
Qiaochu: But in what sense isn’t she? I’m hardly an expert, but one thing that I have always heard emphasized about Bayesianism is that you update on the probability of the specific sequence of events that occured, not on some larger collection of events you might lump it into. See, for example Beautiful Probability and the more formal sources quoted within. And the probability that good results would be reported really is peaked tightly around
good results would be reported really is peaked tightly around  .
.
I can imagine one possible answer: You might be skeptical that the drug companies halting procedure is truly as claimed. You might suspect that, rather, they did some unreported initial trials which lead them to believe that the drugs efficacy was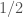 , and only then announced this protocol. (If the drugs efficacy was
, and only then announced this protocol. (If the drugs efficacy was  , then they would have announced a protocol of halting at
, then they would have announced a protocol of halting at  instead.) But this doesn’t seem to be what you are suggesting.
instead.) But this doesn’t seem to be what you are suggesting.
Alex: I was more interested in whether this is a valid criticism of Bayesianism than of the FDA. But the practical issue also interests me. There is a big problem here. If the evidence is overwhelming (in either direction) we want to be able to stop the trial early and act on the knowledge we’ve gained. I think that figuring out how to gain the most knowledge with the fewest patients wasted in inferior treatments is a fascinating problem.
At the moment, my practical suggestion for the FDA would be to only allow Bayesian evidence that a trial is significantly better than the status quo. After all, none of these issues arise if we allow the study to stop after it reaches successes: A drug with efficacy
successes: A drug with efficacy  will, with high probability, never do so. (Tweak the numbers until they come out right; I didn’t actually work out how unlikely it is for a random walk to get that high.) It is only aiming for
will, with high probability, never do so. (Tweak the numbers until they come out right; I didn’t actually work out how unlikely it is for a random walk to get that high.) It is only aiming for  that causes the problem.
that causes the problem.
@Lior As I understand it, the relevant probability to multiply by in Bayesian updating is the probability of the precise list of cures and non-cures, that is to say, . It is just a fact that, for any
. It is just a fact that, for any  , this function is concentrated almost entirely on the right half of
, this function is concentrated almost entirely on the right half of ![[0,1]](https://s0.wp.com/latex.php?latex=%5B0%2C1%5D&bg=ffffff&fg=444444&s=0&c=20201002) .
.
I think the solution has to be that instead of updating based on the likelihood of this observation, you update on the likelihood of all observations in this class (which is 1, so no change). It’s a lot like the old “I tested 100 SNPs and one was significant p<.01".
Making this rigorous is hard.
@David: It may be that this is how the FDA does Bayesian updating, but it’s the wrong way to do it. The correct way to update is , where $\textrm{data}$ is what you observed. You observed two things: 1. The stopping time is
, where $\textrm{data}$ is what you observed. You observed two things: 1. The stopping time is  2. the cures and non-cures up to times
2. the cures and non-cures up to times  . You are updating on 2 but ignoring 1 despite the fact that the stopping time
. You are updating on 2 but ignoring 1 despite the fact that the stopping time  is itself an observation, and that the distribution of
is itself an observation, and that the distribution of  will be heavily weighted toward short times if
will be heavily weighted toward short times if 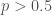 and longer times if
and longer times if  exactly. I have no intuition on the distribution of $N$ when
exactly. I have no intuition on the distribution of $N$ when  , but note that in that case with positive probability you never stop.
, but note that in that case with positive probability you never stop.
I assert the following:
A. (formal claim) Conditioned on observation 1, observation 2 gives no information on $p$ (because one we know $N$, we know the number of cures and non-cures and their distribution is independent of $p$). In particular, updating on both 1 and 2 is equivalent to updating on 1.
B. (informal belief) Updating on 1 will likely cause the agent to behave correctly, because it is highly unlikely that you'll see the desired deviation in a time as short as you'd see when the treatment works.
This would fool Lubos Motl, but not someone who understands Bayesian statistics.
I do not think Lior’s suggestion works, as knowledge of the stopping time $N$ is already inherent in the data. Let $N$ represent the knowledge that we have stopped after $N$ trials. Consider:
$p(\theta| N, y) \propto p(N,y|theta) p(\theta).$
Further, $p(N,y|theta)=p(N| y, \theta) p(y|\theta)= p(y|\theta)$, as $p(N| y, \theta)=1$: once we know $y$, we know $N$. So applying Bayes’ rule here reduces to the original inference, where we did not condition on $N$.
Further, I am intrigued by Qiaochu’s suggestion, but wonder how it might be formalized. It seems we just run into similar problems.
@Sheaf: On further thought, I realize that the problem is exactly that if the stopping time is infinite with positive probability. As you say, seeing the sequence is equivalent to knowing
the stopping time is infinite with positive probability. As you say, seeing the sequence is equivalent to knowing  , so the Bayesian agent makes the same update whether he updates on
, so the Bayesian agent makes the same update whether he updates on  or on the sequence.
or on the sequence.
However, updating on has the pedagogical advantage of clarifying what to do when
has the pedagogical advantage of clarifying what to do when  . Lets add an implicit assumption: when $p<0.5$, the results of the study are only reported if the desired fluctuation actually occurs. This means that the probability of the study having size
. Lets add an implicit assumption: when $p<0.5$, the results of the study are only reported if the desired fluctuation actually occurs. This means that the probability of the study having size  is not the probability of stopping at that time, but the probability of stopping at that time conditioned on having stopped at all. So, in that range you need to divide the probability of the data given the parameter (as you say, either the odds of stopping at time
is not the probability of stopping at that time, but the probability of stopping at that time conditioned on having stopped at all. So, in that range you need to divide the probability of the data given the parameter (as you say, either the odds of stopping at time  or the product from David’s post #7) by the odds of stopping at all. This will make the function less concentrated on
or the product from David’s post #7) by the odds of stopping at all. This will make the function less concentrated on 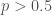 .
.
@Lior But the stopping time is inherent in the series of events. The drug company announced their halting algorithm at the start. Possibly, the Bayesian’s failure is not updating on the drug companies choice of algorithm, but once they have announced the algorithm, the stopping time is no additional data beyond the cures.
Reginald Reagan suggests that the statistician should start with distribution strongly peaked near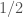 , because why else would the drug company use this protocol. Maybe that’s right, but I have the vague feeling that there are game theoretic issues associated to updating your views in response to something an adversary says.
, because why else would the drug company use this protocol. Maybe that’s right, but I have the vague feeling that there are game theoretic issues associated to updating your views in response to something an adversary says.
@Daniel Hi! I guess what is puzzling me is that Bayesian’s tend to boast that the great advantage of their method is that you don’t have to figure out what which events to lump together, you just use the literal probability that you see the observations you’ve seen. I think this handles the 100 SNP’s case fine, as long as the experimenter reports the 99 failures. But I am puzzled about this variant.
@David: yes, the stopping time doesn’t give information beyond the cures, but conversely the cures give no information beyond the stopping time: the likelihood ratio is the same in both cases.
is the same in both cases.
The problem in the analysis is that when the probability $P(data|p)$ is not the the number given in your post #7 but rather that number divided by the probability that the experiment ends.
the probability $P(data|p)$ is not the the number given in your post #7 but rather that number divided by the probability that the experiment ends.
Sorry; the likelihood ratio is $latex \frac{P(\mathrm{data}|p)}{P(\mathrm{data})}.
@Lior Oh, I see what you are getting at now! Thanks for your patience. I’ll write a bit more in a bit.
Here is a simpler example to help me think about this. Suppose that the announce protocol is to halt as soon as there is one more cure than non-cure, and the observation is that the halt occurs after 3 cures and 2. Naively, I would say that the odds ratio should be . However, the probability that we halt AT ALL is
. However, the probability that we halt AT ALL is  . (Proof to follow.) So you would say that the correct formula is
. (Proof to follow.) So you would say that the correct formula is  .
.
In this picture, I plotted the naive formula in blue and the corrected version in yellow; they take the same value for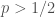 , which is green. As you can see, this correction factor increases things for
, which is green. As you can see, this correction factor increases things for  . I need to think a bit about what happens if we stop the sum at a finite but very large value. And, of course, it would be very fun to think about estimating the sum for the stopping rule we actually care about.
. I need to think a bit about what happens if we stop the sum at a finite but very large value. And, of course, it would be very fun to think about estimating the sum for the stopping rule we actually care about.
For the curious: Let the random walk run forever, and let be the probability that we eventually reach position
be the probability that we eventually reach position  . We have
. We have  . The general solution of this recurrence is
. The general solution of this recurrence is  . Plugging in the boundary conditions
. Plugging in the boundary conditions  and
and  , we see that
, we see that 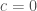 and
and  . So the probability of ever reaching position
. So the probability of ever reaching position  is
is  . I quoted this result for
. I quoted this result for  .
.
Two reservations I still have: (1) This seems to contradict McKay’s argument in Section 37.2 here. Of course, this could just mean McKay is wrong. (I found this link from Yudkowsky’s essay here, but I am less bothered by the notion that Yudkowsky is wrong.) (2) I still need to think about how to adapt this argument to the large but finite halting: What if I insist that I will stop after steps no matter what?
steps no matter what?
More thinking made me realize that my claim that we need to normalize wasn’t right, and your initial formula in #7 was correct — the problem was with the interpretation.
We are assuming that you (the Bayesian agent) know in advance that there will be an experiment, and then you hear about the result. Then there is no need to normalize, since the fact that the experiment terminated is part of the observation. However, now we shouldn’t feel bad that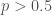 is favoured: the fact that the experiment terminated at all is evidence for that result.
is favoured: the fact that the experiment terminated at all is evidence for that result.
I’m trying to formulate may thoughts in the case where you don’t know about the experiment in advance (so that the drug company is free to leave negative and null experiments unreported).
Glad to hear that. I also came to the conclusion last night that we didn’t need to normalize.
I’m not as bothered by the situation where the experiment isn’t announced in advance, because we already understand that interpretation in the presence of unreported results is a mess. (That’s the difference between a pure and an applied mathematician — as soon as I have a good understanding of why the problem is unsolvable, I am satisfied. :) )
I hope I’m not missing something from the preceding comment thread, but…
Suppose we know going in that the p>=.5. Then the fact that the experiment terminates isn’t evidence. This brings back the paradox. If we don’t want to transform our observation into something more manageable, then it seems we do need to normalize.
Because the probability that a patient in our sample was cured is not the same as the probability that a patient in general was cured.
Let’s take a really easy problem. We’re trying to determine if dogs are small. So we go down to the chihuahua shop and buy a bunch of dogs and discover that they are small. Far more often than chance allows. And we conclude dogs are small. Clearly we are doing something wrong here. The chihuahua shop is not a random sample of dogs.
Similarly, the patients in our sample were drawn from the space of possible patients in a way that was more likely to include cures than harms.
If we can calculate how much more likely a cure is to be included, (and it should be possible, I just don’t care to attempt it at this hour) then we should be able to convert the probability of observing a specific cure to the probability of a cure in general. I think that should get us out of this mess. It’s just that the calculation is so ugly that updating on classes or on N starts to look appealing by comparison.
I just came back to this and looked at the thread of comments. Now that I’ve had some time to digest I’ll add my own $.02 (violating my promise from a few days ago :D).
Consider an assumed distribution D for the drug’s benefit on a given patient. When coupled with a stopping rule (e.g. stop enrollment and experiment when cumulative benefit has p-value < .01), the assumed single patient distribution D induces an assumed distribution S of stopping times.
I don't know how to compute S in closed form even for a Gaussian or binary ansatz for D, but I can easily compute S by simulation. Now we run trials and iteratively update our prior S with newly realized stopping times using standard Bayes.
Not sure if we can go back from our fully bayesian S to a pdf for single patient benefit D in a unique way, though. There might be a degeneracy in computing D(S), e.g. in the gaussian case there may be parameters {mu1, sig1} and {mu2, sig2} such that D(mu1, sig1) and D(mu2, sig2) give the same stopping time distribution S or close to it. My guess is that D S really is bijective, but if S(params) == S(D(params)) has flat directions in params space so that grad S in those directions is very small then the inversion won’t be reliable. Probably ok with a 1 or 2 parameter functional form for D, though.
Again, just my way of thinking about it.
That was “D(S) really is bijective”. Somehow my parens got dropped…
testing latex–$\theta$
Okay, so you guys are using images for latex? Not sure how to add images.
David said, “Reginald Reagan suggests that the statistician should start with distribution strongly peaked near 1/2, because why else would the drug company use this protocol. Maybe that’s right, but I have the vague feeling that there are game theoretic issues associated to updating your views in response to something an adversary says.”
I should clarify. First of all, I am _not_ suggesting you update on the drug company’s protocol. I’m assuming that they don’t have any more information about the drug than we do. If I thought they did know something more about the drug, then I _would_ update on their protocol, as you said, but that’s kind of leaving behind the thought experiment.
What I’m saying is, if our prior distribution is identical to our prior degrees of belief, we end up in one of two situations:
1. We don’t think the drug company can make us believe theta > 1/2
2. Our prior dist for theta is strongly peaked near 1/2
The significance of this is that, in neither case do we think of the thought experiment in the OP as a reason not to do a Bayesian analysis.
The math backing this up was too much to put in a comment, so here it is as a pdf:
https://drive.google.com/file/d/0B6198rcSwqpyb0FseGlkZUJWcVE/view?usp=sharing
some errata, since I can’t update the pdf right now:
Last sentence of the intro should match the comment
Below the disjunction sign and summation sign in section one, I wrote “i=ceil(N/2+sqrt(N))” where I meant “N=1”. Long story.
@Reginald Reagan: That’s an interesting point, but it doesn’t feel like the kind of guarantee I want from a statistical procedure when the data is being generated by an intelligent being. I want to know that, whatever the true value of , my method will come pretty close to detecting it.
, my method will come pretty close to detecting it.
By the way, it occurs to me that the drug example may not be the best story to consider wrapping around this problem, because it really shouldn’t matter if a drug is equal to placebo or better. As an alternate story, suppose the experimenter is Chien-Shiung Wu trying to demonstrate parity violation in weak interactions. Now any nonzero effect, in either direction, is Nobel prize material; we really do care about whether the value is exactly
better. As an alternate story, suppose the experimenter is Chien-Shiung Wu trying to demonstrate parity violation in weak interactions. Now any nonzero effect, in either direction, is Nobel prize material; we really do care about whether the value is exactly  or not. Are you comfortable analyzing that data by this method ?
or not. Are you comfortable analyzing that data by this method ?
If we don’t already know that parity is violated, then I have nonzero prior belief that the value is exactly .5. If I do the analysis using a prior that matches this prior belief, then I won’t be tricked by stopping rules. (maybe. Haven’t proved anything, just done simulations for one particular prior.)
I am always comfortable using a Bayesian analysis with a prior that matches my prior belief. In practice this is hard and I use frequentist analyses a lot because I don’t feel like dealing with prior specification. But what I’m mainly concerned with is whether Bayesianism is correct.
All this example shows me is that there are certain experimental designs where you have to include prior information that you can normally get away with leaving out (specifically, the possibility of the parameter being exactly .5). Nobody says that systems with significant air resistance disprove Newtonian physics, just because it’s common practice to leave out air resistance.
What does worry me, though, is this possibility:
Suppose I have a prior that puts nonzero probability on p=1/2. I’m worried you can construct a stopping rule such that, as p approaches 1/2 without becoming equal to it, the probability that I conclude that p=1/2 approaches 1.
Or, worse, maybe there’s a neighborhood around p=1/2 in which the stopping rule guarantees that I’ll conclude p=1/2.
In fact, the more I think about it, the more strongly I’m driven to conjecture that this is the case. So I don’t really believe that putting nonzero prior probability on p=1/2 protects Bayesian analysis from stopping rules.
Actually, I don’t think that is a risk, due to the weak law of large numbers. If the true probability is , then there is a positive probability (namely
, then there is a positive probability (namely  ) that the data will NEVER have more successes than failures. And, as
) that the data will NEVER have more successes than failures. And, as  gets large, with probability approaching
gets large, with probability approaching 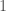 the fraction of successes will be
the fraction of successes will be  . Eventually, that
. Eventually, that  will be larger than
will be larger than  , so the odds ratio will be peaked well away from
, so the odds ratio will be peaked well away from 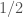 .
.
@Reginald Reagan I see what you are getting at now, and I think you have a good point. If it really is absurd to think that is exactly
is exactly 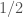 (or is so close to
(or is so close to 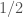 that a reasonable amount of time would have high probability of the stopping protocol mattering), then there is no problem. If it isn’t absurd, then the problem is that the starting prior doesn’t match the publicly available knowledge.
that a reasonable amount of time would have high probability of the stopping protocol mattering), then there is no problem. If it isn’t absurd, then the problem is that the starting prior doesn’t match the publicly available knowledge.
This maybe makes a good case for the rule of thumb “report odds ratios, not posterior priors”. If the statistician simply reports the formula , then people who know the context of the experiment can decide how important a very skinny peak slightly to the right of
, then people who know the context of the experiment can decide how important a very skinny peak slightly to the right of 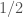 matters.
matters.
Suppose I have a prior that puts nonzero probability on p=1/2. I’m worried you can construct a stopping rule such that, as p approaches 1/2 without becoming equal to it, the probability that I conclude that p=1/2 approaches 1.