Since Scott broached the topic I want to talk a little bit about higher (and lower!) dimensional analogues of planar algebras. This will be somewhat vague, but will end with some nice pictures.
Let’s first think about categories. We all know and love categories. Furthermore, since categories are functions between things we all know how to draw pictures of categories: they’re just the same “function machine” pictures we’ve been seeing from precalculus. For example, if X, Y and Z are objects and F is in Hom(X,Y) and G is in Hom(Y,Z) we draw:
Let’s reinterprate this picture a bit. What we’re doing is plugging F and G into the holes in this picture:
We call pictures like this a “linear arc diagram.” What structure do linear arc diagrams have? Rather than plugging in morphisms F and G into those holes we could instead plug in another linear arc diagram (as long as the boundary labels agreed). Thus, linear arc diagrams have the structure of a colored operad. Furthermore, any category with objects in a specified label set is an algebra over this colored operad. (This means exactly that we can fill morphisms into the holes and get a new morphism out (their composition).)
Ok, let’s move up a dimension. Now suppose we have a 2-category. Most people like to think of a 2-category as having objects, 1-morphisms, and 2-morphisms. (Actually, most people don’t like to think of 2-categories at all…) I prefer to think of a 2-category as a generalization of a monoidal category. Think about bimodules to get the right idea. Here’s the correspondence:
| Objects | Labels |
| Morphisms | Objects |
| Composition of morphisms | Tensor product over the label |
| 2-morphisms | Morphisms |
| Vertical composition of 2-morphisms | Composition of morphisms |
| Horizontal composition of 2-morphisms | Tensor product of morphisms |
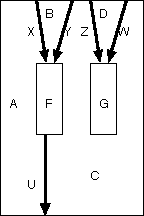
Okay, now that I have something that looks like a monoidal category I can use the usual Penrose-Rehsetikhin-Turaev-Joyal-Street picture calculus. For example we have the following diagram representing the tensor product of and
.
But we can again erase all the morphisms and think of these pictures as a colored operad! I’ll call it the operad of rectangular planar arc diagrams. A 2-category is an algebra over this operad. (I think really weak notions of 2-categories still fit in this framework, like quasi-2-categories, but I get confused whenever I try to think about it.)
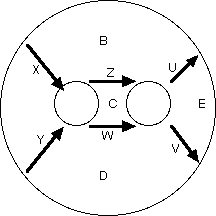
Ok, what if the 2-category has duals? Well then we can pull strands which go down into strands which go up. This means the picture is a lot more symmetric. The boxes no longer need to have a top and a bottom where the strands come out, we can instead just turn all the boxes into circles! So a 2-category with duals is an algebra over the operad of circular planar arc diagrams (or “spaghetti and meatball diagrams”):
You can recover Jones’s notion of a Planar algebra (which is tweeked for applications to subfactors) by considering the case where you only allow two colors for regions and only have one allowed label for an arrow sitting between two given regions. In topology you usually only allow one color for regions but often allow many colors for arrows. (For more details see page 3 of Scott’s slides, page 22 of Dror’s paper, or if you have more time read the original.)
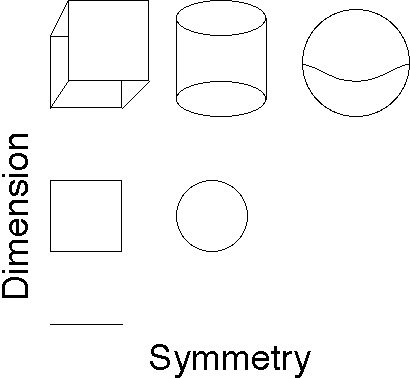
What happens in 3-dimensions? Well we could use rectangular prisms and get a very weak notion of a 3-category. If this is a little more symmetrical (has some notion of duals) then we have cylinders (this is the theory of canopolises). If there is even more symmetry (like in the Khovanov homology theory that Scott and Kevin Walker are chasing), then you should be able to replace the cylinders with spheres (i.e. meatball and lasagna diagrams).
All of this fits nicely into a Baez-style periodic table:
The traditional n-category theory perspective is to look at the left-most column as fundamental, and think of moving further right as adding more duals. This is how Lauda-Pfeiffer think of Khovanov homology, for example. Those of us infused with the Jones seminar propaganda tend to think of the rightmost column as the most important since it most clearly exhibits all the structure present.
Moving directly up in the picture is an “enrichment.” So you can think of 2-categories as categories enriched over categories. Similarly you can think of canopolises as planar algebras enriched over categories. Scott’s last post explains why the usual difficulty of weak vs. strong re-appears in the canopolis perspective. Moving right requires having more duals. Moving left is breaking symmetry.
I’d wanted to share a little propaganda about why planar algebras can be better than 2-categories, but I think I’m too tired for that now. Hopefully Scott or I will return to this at some point.
(p.s. A lot of the ideas in Scott and my posts come from stuff that have bounced off lots of people in Berkeley, in particular Ari Nieh and Chris Schommer-Pries have added a lot to our understanding of this picture. Furthermore, although as a rule of thumb it is usually Ari or Scott who coins a slightly goofy name for pictures, “lasagna” was my term.)
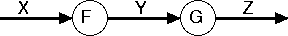
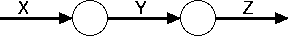
Interesting! Makes you wonder why these operads rather than others.
Regarding ‘lasagna’, in 2001 in what was probably the first philosophical talk on n-categories, feeling the limitations of spaghetti, I resorted to ‘fettucini’. Quite possibly pasta has more to offer yet.
Isn’t one of the points of the box approach that pulling strands from down to up requires introducing the corresponding dual entity? If you’re allowed to smoothly slide your strands around a circle with no privileged direction, does this mean you’re restricted to self-dual entities?
There was a point in Scott’s talk that kind of confused me. He introduces Khovanov homology using some kind of operad whose objects are links embedded in 3-spheres, and whose morphisms are lasagna embedded in punctured 4-balls. Then Khovanov homology is a distinguished algebra over this structure (vector spaces for links, multiplication for lasagna). Somehow, he moves to a lasagna setting one dimension down, and it looks like the lasagna here is a representation of the lasagna above, but I couldn’t keep track of whether the lower lasagna encoded cobordisms or natural transformations between them. Any hints?
Incidentally, does anything interesting come out if you label your 3-morphisms by arbitrary embeddings of closed 2-manifolds in 3-space rather than just spheres? I’m speculating wildly here, but it might be worthwhile to put something like CFTs on the 2-manifolds.
David: In the planar algebra picture you denote duals by the orientation on the curve, and there should be “joints” that allow you to switch orientations. Of course, those joints cancelling out is exactly the “zig-zag” identity.
In the canopolis picture I’m really not sure what the proper analogue is.
Non-self-dual objects (i.e 1-morphisms) correspond to using oriented spaghetti, while if you use unoriented spaghetti you end up forcing everything to be self-dual. In Jones’s context since everything is a C*-algebra, things are all self-dual so he doesn’t need to use oriented spaghetti.
So are spherical n-categories just your right hand column? And is there ever any call to be in the halfway house of cans?
Spherical categories is a slightly different notion. In 2-dimensions, just a pivotalness is enough to go to the disc planar algebra picture. Sphericalness says that for 0-boxes (ones with no free strands on the edges) you can think of them as living on a 2-sphere instead of the 2-disc. So sphericalness is slightly stronger than the rightmost diagonal. Similarly in 3-dimensions you could require that when you have no strands your pictures live on the 3-sphere instead of the 3-ball.
intresting hmmmmmmm