A grammatical oddity

I’m going through a referee report (generally positive, yay!) on one of my papers, and I just figured out something about my grammar. When I see the phrase “Let x \in S …”, I say in my head “Let x, in S, …”. My referee apparently says “Let x be in S …”. As a result, I keep writing sentences like “Let x \in S obey x^2=1,” which the referee keeps changing to “Let x \in S with x^2=1.” On reflection, I take this pretty far, although I am not perfectly consistent about it. I am much more likely to write “We deduce that x lies in S,” than I am to write “We deduce that x \in S.”

There’s probably an interesting little linguistics paper waiting to be written on this sort of thing.

10 thoughts on “A grammatical oddity”

  1. The referee’s suggested change definitely doesn’t seem grammatical to me. I wonder whether LaTeX syntax has any influence on the usage of symbols. When you’re writing \in all the time it feels better to read the symbol as “in.”

    I can’t quite figure out how the referee would apply this consistantly. The phrase “Consider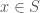 x \in S with x^2+1” doesn’t seem to have any obvious modification that let’s you read \in as “be in.”

  2. Both of your sentences seem correct to me, although

    Let $x \in S$ obey $x^2 = 1$

    is more in line with what I’d use. It might have something to do with LaTeX syntax.

    But at least you acknowledge the fact that mathematics, when read out, needs to form grammatical English sentences! That’s better than a lot of people who would write

    Let $x \in S, x^2 = 1$

    and not see what’s wrong with it.

  3. I think Don Knuth’s rule (in “Mathematical Writing,” with Tracy Larrabee and Paul Roberts) is that you should be able to substitute any mathematical expression (equation or otherwise) with “blech” and have it read correctly.

    So

    “let blech obey blech..”

    “consider blech with blech…”

    “we deduce that blech”

    “let blech obey blech”

    are all OK.

    Then again, I might not be remembering the rule correctly, so…

    blech.

  5. I think the referee is right on the grammar and wrong on the need to correct it, or it being his business to correct. That’s an editor’s job.

  6. My biggest question about mathematical grammer is the following. The sentence “Let $ x = 5$, then $ y =7$.” seems perfectly acceptable. But what about if we are using display math, so “Let $$x=5$$, then $$y=7$$.” Where do the comma and period go?

    If you put them inside the $$, then they will end up at the end of the math line, which looks ok, except when the equation gets too big at which point the period and comma look like strange out-of-place dots (think of the example where the equation is actually a commutative diagram). Another approach is to leave them out altogether and take the attitude that an equation comes with a punctuation at the end.

  7. Various professors while I was an undergrad insisted that periods and commas always had to go in, always at the end of the math line. Since then, the intersection of people I’ve talked about this with and of people who care about this seems to be heavily in favour of this solution, even if the punctuation sometimes does get a little lost.

    While leaving them out altogether seems reasonable, if you’re consistent about it, I think you’ll run into too many punctuation pedants who want it done the old-fashioned way.

  8. I’m actually one of the people who believes that putting punctuation is displayed equations is important.

    On the other hand, I’m of the opinion that commutative diagrams are not part of sentences, so they don’t need punctuation. Where this punctation stuff actually becomes awkward is when you use the environment “cases.” That one I’m not really sure what to do about.

  9. With regard to the original posting, my standard rule is to keep symbols out of sentences if ambiguity can occur. If symbols can be `spoken’ in different ways and you have a specific vocalization in mind then spell it out. So I would go for “Let $x$ be an element of the set $S$ with $x^2=1$.” Alternatively you could go for “Let $x$, in $S$, obey $x^2=1$” but is that really the way you would say it out loud? The reader is going to try to speak it in their head and surely it’s better if they’re using their brain-power to try to understand the maths rather than to try to parse the symbols.

    One of my bugbears is sentences of the form “So we see that $A=B$ satisfies condition Y.” where what is meant is that $A=B$ and both of these satisfy Y and _not_ that the *equation* $A=B$ satisfies Y. Ask yourself `What is the object of that sentence?’ As I say, an effort to make grammatically unambiguous sentences by the writer can make the reader’s job considerably easier.

    As for Ben’s comment about a commutative diagrams not being part of a sentence, I think that that depends on the construction. Consider these two cases.

    We now look at the following commutative diagram:
    [commutative diagram].

    Now look at the commutative diagram below.
    [commutative diagram]

    Is either more correct than the other? I’m not sure. Does either look better? I guess that’s a question of taste, though I don’t think I have a strong opinion either way.

  10. I probably think of it the way the referee mentioned here does. But that’s because of my logic training. = and \in are both relations, so they must be verbs. This is also the same reason it really bugs me to see people writing on the board and putting \forall x after the equation instead of before it where it obviously goes. I think of it not just as an abbreviation for English, but actually a mathematical term that has its own (more precise) grammar.

Comments are closed.