As you may have heard, we’re having a conference here at IAS on derived categories and algebraic geometry. Last night, at the banquet for said conference, some time after the discussion of how the derived algebraic geometers should start a blog called”The -Category Cafe,” I got some complaints from someone who will remain unnamed (though for convenience, let’s call him “Navid Zadler”) about the lack of talk-blogging thus far (and particularly that he was concerned his own talk would not be blogged).
So, to put his mind at ease, I thought would give a little update. Yesterday was sort of symplectic day (well, except Olivier Schiffman, but we can discuss him later) and featured a very nice talk by Denis Auroux, on homological mirror symmetry.
So, what is homological mirror symmetry? Well, if you believe Kontsevich, it’s an equivalence or the derived category of coherent sheaves on one projective Calabi-Yau variety and the Fukaya category of another.
When trying to find categories that are derived equivalent to coherent sheaves on a variety, there a very useful principle which seems to come up again and again: the variety itself is a subvariety of the “moduli space” of objects in the derived category of coherent sheaves.
This might sound deep, but it really just means that each point has a sheaf naturally associated to it: its structure sheaf. So, if you have a category which is derived equivalent to coherent sheaves on , the points of the variety are hiding in the space of objects in your derived category, and if your equivalence is interesting, they should be something reasonably natural. They should also be easy to spot because have a very specific form for their Ext algebra.
Theorem. If is smooth, then
.
So, if you have a category you think might be derived equivalent to a smooth variety, you’d better start looking for objects with Ext algebras of this form. It turns out that in the Fukaya category, there’s an obvious class of such objects: Special Lagrangian tori (with any flat unitary connection you want). Now assume we have “enough” of these, that is, that a generic point of our variety lies in a unique special Lagrangian torus.
This points to the Stominger-Yau-Zaslow picture of mirror symmetry, which says that we should consider smooth points of the moduli space of special Lagrangian tori in . There’s an open subset of
which fibers over this space, with special Lagrangian fibers.
On the other hand, we can take the tautological bundle over this space with fiber over a torus given by flat unitary connections on that torus (the dual torus). This can be thought of as a space of some objects in the Fukaya category with the right Ext algebras to be points. Thus, these should be points in the mirror dual.
It’s true that this is just an open subset, but that’s a good start.
Now, let’s get away from the Calabi-Yau assumption. Let be your favorite variety with effective canonical bundle (that is, which carry a holomorphic top form which vanishes on a divisor
.
Then homological mirror symmetry should associate a mirror dual to and “Fukaya” and “coherent” category to this dual which gives equivalences to the derived category of coherent sheaves and Fukaya category on
.
Unfortunately, this dual object isn’t a variety, but a variety with a superpotential. Specifically, you should take the SYZ dual of
, which is Calabi-Yau, and then you should use the divisor
to build a function
on this dual having to do with holomorphic disks with boundary on the Lagrangian torus passing through $D$. You should think of this as one object, which is some wacky generalization of the notion of a variety. So what are “coherent sheaves” on this variety? It turns out what you want is matrix factorizations of coherent sheaves on
with potential
. So for non-Calabi-Yaus, homological mirror symmetry conjectures that the Fukaya category is isomorphic to this category of matrix factorizations.
The actual topic of Auroux’s talk was the other side of mirror symmetry, which describes the derived category of coherent sheaves in turns of a Fukaya category on relative to the subvariety
, and the compatibility of this mirror symmetry with restriction functors to the coherent and Fukaya categories on
and
(which are Calabi-Yau). Unfortunately, this post is a little too long already, so you’ll just have to read the paper (I’ll give you a hint: like everything involving the Fukaya category, it seems reasonable, and then ends up being much harder than it has any right to be).
Hi Ben,
What’s the mirror of P^1?
Scott – Remember when I said that the canonical bundle should be effective?
One thing that I found interesting in Denis’s talk is that he explained why one needs this superpotential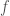 . Consider the Fukaya category of our original variety
. Consider the Fukaya category of our original variety  . If we have a Lagrangian L in
. If we have a Lagrangian L in  , then it may bound holomorphic disks which meet D. These disks will screw up our Fukaya category of X.
, then it may bound holomorphic disks which meet D. These disks will screw up our Fukaya category of X.
Specifically, the Fukaya category is an category with composition maps
category with composition maps  . These disks will introduce an
. These disks will introduce an  . In fact we will have
. In fact we will have  where
where  is a Lagrangian with a flat connection on the trivial line bundle over it. This function
is a Lagrangian with a flat connection on the trivial line bundle over it. This function  is given by an explicit formula. Continuing the analysis shows that
is given by an explicit formula. Continuing the analysis shows that  becomes 0 in the Fukaya category unless it is a critical point of the function
becomes 0 in the Fukaya category unless it is a critical point of the function 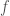 .
.
Now, above Ben explained how gives us a point in Y, the SYZ mirror dual of
gives us a point in Y, the SYZ mirror dual of  . So this analysis shows that we have a function
. So this analysis shows that we have a function  and should throw away the points of Y that are not critical points of the function f. A more refined analysis shows that we should look the category
and should throw away the points of Y that are not critical points of the function f. A more refined analysis shows that we should look the category  — namely for each singular fibre of f consider the category of sheaves mod perfect complexes. This will be the mirror of the Fukaya category of X. (By work of Orlov, this category is equivalent to one of matrix factorizations as Ben mentioned above.)
— namely for each singular fibre of f consider the category of sheaves mod perfect complexes. This will be the mirror of the Fukaya category of X. (By work of Orlov, this category is equivalent to one of matrix factorizations as Ben mentioned above.)
That’s odd. Page 5 of Ben-Zvi’s notes from the talk suggest that Denis is dealing with the Fano case, rather than general type, so P^1 should be the *only* curve that satisfies his conditions.
Anyway, I got as far as seeing that the mirror should be a punctured A^1, with some extra structure, but then I got lost in symplectic land.
I think that Ben made a mistake in the post. O(D) should be the anticanonical bundle.
The case of P^1 can be analyzed as follows. First D = north pole union south pole, since the canonical bundle is O(-2). So X – D admits a Lagrangian torus fibration, namely take the map X-D -> (0,1) (by horizontal sections of the sphere — also known as the moment map for the S^1 action). Then you look at the dual torus fibration which is isomorphic to an anulus in C (I think). Now, you need to find the superpotential f : C^x -> C. I suspect that it is z -> z + z^{-1}. I guess there are two singular fibres of this map (both double pts).
Some more instructive examples are given in Denis’ paper: 0706.3207