The Witt group, or the cohomology of the periodic table of n-categories

A very popular topic at the Modular Categories conference was the a generalization of the Witt group which is being developed by Davydov, Mueger, Nikshych, and Ostrik. What is this Witt group? Well it’s the simplest case of the cohomology of the periodic table of n-categories!

In this post I want to explain the definition of this cohomology theory and explain why it generalizes the classical Witt group.

First recall the Baez-Dolan periodic table.

Periodic Table

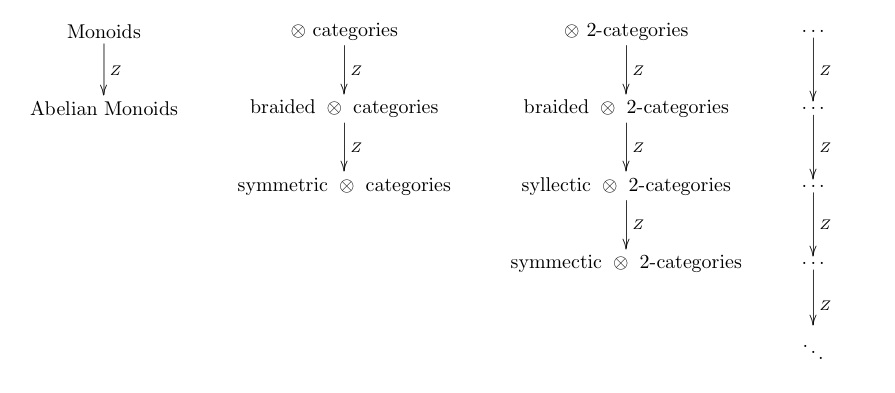
Periodic Table

Here all the functors are the generalized “center” construction defined in HDA-1. In the first column, the center means exactly what you think it means. In the second column the first arrow, which we’ll call Z_1, is the Drinfel’d center, while the second arrow is the Mueger center.

A result of Mueger’s says that under some niceness conditions Z_2(Z_1(C)) is automatically just vector spaces! Hence the second column is a complex. The natural thing to do is to take homology. If you restrict your attention to fusion categories (which have duals, are semisimple, and have finitely many simple objects) of non-zero dimension, then the kernel of Z_2 is exactly modular categories. So what you’re doing is taking all modular categories (which form a monoid under external tensor product) modulo those modular tensor categories which are Drinfel’d centers. A priori this only gives you a monoid, but Davydov, Mueger, Nikshych, and Ostrik prove that it is a group.

What about the other columns? I think Kitaev mentioned in passing in his talk that the other columns also form complexes. But I’m a little confused about why. In particular there’s something fishy going on somewhere. You can continue the periodic table downward past the diagonal, but it stablizes. In particular, if you look at Z^2 in that region you get the identity instead of the functor sending everything to vector spaces. Anyone know what’s going on? Mueger’s paper mentions an analogue (due to Baez) in the 1st column where you extend the table upwards by one row. In the first column this gives you sets where the center becomes “the monoid of all endomorphisms.” What’s the homology there? We could also extend the other columns upwards. Then the second column would start with categories, and Z_0 would be the monoidal category of all endofunctors. Is Z_1(Z_0(C)) always vector spaces? If so, why? Can you extend this picture leftwards by looking at (-1)-categories?

Enough questions that I can’t answer, let’s go to one I can answer: “Why is this called the Witt group?” Well, one nice class of tractable examples of tensor categories are the pointed tensor categories (this means that V \otimes V^* \cong \mathbf{1} for every V). Any braided pointed fusion category comes from an abelian group with a bilinear form. The abelian group is the Grothendieck group, and the bilinear form tells you by which scalar the braiding acts on the object V \otimes W = W \otimes V. (You should think of this as a kind of strictification.) Modularity becomes the condition that the bilinear form is nondegenerate, while Drinfel’d doubles consist of precisely the hyperbolic spaces. Hence the “Witt group” restricted to the pointed case is nothing other than the classical Witt group.

10 thoughts on “The Witt group, or the cohomology of the periodic table of n-categories”

  2. Z certainly passes between equivalent (n-)categories in the stable range, but I don’t see why Z is necessarily the identity functor. You should be able to embed everything as infinity-categories with certain truncations and get the same answer. As far as I can tell, you’re taking E_n Hochschild cohomology for successive n.

    By the way, \mathbb{1} is famously badly behaved. I usually use \mathbf{1}.

  3. Maybe I should clarify. The notion of center changes depending on your source category, and once you hit the stable range, it maps everything to the trivial object. In particular, if you take the “abelian monoid center” you will typically get a very different result than if you take the “associative monoid center” of a monoid that happens to be abelian. This is a bit easier to see in higher categorical settings, where commutativity is an extra structure rather than a property.

    Standard references (all available online): A preprint from last year by Ben-Zvi, Francis, Nadler. Also, material from Lurie’s DAG and HTT.

  4. Thanks Scott!

    So what’s the homology at the monoid spot. Extending the table upward you have Finite Sets -> Finite Rank Monoids -> Commutative Finite Rank Monoids where the first functor is look at all endomorphisms and the second functor is the usual center. (Or maybe I should be requiring some sort of duals? In which case perhaps monoid should be replaced by group?) So we’re looking at finite rank monoids with no center modulo the endomorphisms of sets. This doesn’t look like anything I’ve seen before. How do you express it in terms of some sort of Hochshild homology?

  5. Concerning your second question, extending one row up means considering E_0-algebras, which are just pointed objects. This is because the nth space in the E_0 operad is homotopy equivalent to configurations of n distinct points in R^0. Taking E_0 Hochschild cohomology amounts to taking pointed endomorphisms. If you’re working with vector spaces, the E_1 center is then the center of a matrix ring.

    I think both (-1)-categories are pointed, and taking the E_0-center takes both to \Delta^0.

    [Edit: Upon further reflection, I’m pretty sure the empty (-1)-category \Delta^{-1} is not pointed.]

  6. I really think you should use monoids instead of groups, since the abelianness of S_2 would make the sequence no longer a complex. I’m a little confused about taking the homology of the complex, and I think it’s because I don’t know what sort of equivalence relation you want to use when you say “modulo”.

    If O is an operad, the O-Hochschild cohomology (aka O-center) of an O-algebra A is the A-O module homomorphisms from A to A (this should be viewed as an object in your category). The O-Hochschild homology is given by tensoring with the universal enveloping algebra of A. This is all in some sort of derived setting. There is a conjecture of Kontsevich asserting that the E_n center of an E_n-algebra (in some symmetric category which I think is unspecified) has an E_{n+1}-algebra structure.

    [Edit: I should have said, “tensoring A with itself over the universal enveloping algebra.”]

  7. Surely we can agree that in the second column, if we consider categories which happen to be discrete (no nonidentity 1-morphisms), then Z_1 is the center in the usual sense and Z_2 is the identity. So at this level of generality, Z_2 Z_1 is not “zero” in any sense. I assume then that you at least want to work with tensor categories, not just monoidal categories.

    In that case, should the first column really be {monoids} -> {abelian monoids}? Wouldn’t it be more appropriate to take something like {rings} -> {commutative rings}?

  8. Two comments:
    First the Kontsevich conjecture about the E_n center being E_{n+1} is a
    theorem in various contexts, see papers by Tamarkin and Hu-Kriz-Voronov (the n=1 case, the Deligne conjecture, has zillions of proofs at this point). Also in general I think it is quite formal from Jacob’s general theory (this is the idea of the Hu-Kriz-Voronov proof above, but I think the formalism makes it work very generally) — the E_n center has an E_n structure (as an internal Hom object) and a compatible E_1 structure (as endomorphisms), and together these make E_{n+1}..(see Jacob’s TFT preprint, section 4.1)

    Second, the statement that Z_2(Z_1) seems to me suspect, in that I think it’s false once you leave the discrete setting of semisimple abelian categories where Mueger’s theorem applies. In particular if you take as your algebra the monoidal oo-category D(G) of D-modules or perverse sheaves on a group, its E_1 center is D(G/G), “class sheaves” on the group. This is braided (E_2) but I don’t think it’s modular (by which let’s mean has trivial E_2 center) when G is an algebraic group (rather than a finite group) — for example the work of Boyarchenko and Drinfeld for G a unipotent group over a finite field writes this as a family of modular categories (“L-packets”) labeled by the E_2 center, which is nontrivial..

  9. To elaborate on my last comment, if G is a complex semisimple or reductive group, let D(G) be the derived (or rather oo-)category of D-modules on G with convolution – the “D-group algebra” of G. The Drinfeld center of D(G) is D(G/G) – “D-class functions”, which is E_2 (braided). However such a class function has a “central character” – you can “decompose” D-modules according to their monodromy along a torus inside G. In some (weak) sense, D(G/G) is a family of modular categories – the categories of Lusztig character sheaves – labeled by this central character, living in the dual Cartan algebra mod W.
    They correspond to extended three-dimensional TFTs (really “2 1/2 dimensional” – not defined on all 3-manifolds) called character theories which are studied in a paper of David Nadler and myself which should appear later this week. But in any case the picture is very similar to what Boyarchenko and Drinfeld have – the Drinfeld double is not itself modular, but there’s a central parameter (roughly the E_3 center) over which the theory decomposes into modular pieces. This seems to contradict the exactness idea in the homotopical setting..

  10. Regarding extending the table upwards and to the left:

    See the table at http://ncatlab.org/nlab/show/k-tuply+monoidal+n-category and the argument in the appendix to the last reference there. In particular, a 0-tuply monoidal n-category is really a *pointed* n-category. As a (-1)-category is (in the best understanding) a truth value, a 0-tuply monoidal (-1)-category is a *true* truth value, so there is only one.

    This means that the (-1)-categorial column stabilises early, but in fact you must take the pointed approach to get stabilisation to work correctly at all! As Tom Leinster (first?) pointed out, a weak 2-category (bicategory) with exactly (one object and) one morphism has a bit more structure than an abelian monoid, if you classify up to equivalence of bicategories, and there is even more structure (so *not* stabilised) in a weak 3-category with exactly one 2-morphism. But if you classify up to equivalence of *pointed* n-categories (that is, requiring equivalences and higher equivalences to preserve the basepoint in a certain sense), then you get the desired result.

    Anyway, people have been talking about whether things are pointed, so I figured that I’d better mention that.

Comments are closed.