Suppose we have a space  . There are a lot of ways to describe the cohomology of
. There are a lot of ways to describe the cohomology of  — algebraic geometers will know about étale cohomology, crystalline cohomology and (algebraic) deRham cohomology; topologists would add singular cohomology and simplicial cohomology to the list. Recently, thanks in large part to MIT’s K-theory seminar, I’ve come to understand how to tie the first three together. Each cohomology theory comes from a different way of looking at local systems.
— algebraic geometers will know about étale cohomology, crystalline cohomology and (algebraic) deRham cohomology; topologists would add singular cohomology and simplicial cohomology to the list. Recently, thanks in large part to MIT’s K-theory seminar, I’ve come to understand how to tie the first three together. Each cohomology theory comes from a different way of looking at local systems.
Roughly, a local system consists of a vector bundle  on
on  , together with some additional data which gives isomorphisms between different fibers of
, together with some additional data which gives isomorphisms between different fibers of  . In algebraic geometry, there are many different ways to make this idea precise.
. In algebraic geometry, there are many different ways to make this idea precise.
In this series of posts, I want to present several of these ideas in the case of a smooth manifold  . In each case, if you pursued the idea far enough, you would get to a major tool of modern algebraic geometry.
. In each case, if you pursued the idea far enough, you would get to a major tool of modern algebraic geometry.
I said above that a local system includes the data of isomorphisms between different fibers  and
and 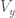 of
of  . This data can depend on the choice of a path
. This data can depend on the choice of a path  between
between  and
and 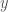 . Our three theories will be distinguished by how short the path
. Our three theories will be distinguished by how short the path  is required to be.
is required to be.
We could work with an arbitrary  . This would lead to étale sheaves
. This would lead to étale sheaves
We could work with an infinitesimal  (also known as an
(also known as an 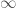 -jet). This would lead to crystals
-jet). This would lead to crystals
We could work with a  which is so small that it becomes a tangent vector. This would lead to
which is so small that it becomes a tangent vector. This would lead to 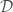 -modules
-modules
These give rise to étale cohomology, crystalline cohomology and deRham cohomology. I should point out that, for modern applications, one usually wants to work on stacks, with singularities and in arbitrary characteristic. I won’t be addressing any of those issues; I just want to give the intuition behind each theory.
In this post, I will explain how to build a cohomology theory, given a notion of local system. I will then follow up with three more posts, one for each of the specific approaches above.
As usual, this series comes with a disclaimer: These are tools that are relevant to my work, but their inner workings are not my expertise. If you want to see experts discussing this sort of thing, it looks like that conversation is going on at Urs’ journal club.
Continue reading →