Recall that the Schroeder-Bernstein theorem states that given two sets X and Y and injections f: X->Y and g:Y->X there exists a bijection h: X->Y. Probably most of our readers have proved this result at some point using the nifty ladder argument. If you haven’t seen the proof it’s covered nicely over on wikipedia (I find the “other proof” easier to follow).
My freshman year of college several of my classmates (me, Jared Weinstein, Haiwen Chu, and Mike Hill are the ones I remember) played a game of proving or disproving Schroeder-Bernstein in other categories. For example, if you have two vector spaces with linear injections both ways are they automatically isomorphic? If you have two groups with group injections both ways are they automatically isomorphic? (I don’t want to spoil your fun so I’ll put the answers to these two easy questions in comments.)
This is still a game I like to play when I run accross a new category to test my understanding. Plus it’s fun. Here are some more categories you might try (with *’s by the most interesting ones):
- Abelian groups
- Rings
- *Fields
- Topological spaces
- *Finite topological spaces
- *Vector spaces without the axiom of choice
- *Free modules over a noncommutative ring
Put proofs/counterexamples/other suggestions in comments!
Secret Blogging Seminar 
For vector spaces (with choice), injections each way means (by ordinary S-B) that the bases have the same cardinality, so they’re isomorphic.
For groups, consider the free group on 2 letters and the free group on 3 letters.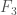
injects into 
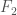sending the generators to 
(to see that this is an injection draw the right covering space). In the other direction,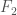 
injects into 
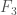in the obvious way. However, these two groups are not isomorphic because their abelianizations are not isomorphic.
The free group example suggests that the category of von Neumann algebras might be a fun place to ask this question.
Incidentally, the “other proof” you like is very similar to the Conway/Doyle proof that you can divide by 3.
Is the question for finite topological spaces actually more interesting than for topological spaces in general? Unless I’m missing something, if two sets embed in each other, then they have the same cardinality, and finiteness means the embeddings must be bijections. But since we’re talking about bijections that preserve the structure, then they have to be isomorphic. The counterexamples in the general case seem more interesting to me.
And for fields it looks fairly straightforward – a field is just an algebraic extension of a prime field, with some transcendence degree. If they both embed in each other, then the transcendence degrees must be the same (by Schroeder-Bernstein), and the prime fields must be the same, so the only question is whether the algebraic part needs to work out right, and I don’t see how that could fail. (Given any polynomial in the prime field, roots can only be permuted, so any pair of embeddings must compose to a permutation, so they must be isomorphisms.)
I’m not seeing immediately how to do the first two or last two, but I’m fairly rusty with groups and rings, and working without AC is hard.
I also believe that John Goodrick, who just got his PhD in the logic group last year, was working on a question related to this stuff (though that’s what I heard several years ago, so it may well have changed in between).
Kenny,
For fields, you can fit C(x) into a copy of C, but C(x) isn’t algebraically closed.
Suggestion: Compact manifolds without boundary, or compact manifolds rel some fixed boundary manifold.
Kenny, continuous bijections between topological spaces need not be homeomorphisms! This is why the finite case is actually interesting.
Here is what I think is a nicer proof of C-S-B than the ones I see on wikipedia (but visibly related to the first proof they give).
Let f: X –> Y, g: Y –> X be the injections. It’s enough to find a subset A of X such that g(f(A)’) = A’, where (-)’ denotes complementation (for then we define the iso by f on A and g^{-1} on A’). In other words, find a fixed point of the operator
P(X) –> P(X): A |–> g(f(A)’)’.
But this operator is clearly monotone.
Lemma: Every monotone function h: P(X) –> P(X) has a fixed point.
Proof: Let A be the intersection of the set {B in P(X): h(B) <= B}. We have h(A) <= A since h(A) <= h(B) <= B for every B in this set. But since then h(h(A)) <= h(A), h(A) is one of these B. Therefore A <= h(A) as well.
For finite topological spaces the answer is yes, they’d have to be homeomorphic. Assume you have two finite toplogical spaces with continuous injections both ways. Because the spaces are finite, both injections have to be bijections, and so their inverses gives injections betweens the topologies (i.e. between the collections of open sets of the spaces). Again by finiteness these have to be bijections. (I agree with Kenny that the question doesn’t seem to merit a *.)
For general topological spaces I remember thinking about this a while ago and coming up with this example: one space is a disjoint union of countably many points and countably many half-open intervals, the other space is the same but with open intervals. In one direction you can just map the points to the points and, lining up the half-open intervals into a countable set of countable sets, bunch up the half-opens in each set to a single open interval. In the other direction, tack the even numbered points onto endpoints of the open intervals to make them half-open, and map the odd-numbered points to all the points in the first space.
But then a friend of mine came up with a much nicer example, I think: one space is a disk with half its boundary removed, the other is an annulus with half of each boundary component removed. In one direction you can stretch the disk and wrap it around so an interval inside the piece of boundary that is removed just touches an interval inside the piece you kept. In the other direction, you can just close the hole inside the annulus by identifying the boundary half of the hole that you kept with the part you removed.
Finally, could someone explains Scott’s field injection of C(X) into C? Maybe I’m just being stupid but I don’t see it.
Unfortunately it’s not the sort of thing you see. You use one of these awful model theory results which say something like “all algebraically closed fields of characteristic 0 with cardinality the continuum are isomorphic to C.” (Warning: I’m not sure that this is the full theorem. You might need stronger hypotheses). Thus, the algebraic closure of C(X) must be isomorphic to C, but you have no hope of saying how.
On a side note, I feel like the existence of weird model theory results like this is sort of general culture that most grad students at Berkeley seem to know, but I have no idea why. Is this a side effect of me hanging out with too many model theorists, or perhaps thinking about étale topology too much (the result is important there for knowing there is an isomorphism
)?
Much of the import of the Schroder-Bernstein theorem is that it doesn’t require the axiom of choice, but nonetheless applies to the infinite case. What would interest me is when you can generalize the proof of Schroder-Bernstein, rather than just the statement.
“all algebraically closed fields of characteristic 0 with cardinality the continuum are isomorphic to C.” (Warning: I’m not sure that this is the full theorem. You might need stronger hypotheses)
No extra hypotheses needed. The theorem can be stated more generally as any two uncountable algebraically closed fields of the same characteristic and cardinality are isomorphic. The proof of the theorem doesn’t require any model theory, although it does use transfinite induction and it uses the axiom of choice in a fundamental way:
Let F and G be two fields of the same characteristic and both of uncountable cardinality lambda. Fix (f_a: a < lambda) and (g_a: a < lambda) enumerations of F and G. Now, for a < lambda we construct by induction:
i) F_a a subfield of F
ii) G_a a subfield of G and
iii) i_a and isomorphism from F_a to G_a
iv) These sequences are all extensions of previous ones
We will maintain the following inductive hypotheses:
1) f_a is in F_{a+1} and g_a is in G_{a+1}
2) F_a and G_a are algebraically closed
3) F_a and G_a are both size less than lambda (this is what makes uncountability necessary).
Then the union of the i_a’s is an isomorphism between F and G.
To construct these, let F_0 and G_0 both be the algebraicly closure of the base field. At limit steps in the induction, just take unions.
Given F_a, G_a, i_a, first we pick an extension which includes f_a. Then we pick an extension which includes g_a in exactly the same way.
If f_a is already in F_a, we don’t do anything.
If f_a is not in F_a, then it’s transcendental over F_a.
Pick so x in G which is transcendental over G_a.
This is possible because the cardinality of G is bigger than G_a.
Now extend i_a to a map from Acl(F(f_a)) to Acl(G(g_a)).
Now we have included f_a in the domain of our map.
We extend this map again to include g_a in the range in exactly the same manner. This will give us F_{a+1}, G_{a+1}, and i_{a+1} exactly as desired.
Here’s a slightly more explicit version of the field example: Let F be the algebraic closure of rational functions in countably infinitely many variables over Q, and let K be the field of rational functions in one (or indeed countably many) variables over F. The algebraic closure of K is isomorphic to F, since we can substitute our new variable(s) into the old ones, like that Hilbert hotel problem.
Greg, I’m afraid I don’t know what you mean by generalizing the proof.
For instance, a proof for vector spaces without choice (if it’s even true in that case) that commutes with the functor from Set to Vect that takes X to k[X].
For general topological spaces you can just do the closed interval and the open interval.
For finite topological spaces Omar’s argument works. I gave it a star because I hadn’t been able to come up with that argument myself (Anton found it pretty quick when I asked him though).
For fields, if you don’t like the model theory argument (which Jacob Lurie showed to us back freshman year of college) I remember that Jared and Keith Conrad managed to find an example using the field of rational functions on an elliptic curve for two different elliptic curves.
I agree with Greg that a case where you could generalize the argument would be nice, that’s exactly why I put vector spaces without choice (where it seems there’s some hope of this) on the list despite it being a rather horrible question.
Two fields (counterexample):
Let E be an elliptic curve over C, and let E –> E’ be a degree two isogeny. (In other words, E=E’/(G) where G is an order two subgroup of E.) If we choose E generically, E and E’ are not isomorphic. There is also a degree two isogeny from E’ to E: quotient E’ by the image in E’ of the 2-torsion of E. Now use the equivalence of categories between smooth algebraic curves over C and finitely generated fields of trans. degree 1 over C.
A related astonishing theorem is that an injective morphism of an algebraic variety into itself is bijective.
All right, here is a candidate counterexample for vector spaces without choice.
Let F be a field. Let V be the vector space of all functions from the integers to F. Let W be the subspace of V consisting of functions f such that f(n)=0 for n sufficiently negative. Clearly, W injects into V. Here is an injection j from V into W: For f in V, define j(f) by
j(f)(x)=0 if x< 0
j(f)(x) = f(x/2) if x>=0 and even
j(f)(x)=f( (-x-1)/2) if x>0 and odd.
I very much suspect that it is consistant with the negation of the axiom of choice that V and W are not isomorphic. Any ideas?
The answer for free modules over non-commutative rings is that the modified S-B theorem doesn’t hold.
I take my example from Lam’s “Lectures on Modules and Rings” remark 1.34. Let R=Q. This ring has the invariant basis number property (i.e. if R^n and R^m are isomorphic, then |n|=|m|). However, R^(\aleph_0) embeds in R (by the usual free-group trickery used above).
Sorry, the angled brackets around x and y disappeared in the post above. The ring R should be the free ring in two non-commmuting variables.
Here is a possible approach to showing that V and W, in my previous post, need not be isomorphic in the absence of choice:
For X any set, and F any field, let FX denote the vector space of finite linear combinations of elements of X and let F^X denote the vector space of all functions from X to F. For any vector space U, let U^* denote the vector space Hom(V,F). Clearly, (FX)^*=F^X and FX injects into (F^X)^*=(FX)^*^*. For finite X, the injection from FX into (F^X)^* is an isomorphism. I have been told that it is consistent with ZF that this map is an isomorphism for every X. (If anyone has a reference, please post it.) Let’s call that assumption the “boring duals hypothesis”, or BDH for short. If we assume choice, then BDH is not true (proof on request). This is one of the cases where adding choice makes infinite sets LESS like finite ones.
So, with V and W as in my previous post, the BDH says that V^* =FZ, in other words, that V^* has a countable basis. If V were isomorphic to W, then W^* would also have to have a countable basis. But W injects into W^*, because there is a perfect pairing on W given by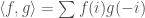
, and it is easy to show that W does not have a countable basis.
So, the question: Without choice, is it true that a subspace of a vector space with a countable basis must, itself, have a countable (or finite) basis? (If it will make the argument simpler, you may assume that F is finite.) I think that this is true, because I think that the standard row-echelon proof doesn’t make any choices. If so, we have a contradiction and hence a counterexample.
I’m confused. How do you show that W doesn’t have a countable basis without choice?
If F is countable, then very easily — if V is a vector space with countable basis (b_1, b_2, b_3, …) over a countable field F then V is countable. (First, list 0, then list all nonzero multiples of b_1, then list all nonzero combinations of b_1 and b_2 where the coefficient of b_2 is nonzero, and so forth.) W, on the other hand, is not countable. (For every subset of the positive integer, the characteristic function of that subset is in W.)
I have a candidate argument which doesn’t look at the cardinality of F, but it is a bit long so I am going to hold off including it unless you want it.
Here is an explicit, uncountable, linearly independent subset of W. Take a bijection f between the positive integers and the rationals. (Does not require choice.) For every real number r, consider the characteristic function of f^{-1}([-\infty, r]).
So, we just need to know that a vector space with a countable basis can not contain an uncountable, linearly independent, subset.
I’m confused, if the field is countable aren’t you just saying “we just need to show that a vector space of countable cardinality can not contain an subspace of uncountable cardinality” which is clear? I’m sure I’m missing something.
No, you are right. I just came up with a messier argument, but that works so we are done.
The argument in summary: Work over a countable field. Notice the injections from V into W and W into V. Assume (for contradiction) that V is isomorphic to W. Then V^* is isomorphic to W^*. By the BDH, V^* has a countable basis, and therefore is countable itself. But W, which is uncountable, injects into W^* by the pairing in comment 19. Contradiction.
One of the counterintuitive things about vector spaces without choice is that given an injection f: W->V, the dual map f^*: V^*->W^* need not be a surjection! In fact, in David’s example W injects into V, but V^* has countable cardinality while W^* has uncountable cardinality. So f^* is not a surjection!
David,
My understanding is that when one removes the axiom of choice, there are cardinalities which are simply incomparable. So one must be careful when talking about “uncountable” (does this mean incomparable with denumerable sets, or does it mean strictly greater than a denumerable set).
So I would also mention the following easy facts. First, BDH is compatible with SB (that is as long as BDH is compatible with ZF, since SB follows from ZF even without choice). Second, Q and R are definable in ZF (again easy) with Q countable and R of strictly larger cardinality.
I was just talking with Noah about this, and we seem to have come up with something interesting, though it doesn’t quite confirm David’s thought that BDH is compatible with ZF. We’ll try to prove a special case of BDH from the assumption that there are no non-principal ultrafilters on Z – I’m fairly sure that this is consistent with ZF, because I think it’s just the negation of the boolean prime ideal theorem, which I know is independent of ZF (even though it’s weaker than full choice).
Let’s consider the special case where F=2 (that is, the field of two elements). Then 2Z can be identified with the set of finite subsets of Z. 2^Z can be identified with the set of all subsets of Z, where addition is done by symmetric differents (that is, S+T is the set of all elements that are in exactly one of S and T). Now, a linear function from 2^Z to 2 is a partitioning of 2^Z, such that one side (the sets sent to 0) is closed under addition. The natural embedding of 2Z into the space of such functions sends any finite set S to the collection of all subsets whose intersection with S has even cardinality (weird, huh?).
Now the question is whether there are any other such partitions, where one side is additive-closed and the other side is additive-non-closed. If there were a non-principal ultrafilter on Z, then we would have such a partition – a function that takes elements of the ultrafilter to 1 and non-elements (that is, elements of the complementary maximal ideal) to 0 would be a ring homomorphism from the boolean algebra 2^Z to 2, and would thus a fortiori be a linear map from 2^Z to 2.
But as we saw above, there are in fact linear maps that are not ring homomorphisms – if S is a two element set, then the corresponding function sends two distinct singletons each to 1, and sends their intersection to 0.
So somehow, we would like to prove that if there are no non-principal ultrafilters on Z, then there are no linear maps other than the ones that send a set to 0 iff it contains evenly many elements from some fixed finite set S.
(The situation for other finite fields is similar, but more complicated – an element of FZ where F has prime cardinality is a finite set where each element has some multiplicity less than the prime; the corresponding maps send a set to the sum of the multiplicities of the elements of this set that it contains. I don’t think this naturally suggests a connection to ultrafilters or anything.)
Another question this raises then is whether the Schroeder-Bernstein theorem for fields follows from the prime ideal theorem, or whether it requires the full strength of AC.
The last paragraph there should be asking about S-B for vector spaces of course, not fields, since there are counterexamples for fields above.
And now I see my mistake about fields from earlier – I was thinking of the result stating that algebraically closed fields are determined up to isomorphism by two numbers (their characteristic and their transcendence degree) and thought that this generalized to fields that weren’t necessarily algebraically closed. So S-B is true for algebraically closed fields, but not true for fields in general, because you can embed an algebraically closed field in a non-algebraically closed subfield, as in the example of C and rational functions in one variable over C.
Reading Noah Snyder’s comment (#13), I realized that I gave very complicated examples for general topological spaces: what happened was that when I thought about this years ago, I realized that continuous injections both ways are easy (Noah’s example of open and closed intervals are the simplest example, probably), and so I looked for non-homeomorphic spaces with continuous bijections both ways.
My feeling is that without choice, there’s no reason at all to expect that the ultrafilters generate all of the dual of 2^Z. Indeed, that statement feels very much like a variant of the Krein-Milman theorem, which requires choice (the analogous statement that follows from Krein-Milman is that the positive part of the unit ball of the dual of l^\infty is the weak* closed convex hull of the ultrafilters, though since the principal ultrafilters are actually dense in all the ultrafilters, this isn’t really an interesting statement). However, wikipedia seems to indicate that Krein-Milman is consistent with the negation of BPIT, so I would expect that it’s consistent that there are no nonprincipal ultrafilters on Z but every element in the dual of 2^Z has to be a linear combination of ultrafilters.
Hmmm, I take that back. What Krein-Milman would suggest is that the span of the ultrafilters is dense in (2^Z)* (in the natural product topology), but it’s already easy to tell that the span of the principal ultrafilters is dense. And looking at it that way, it seems more plausible that the non-existence of nonprincipal ultrafilters would imply the dual is just spanned by the principal ultrafilters.
New here, have a question. When you say that F_3 injects in F_2 under the given map it’s said that to see injectivity draw the right covering space. Could you elaborate? Can’t injectivity be shown directly?
Since no one responded to Josh’s question, I’ll go ahead. In fact, we can inject a free group with countably many generators in F_2; the easiest way to see this is to use elementary covering space theory, as Noah said (the fundamental group functor applied to a covering projection embeds the fundamental group of the total space into the fundamental group of the base space). Take the base space to be a figure 8, and the total space to be a helix with a circle attached every 360 degrees, with a hopefully obvious covering projection. Since the total space is homotopy equivalent to a countable bouquet of circles, its fundamental group is a free group on countably many generators (using van Kampen or something else), and there you have it.
Algebraically, this corresponds to taking the subgroup of the free group F(x, y) generated by the elements x^{-n}yx^n where n ranges over the integers. This is a free group generated by these elements (i.e., there are no nontrivial relations).
There are purely algebraic ways to establish such injections, but they are notoriously harder than the route via covering space theory (what’s that called? Schreier-Nielsen theory?).