Mike Freedman on SPC4

Mike Freedman gave a talk last week at Berkeley titled “(Still) thinking about the smooth 4-dimensional Poincare conjecture”, and I’d like to try and relate the main idea.

Back in 2009 Mike, Bob Gompf, Kevin Walker and I wrote a paper “Man and machine thinking about the smooth 4-dimensional Poincare conjecture”, in which we discussed various equivalent and stronger conjectures with more of a “three manifold flavour”, as well as proposing a way to show that certain potential counterexamples, the Cappell-Shaneson spheres, really were counterexamples, using Khovanov homology.

As it turned out, for the Cappell-Shaneson spheres that our computers could cope with Khovanov homology didn’t provide an obstruction. Shortly thereafter, Selman Akbulut posted a short paper showing that a certain integer family of CS spheres (including the two examples we considered) were all in fact standard, and not long after that Bob Gompf killed off some more. In fact, there’s been a whole flurry of work on SPC4 recently: Nash proposing some more counterexamples, Akbulut killing these off too, Akbulut proving a very general class of 4-spheres are standard, along with [1], [2] and [3]. There’s also a paper on Property 2R by Gompf, Scharlemann and Thompson.

Even though recent progress means that there are far far fewer potential counterexamples to SPC4 available, Mike has come up with another idea for detecting counterexamples! Essentially, from each proposed counterexample to the Andrews-Curtis conjecture (below), one can produce a homotopy 4-spheres. This part of the story is old news, but I’ll go over it carefully below. Mike points out that this construction also provides a family of embedded homology 3-spheres. Now any 3-manifold embeds in S^5, but not every 3-manifold embeds in S^4 (e.g. lens spaces, but see more below). The hope now is to show that one of these homology 3-spheres can not embed in the standard S^4, and thus that the homotopy 4-sphere it sits in must be exotic. Mike gave a condition on a 3-manifold Y that exactly determines whether it embeds in S^4, and talked about his ideas towards making this condition an effective test.

So, what is the Andrews-Curtis conjecture? A balanced presentation of a group is simply a presentation with equal numbers of generators and relations. The Andrews-Curtis moves on a balanced presentation are

  • “1-handle slides”: replace a pair of generators \{x, y\} by \{x, xy\}.
  • “2-handle slides”: replace a pair of relations \{r, s\} by \{g r g^{-1} s, s\} (here g is any word in the generators).
  • “handle cancellation”: add a generator along with a new relation killing it

The Andrews-Curtis conjecture says that any balanced presentation of the trivial group can be transformed by Andrews-Curtis moves to the trivial presentation. (There’s a stronger version that says handle cancellation isn’t even needed.) Despite the name, it’s widely expected to be false.

Before continuing, I should explain the funny names I’ve given the moves. Given any presentation of a group, we can build a two-complex whose fundamental group is the group: just take some 1-handles for the generators, and attach 2-handles killing the relations. The names I’ve given the moves correspond to the appropriate geometric operations on this 2-complex.

As an example, consider the presentation xyx=yxy, x^5 = y^4. It’s easy to check that this is the trivial group: y = x^{-1}y^{-1}xyx, so y^5 = x^{-1}y^{-1}x^5yx = x^{-1}y^4x = x^5. Thus y^5 = y^4, and y=1. Even though that was easy, no one has found a sequence of Andrews-Curtis move, even after having looked extremely hard! (e.g. this paper) This is just one case of the family \{ xyx=yxy, x^{n+1} = y^n \} of proposed counterexamples that appears in the paper “A potential smooth counterexample in dimension 4 to the Poincaré conjecture, the Schoenflies conjecture, and the Andrews-Curtis conjecture”, by Selman Akbulut and Rob Kirby (Topology 24 (1985), 375–390). So far the Andrews-Curtis conjecture is just a problem in group theory, but the title of that paper should clue you in that we’re about to construct some manifolds!

Given a balanced presentation P, we can build a 5-manifold Q(P)—just like we built the 2-complex above, start with a 5-ball, attach some 5-dimensional 1-handles for the generators, and then attach some 5-dimensional 2-handles for the relations. To attach the two handles, we actually need to pick links in the boundary of the 0- and 1-handles representing in \pi_1 the relation, but since these boundaries are 4-dimensional there are actually no choices to make. If we started with a presentation of the trivial group, then \partial Q(P) is a homotopy 4-sphere. Moreover, if the presentation is a counterexample to the Andrews-Curtis conjecture, then perhaps this homotopy 4-sphere is a good candidate counterexample to SPC4: you can’t make it standard just by handle slides corresponding to some Andrews-Curtis moves! Of course, you have more freedom to simplify presentations of 4-manifolds, so just having a counterexample to AC doesn’t ensure a counterexample to SPC4.

As it turns out, Bob Gompf subsequently showed that \partial Q(xyx=yxy, x^5 = y^4) is in fact the standard 4-sphere (by introducing a cancelling pair of 2- and 3-handles!). Nevertheless all the higher values of n are still open.

We can alternatively build \partial Q(P) in a different way. Start with a 4-ball, attached some 4-dimensional 1-handles for the generators, and now pick some links L realizing the relations, and attach 4-dimensional 2-handles along these. This produces a 4-manifold W(P,L), which genuinely depends on L, but whose double (the boundary of W \times I) is just our homotopy 4-sphere \partial Q(P). This way of building the homotopy 4-sphere gives us something extra; a 3-manifold Y(P, L) = \partial W(P, L) \times \{1/2\} sitting inside \partial Q(P). In fact, this 3-manifold is a homology sphere.

The challenge now is to pick some counterexample to the AC conjecture, along with a corresponding link, and then to prove that the resulting homology sphere can not be embedded in the standard 4-sphere.

Now Mike wasn’t claiming he knew how to do this; but he did explain a relatively easy theorem giving a precise characterization of when a 3-manifold embeds in the standard 4-sphere, which has a very “3-manifold flavour”. This was

Theorem. A 3-manifold Y embeds in S^4 if and only if it has an Heegaard diagram (\Sigma, \alpha, \beta) and an embedding \iota: \Sigma \to R^3, such that \iota(\alpha) is an unlink, and \iota(\beta) is an unlink.

Mike calls this a doubly unlinked embedded Heegaard diagram. The proof of this theorem is via ambient Morse theory, but I won’t try to give the details here. In fact, every homology 3-sphere has an embedded Heegaard diagram which is doubly null, meaning that the linking matrices for \iota(\alpha) and \iota(\beta) vanish. Of course, actually using this theorem to show that Y doesn’t embed would involve a lot of work. It seems that we’d need to consider all possible embeddings of \Sigma, as well as all possible systems of curves \alpha and \beta. I think Mike has some ideas about this (if you go “far out in the mapping class group”, it should be impossible that the images of the curves are unlinked), but I don’t think I could reproduce those ideas usefully here. Perhaps some of our readers can comment on how plausible this seems, and maybe if we’re lucky Mike will turn up too and say some more.

15 thoughts on “Mike Freedman on SPC4”

  1. Cool!

    Six or seven months ago (still) thinking about SPC4, I wrote some memory bound C++ code that tried to prove any balanced presentation of the trivial group can be transformed by Andrews-Curtis moves to the trivial presentation. I mainly looked at the Akbulut-Kirby family of balanced presentations.

    I was going to change the algorithm to make it parallel and CPU bound, then port it to the CUDA. But, as problem size grew exponentially with the Akbulut-Kirby family of balanced presentations, I never got around to doing it, as it seemed fruitless. (The C++ code was gobbling up memory.)

    Freedman’s talk and your post now give me some renewed motivation to parallelize the algorithm, make CPU bound, and port it to the CUDA. Thanks!

    PS: Did anyone write up notes for the talk? It’d be nice to see the details.

  2. Let me just mention that I heard about this Andrews-Curtis construction in graduate school from Andrew Casson. Mike Freedman makes a very good point (as he often does), but this particular point is conventional wisdom among some of the veteran 4-manifold topologists.

  3. Hi Greg,

    I’d meant to put the emphasis on the idea of using this obstruction for a homology sphere embedding in the standard S^4, rather than just the construction of a homotopy 4-sphere. Mike certainly did this in his talk; I reversed the order of presentation here, but maybe it was misleading.

  5. In the statement of the theorem, I take it there’s no restriction on the image of the surface in R^3? Thus conceivably it could be highly knotted, though it’s hard to see how using such an embedding is helpful…

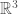  6. Nathan, though I haven’t thought about it in great detail, I’d guess the freedom in choosing the embedding \iota can be useful in that it may allow one freedom to create unlinks \iota(\alpha) and \iota(\beta) in \mathbb{R}^3.

  7. @Nathan, @Kelly, so one of the first challenges is to show that for a sufficiently knotted embedding, at least one of the links \iota(\alpha) and \iota(\beta) is linked.

    There’s also the result that a homology sphere always have an embedded Heegaard diagram which is “doubly null”, so that the two linking matrices are zero (i.e. any linking is only detected by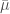 \bar{\mu}-invariants or worse). I don’t really have any sense of how knotted these embeddings might be.

  9. Anyone have some spare time on a compute cluster they’d like to donate to the Andrews-Curtis conjecture? Instead of rewriting my C++ code using CUDA I’ve used boost::mpi. Now, all I need is a cluster to run it on. If there are no takers, I’ll just use an EC2’s HPC cluster.

  10. @Kelly, next year hopefully I’ll have easy access to the big computer at ANU. In the meantime I have a single 8-core machine that’s often available, but EC2 is probably your best bet.

  11. @Scott, thanks. I guess I’ll just run it on EC2 HPC nodes. So, in the next week or so I should be able to say more on the Akbulut-Kirby family of balanced presentations, fingers crossed. I’ll keep you posted.

  13. In the battle of Andrews-Curtis vs EC2 the winner is Andrews-Curtis.

    I’d hoped to find the derivation, using Andrews-Curtis moves, of the triviality of the $n=4$ member of Akbulut and Kirby family of balanced presentations. However, the exponential growth of the derivation tree overwhelms the cluster.

    More to the point, when applying Andrews-Curtis moves to the $n=4$ member of the Akbulut and Kirby family one often obtains the same balanced presentation many times. To prevent the search from going into infinite loops one has to keep around the set of previously seen balanced presentations and discard each new balanced presentation that is in this set. Keeping around this set of previously seen balanced presentations then becomes the problem, as one quickly runs out of memory.

    To counter this one tries to make each balanced presentation as small as possible. I do this by sharing relators among balanced presentations. (In other words, If two balanced presentations have the same relator $aba=bab$, say, then the two balanced presentations each point to a single instance of this relator.) I save some more memory by storing the balanced presentations and relators in intrusive binary trees. (This eliminates lots of overhead associated with a non-intrusive binary trees, but it still has overhead of its own, two pointers per relator and two pointers per balanced presentation.) Also, I make each relator as small as possible. (I do this by having each generator represented by a bit pattern: 100 for $a$, 010 for $b$, 011 for $a^{-1}$, and 101 for $b^{-1}$. I use boost’s dynamic_bitset to manage these arrays of bits.) Furthermore, each balanced presentation is associated with a single node in the cluster where the balanced presentation is stored in memory. Thus, the memory limit for comes from the total memory of the cluster and not from the memory of any one node.

    Even with all of this, the exponential growth of the derivation tree is to fast to say anything about the $n=4$ member of the Akbulut and Kirby family.

    For example the total number of balanced presentations stored for $n=4$ grows as follows:

    -At level 0 there is 1 unique balanced presentation
    -At level 1 there are 13 unique balanced presentations
    -At level 2 there are 114 unique balanced presentations
    -At level 3 there are 899 unique balanced presentations
    -At level 4 there are 6838 unique balanced presentations
    -At level 5 there are 51197 unique balanced presentations
    -At level 6 there are 380248 unique balanced presentations
    -At level 7 there are 2811754 unique balanced presentations
    -At level 8 there are 20739470 unique balanced presentations
    -At level 9 there are 152751494 unique balanced presentations

    So, a basic rule of thumb is that each new level requires about 8-9 times the number of servers used to obtain the previous level.

    To give a feel for what this means I’ll give an example. To go to level 9 I used 16 nodes each with 23GB of RAM, in total 369GB. When it reached level 9 about 40 percent of the memory was used and the average length of a balanced presentation was about 84 generators.

    Thus, to go to level 20, which is around the beginning of the unexplored region for $n=4$, would require about 2470 EB. The Cisco Visual Networking Index IP traffic forecast predicts that by 2013 annual global IP traffic will reach 667 EB. So, going to level 20 would require about 3.7 times that much RAM!

    As you can see, in the battle of Andrews-Curtis vs EC2 the winner is Andrews-Curtis by a knock-out.

  15. For those counting at home, I used the same Andrews-Curtis moves presented in the Havas and Ramsay paper, doi 10.1142/S0218196703001365; so, the number of balanced presentations at a given level should be reckoned with respect to these moves.

Comments are closed.