Dear Internets,
I’m sorry for having disappeared for so long, and I promise I’ll get back to my series on planar algebras soon. I’ve been busy writing papers and couldn’t really justify to my coauthors why I’m not writing our papers and instead writing math on the internet. However, Saturday I was in San Francisco without access to LaTeX, and Malia was at her spinning guild, so here’s a post!
Yours,
Noah
P.S. Below the break I’ll walk you through understanding much of the representation theory of the small quantum group for at a third root of unity, assuming you already understand the representation theory of the usual lie algebra
. It’s an interesting example to work through because the representation theory is not semisimple. There will be lots of fun pictures. The choice of a third root of unity isn’t important here, everything would work similarly for any odd root of unity.
Consider the small quantum group at a third root of unity. That is, let
be a primitive third root of unity and consider the algebra (over the complex numbers) with generators
,
, and
and the following relations:
The nicest representation of this algebra is the two dimensional defining representation (so called because it has highest weight
). It is spanned by
with the action give by:
,
,
,
As usual with the representation theory of -like objects we draw this representation using raising and lowering operators like this:
Now that we have one representation we can try taking tensor powers of it and decomposing (for this you need to use the usual Hopf algebra structure). The tensor square breaks up the way you’d expect as the trivial representation ad the three-dimensional representation
. Here are the pictures for these representations
It’s not hard to see, using the usual highest-weight yoga, that these three represetations are the only finite dimensional irreducible representations of the small quantum group. In the classical case we can use the action of the Casimir element to distinguish these three representations and show that they lie in different blocks (that is there are no extensions between them). However, in the small quantum group case the quantum casimir element acts by 2 on
but acts by -1 on both
and
. Thus there could be extensions between
and
. In fact there are, for example the baby Verma module
:
However, instead of trying to understand all representations, instead let’s just try to understand the representations that occur as summands of tensor products of the irreducible representations.
So, we take the tensor product . From the classical case we would expect to get
, however instead we have a single six-dimensional indecomposable representation (note that when there are two arrows with the same label coming out of a dot that means that the vector is sent to a linear combination of two other vectors):

What do the four “weight spaces” going left-to-right mean? After all, only has three possible eigenvalues (
). Nonetheless the small quantum group is naturally graded, and since
was a graded module, every tensor power of it will also be. So even though the highest weight-space on the right and the lowest one on the left both have
acting by
, it still makes sense to draw the picture the way I’ve drawn it.
As you can see this representation, which we’ll call (because it is the restriction of a tilting module) is rather complicated. It has a 2-dimensional submodule isomorphic to
, at the next layer (that is after modding out by the 2-dimensional subrepresentation) there are two trivial representations. Finally at the top level there’s another copy of the 2-dimensional irrep.
Ok, let’s keep going, let’s take the tensor product . This is a 12-dimensional representation. From the classical case we would expect to see
. The two copies of
do occur as summands (they have to as their block is semi-simple) but instead of
and
you instead find the following indecomposable representation
:
Now it turns out that . So at this point the process stops and we’ve found all indecomposible representations which are summands of tensor powers of standard representation.
Okay, what’s left to understand about this category of representations? We know that the objects are . We know some of the tensor product rules, and the rest aren’t too difficult to work out. For example, in the Grothendiek group:
But since these representations are indecomposable instead of irreducible, we should also understand what their hom spaces look like. That’s also not so hard to work out, the only maps are the zero maps, the identity maps, and the following additional maps:
- The quotient map from T_3 to V_1
- The inclusion map from V_1 to T_3
- The map from T_3 to itself gotten by composing the previous two maps
- The quotient map from T_4 to V_0
- The inclusion map from V_0 to T_4
- The map from T_4 to iself gotten by composing the previous two maps
- Two strange maps from T_4 to T_3 sending each of the three-dimensional quotients of T_4 (which is either a Verma module or a dual Verma module) to the corresponding subrepresentation of T_3
- Two similar strange maps from T_3 to T_4





Great workout. Just noticed a typo in the defining relations. Shouldn’t it be ?
?
Fixed, thanks!
I like this sort of small example thing. I was unaware that the cyclic reps weren’t tensor generated by V_1, but your remark about grading makes it kind of obvious.
More corrections:
“It has a 2-dimensional submodule isomorphic to V_2,” should have V_1.
Is there a way to change the spelling in the title?
Well, you should be a bit careful what you mean by “tensor generated.” Here I’ve taken tensor products, direct sums, and direct summands. Often when people say “tensor generated” they also allow subobjects and quotient objects, in which case you get a much larger category here.
By the way, Scott, you have the bits to change typos in other people’s posts yourself.
You had the tensor product wrong; those
wrong; those 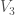 s should I think be
s should I think be  . I’ve changed it above.
. I’ve changed it above.
Also, your calculation
in the Grothendieck group was incorrect; you forgot the two copies of in
in  .
.