Here’s a basic example that comes up if you work with elliptic curves: Let  be a prime which is
be a prime which is 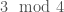 . Let
. Let 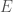 be the elliptic curve
be the elliptic curve 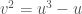 over a field of characteristic
over a field of characteristic  . Then
. Then 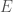 has an endomorphism
has an endomorphism 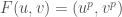 . It turns out that, in the group law on
. It turns out that, in the group law on 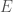 , we have
, we have ![F^2 = [-p]](https://s0.wp.com/latex.php?latex=F%5E2+%3D+%5B-p%5D&bg=ffffff&fg=444444&s=0&c=20201002) . That is to say,
. That is to say,  plus
plus  copies of
copies of 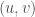 is trivial.
is trivial.
I remember when I learned this trying to check it by hand, and being astonished at how out of reach the computation was. There are nice proofs using higher theory, but shouldn’t you just be able to write down an equation which had a pole at  and vanished to order
and vanished to order  at
at 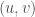 ?
?
There is a nice way to check the prime 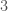 by hand. I’ll use
by hand. I’ll use  for equivalence in the group law of
for equivalence in the group law of 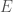 . Remember that the group law on
. Remember that the group law on 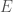 has
has 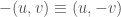 and has
and has  whenever
whenever 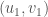 ,
, 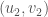 and
and 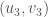 are collinear.
are collinear.
We first show that
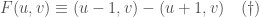
Proof of 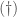 : We want to show that
: We want to show that 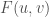 ,
, 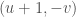 and
and 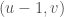 add up to zero in the group law of
add up to zero in the group law of  . In other words, we want to show that these points are collinear. We just check:
. In other words, we want to show that these points are collinear. We just check:
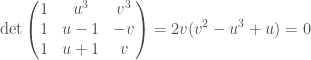
as desired.  .
.
Use of  : Let
: Let  be a point on
be a point on 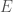 . Applying
. Applying 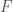 twice, we get
twice, we get
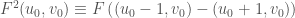
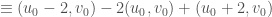 .
.
Now, the horizontal line  crosses
crosses 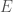 at three points:
at three points: 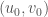 ,
, 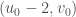 and
and 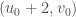 . (Of course,
. (Of course, 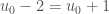 , since we are in characteristic three.) So
, since we are in characteristic three.) So 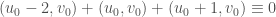 and we have
and we have

as desired.  .
.
I was reminded of this last year when Jared Weinstein visited Michigan and told me a stronger statement: In the Jacobian of  , we have
, we have ![F^2 = [(-1)^{(p-1)/2} p]](https://s0.wp.com/latex.php?latex=F%5E2+%3D+%5B%28-1%29%5E%7B%28p-1%29%2F2%7D+p%5D&bg=ffffff&fg=444444&s=0&c=20201002) , where
, where 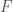 is once again the automorphism
is once again the automorphism 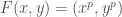 .
.
Let me first note why this is related to the discussion of the elliptic curve above. (Please don’t run away just because that sentence contained the word Jacobian! It’s really a very concrete thing. I’ll explain more below.) Letting 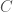 be the curve
be the curve  , and letting
, and letting  be
be 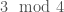 , we have a map
, we have a map 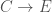 sending
sending 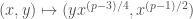 , and this map commutes with
, and this map commutes with 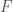 . I’m going to gloss over why checking
. I’m going to gloss over why checking ![F^2 = [(-1)^{(p-1)/2} p]](https://s0.wp.com/latex.php?latex=F%5E2+%3D+%5B%28-1%29%5E%7B%28p-1%29%2F2%7D+p%5D&bg=ffffff&fg=444444&s=0&c=20201002) on
on 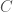 will also check it on
will also check it on 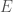 , because I want to get on to playing with the curve
, because I want to get on to playing with the curve 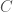 , but it does.
, but it does.
So, after talking to Jared, I was really curious why 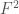 acted so nicely on the Jacobian of
acted so nicely on the Jacobian of 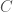 . There are some nice conceptual proofs but, again, I wanted to actually see it. Now I do.
. There are some nice conceptual proofs but, again, I wanted to actually see it. Now I do.
Continue reading →